培養學生逆向思維的幾點做法

陳瑞

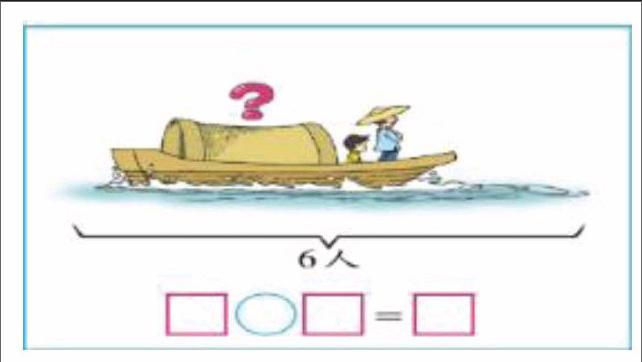
當解決問題感到繁復時，如果轉到逆向來考慮，往往可以得到令人滿意的效果，這就是一種逆向思維。對于逆向思維小學生并不陌生，從一年級開始，教材上就有了這種方法的滲透，如圖：

船上共有6人，在棚外有2人，棚內有幾人？對于這道題目，老師想得到的列式是6-2=4，即根據數量關系：總人數一棚外人數=棚內人數。而學生在列式時大部分學生卻列成了2+4=6，可以看出學生實際上就運用了2+（？）=6的逆向思維方式。在小學數學教學中，重視對學生進行這種逆向思維的訓練，有利于加速學生思維能力的提高，有利于學生數學素質的提高，有利于創新能力的培養。下面結合自己的教學經驗對如何培養學生的逆向思維談四點不成熟的建議：

一、加強概念的反向應用訓練

數學中的許多概念來源于問題或問題本身存在著的互逆關系，這些都是培養學生逆向思維的極好素材。例如：在教學三角形內角和時，有很多同學對這個問題很困惑：“一個三角形中，至少有一個內角大于或等于60度”。我是這樣給學生解釋的：假定三角形中沒有角大于或等于60度，則這個三角形所有的內角都小于60度，那么這個三角形的內角和就小于180度，這與三角形內角和為180度相矛盾，說明“假定三角形中沒有角大于或等于60度”是錯誤的，所以原結論是正確的。一個從順向很難解決的問題，如果從逆向考慮的話，輕而易舉地解決了。再如：一個兩位小數用“四舍五入”法截取的近似值為5.8，原數最大是（）。以前，我們是給一些精確數根據需要用四舍五入法求近似值，這道題根據已經截取的近似值5.8求原數，我們可以逆過來思考，先確定原數的范圍，在5.75與5.84之間，從而得原數最大是5.84。像這樣每當接觸一個新概念時，如果注意其反向訓練，不僅能使學生準確理解這些概念，巧妙求解有關問題，還能培養他們養成進行逆向思維的習慣。

二、注重公式逆運用

數學中的公式都具有雙向性，而學生往往只習慣于從左往右地運用公式，缺乏逆向思維的自覺性和基本功。顯然，這對于學生數學能力的提高是相當不利的。在正向應用的同時，加強公式的逆向應用訓練，不僅可以加深學生對公式的理解和掌握，培養學生靈活運用公式的能力，還可以培養學生的雙向思維能力。例如：學習乘法分配律后，經常讓學生練習形如：“38×23+62×23”的題目，加深對乘法分配律的理解；再如：學習三角形面積計算公式后，設計這樣一道練習：一個三角形的面積是32平方厘米，底長8厘米，這個底邊上的高長多少厘米？這就需要學生對三角形面積公式“三角形面積=底×高÷2”轉換成式子“高=三角形的面積÷底×2”來進行計算。在教學中注重對公式的逆運用，久而久之，往往能收到出奇制勝的效果。

三、加強互逆運算的轉化訓練

任何一個順向問題都可以轉化成逆向問題，而且問題的條件越多，改變成逆向問題的數量就越多。如：學校原有56位教師，暑假期間調走6位教師，又調來5位教師，學校現在有多少位教師？這是一道簡單的兩步應用題，按照順向數量關系列式為56-6+5=（）。這道題可以轉化為三種逆向題：①學校現在有55位教師，在暑假期間調走6位教師，又調來5位教師，學校原有多少位教師？②學校原有56位教師，暑假期間調走6位教師，現在學校有55位教師，請問調來多少位教師？③學校原有56位教師，暑假期間調來5位教師，現在學校有55位教師，請問調走多少位教師？改編的三道題的數量關系表面上看來與原題是一樣的，但在具體解答過程中，它們的數量關系發生了逆轉變化。教學時可以將順向問題轉化為逆向問題，幫助學生實現由順向到逆向思維方向的重新建立，進而發展學生的逆向思考能力。

四、注重在教學中舉反例的訓練

用來證明某個問題（或命題）不成立的例子，叫作反例。B·R·蓋爾鮑姆曾說：“數學有兩大類——證明和構造反例。……一個數學問題用一個反例予以解決，給人的刺激猶如一出好劇。”由于“反例”在否定一個命題時具有特殊的威力，因此學習中適當應用反例，可以收到事半功倍之效。例如：命題“一個數的倒數一定比它本身小”，只要舉一個例子：“1的倒數是1，等于它本身”，就可以證明命題是錯誤的。學生舉反例對于知識的領會、記憶、加深理解以及判斷錯誤命題都有較大作用。

在小學數學教學中，培養學生的逆向思維能力是一項長期而艱巨的工作，教師要有意識有步驟地培養和訓練。相信只要學生掌握了這種思維方式，他們考慮問題時的思路會更開闊，思維會更活躍。教師應適時組織學生進行先順后逆的思維訓練，這對于培養學生思維的自覺性是大有裨益的。endprint