一種具備干擾臺站剔除的多臺站定位方法

朱夏樂

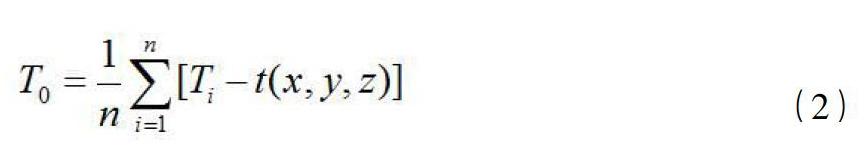
摘要：在地震預警技術中震中的精確定位是一個難點問題，相較于僅利用單臺P波記錄進行震中定位，多臺站地震定位具備更高的精度。然而，在多臺定位中，存在由于某一臺站誤觸發導致整體地震定位結果誤差過大的問題。本文在基于網格搜索的多臺定位基礎上，利用Delaunay三角剖分對可能為干擾觸發的臺站進行剔除。通過實際天然地震定位對本文提出的方法進行驗證，采用了Delaunay三角剖分可以有效剔除誤觸發多臺站，在工程應用中有實際應用價值。

Abstract： Accurate location of epicenter is a difficult problem in earthquake early-warning technology. Compared with single P wave record， multiple stations have higher accuracy. However， there is a problem of large error in overall seismic positioning results due to the mistrigger of one station. In this paper， based on grid search， Delaunay triangulation is used to eliminate stations that may be interference triggered. The method proposed in this paper is verified by the actual natural seismic positioning， and the Delaunay triangulation can be used to effectively eliminate multiple mis-triggered stations， which has practical application value in engineering applications.

關鍵詞：地震預警;干擾波;誤觸發

Key words： earthquake early warning;interference wave;triggered by mistake

中圖分類號：P315.73? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1006-4311（2018）35-0249-03

0? 引言

在假設地震波速度已知且地下為各向同性介質的前提下，通過地面地震監測點臺站布設位置的分布情況，可以計算得到地下任一點到地面監測點之間的地震波旅行時。因此，當有地震發生時比對各臺站之間的到時差與地下離散模型地震波旅行時之間的差值，差值絕對值最小的點即為地震的震中位置。然而，若在此時某一臺站出現了誤觸發，則會獲得錯誤的臺站到時差，對地震定位的結果會有極大的影響。因此，在多臺站地震定位中剔除干擾觸發臺站，對于地震定位的準確性具有至關重要的作用。

1? 方法原理

多臺網格搜索定位法首先建立目標區域的理論網格化走時到時差，并結合地下波速模型，以任意網格單元作為震源，計算各臺站兩兩之間臺站的P波到時差。地震發生時，依據臺站之間實際的到時差，與計算的時差目錄作對比，快速查找出到時差最接近的網格單元，震中就限定在該網格中。該方法采用求取目標函數最小值方法來進行地震定位，即在全區域內找到一個網格單元EP（x，y，z，t），使下式取最小值：

其中，Tj，tj為j號臺站的觀測到時和理論走時;Ti，ti為i號臺站的觀測到時和理論走時;（x，y，z）代表震源位置;n為已觸發臺站數量。根據最小二乘原理，使函數F取最小值的網格即為震源所處位置。

發震時刻T0的計算則由各臺站到時減去各臺站的理論走時后，累加求其平均，如下式所示：

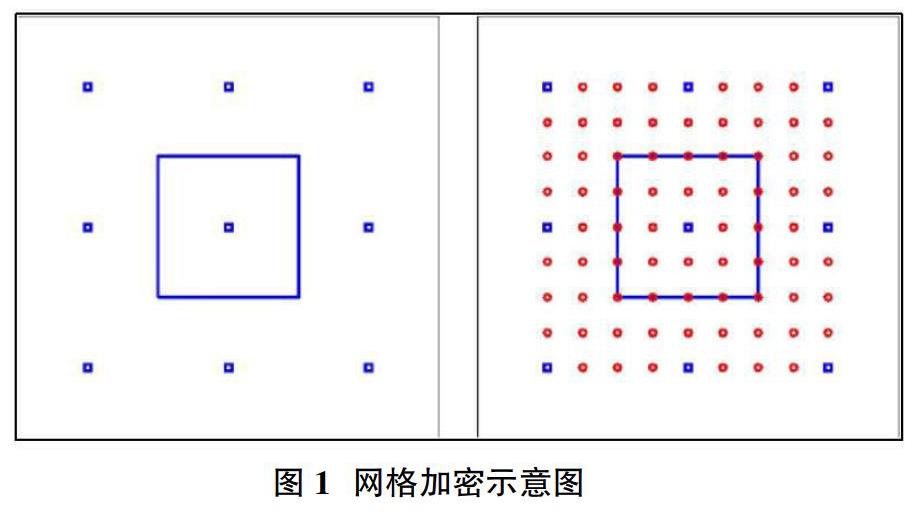
為了更加精確和快速的定位震中，在第一次定位震中時，往往選定一個較大的網格間距，地震定位在某一網格后，再將該網格剖分成小網格，進行二次搜索，逐步縮小網格間距，就可得到滿足精度要求的震源位置。根據上述定位過程可知，在目標區域較大時，在相同的定位精度下，該方法耗時少。

圖1為加密網格示意圖。

對于某些特殊工程周邊布設的臺站，如高鐵沿線地震預警臺站由于需要依據相應的行政區劃分、臺站工作人員生活成本等問題，所以地震臺站在定位過程中造成臺站共線的現象不可避免，而臺站共線無論在傳統定位中，還是在雙曲線定位中都將造成定位結果不唯一。利用Delaunay三角剖分，可以在一定程度上解決臺站共線造成的定位誤差，同時可以通過對臺站觸發順序和臺站位置，對非地震干擾進行剔除。

對于非震動干擾，其各臺站到時順序上是不相關的，即不符合地震震相的傳播規律，此規律可以作為震動信號的邏輯判據。

Delaunay（以下簡稱D）三角剖分是計算幾何學的重要基礎，應用于許多科學領域中。圖2是D三角剖分示意圖，其定義為連接所有相鄰V圖多邊形的生長中心所形成的三角網。可以看出D三角剖分在平面上反映出了各臺站的相鄰關系，可以作為臺站到時順序的邏輯判別依據。

假定地震P波傳播速度恒定且地球介質均勻，臺網對同一次地震第i個接收到P波的臺站，成為第i臺，記為S（i）。由D三角剖分性質和臺站的幾何分布，可以對觸發的干擾信號進行剔除。具體操作如下，如果對于臺網數據我們得到某臺站S（i）的P波到時，則下一個P波到時臺站S（i+1）一定位于以S（i）臺站為頂點的D三角的另一個頂點。運用以上結論，我們對判斷出P波到時錯誤信號進行排除，以前三個臺站為例，方法如下：第1個臺站觸發后，如果觸發的第2個臺站不在第1個臺站周圍的D三角頂點上，則等待第3個臺觸發;如果第3個臺在第1個臺周圍D三角頂點上則認為第2個臺的第1個觸發錯誤，進而判斷第2個觸發到時;如果第3個臺站在第2個臺站周圍D三角頂點上則認為第1個臺第1個到時錯誤;如果三臺D三角互不相關，則把第3臺當成第1臺并循環向下判斷。如果某臺發生多個不相關觸發，則把此臺直接剔除。

2? 計算實例

采用13次天然地震數據對算法進行驗證，數據來源如表1。

圖3為不同臺站數量的定位結果圖中紅色線為定位平均誤差，由圖可見，隨著臺站數量增加，震中定位平均誤差逐漸減小。

2015年12月10日13時27分20秒在山西省忻州市原平市（北緯38.7度，東經113.0度）發生3.2級左右地震，震源深度6千米。距永興莊監測點29.64km，忻州西監測點38.91km，南山監測點54.88km，陽曲西監測點77.17km，歡咀村監測點87.04km，該次地震發生在鐵路沿線附近，距離最近的監測臺站在30km以內。

采用本文上述定位方法的預警系統成功對該次地震進行了預警，圖4為定位結果示意圖，其結果單臺定位誤差為67.17km，雙臺定位誤差為41.55km，三臺定位誤差為9.62km，四臺定位誤差為4.81km，五臺定位誤差為10.63km，未因誤觸發臺站造成地震定位出現偏差。

3? 結論

本文采用基于網格搜索對地震事件進行定位，隨著臺站數量的增多，地震定位誤差逐漸減小。在進行定位計算中，引入Delaunay三角剖分，利用臺站觸發順序可以有效剔除誤觸發的臺站，避免由于誤觸發臺站引入的定位誤差。

參考文獻：

[1]朱元清，趙仲和.提高地震定位精度新方法的研究[J].地震地磁觀測與研究，1997，18（5）：59-66.

[2]楊智嫻，陳運泰.用雙差地震定位法在我國中西部地區地震精確定位中的應用[J].中國科學（D輯），2004，26（2）：115-120.

[3]劉希強，李霞，等.2012a.基于單臺P波初始記錄的地震震中和震級快速測定方法研究[J].地震研究，35（4）：514-521.

[4]金星，張紅才，李軍，等.地震預警連續定位方法研究[J].地球物理學報，2012，03：925-936.