基于統計指數中權數問題的探討

張毅 王力

摘要：統計指數中的權數，既是同度量因素，起媒介作用，又是權數，起權衡輕重的作用，如何運用權數去分析和解決實際問題，以及特殊權數的運用，對社會經濟現象的分析都將有重要意義。本文重點探討統計指數中的權數問題。

Abstract： The weights in the statistical index are not only the same measure factor with media function， but also the weight， playing a balancing role. How to use the weights to analyze and solve practical problems， and the application of special weights will have important implications to the social economy. This article focuses on the issue of weights in statistical indices.

關鍵詞：指數;權數;特殊權數;交叉權數

Key words： index;weight;special weight;cross weight

中圖分類號：C813? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1006-4311（2018）35-0236-03

0? 引言

權數在統計學原理中，盡管應用廣泛，但研究者甚少，仁者見仁，智者見智，針對不同的內容，有不同的理解，特別是運用權數來分析實際經濟現象，更是薄弱環節。 在統計教學中，權數問題也一直都是困擾學生的一個重點和難點內容，特別是統計指數中，如何運用權數去分析和解決實際問題，更是難點，結合多年教學經驗，談談對指數中權數問題的認識。

1? 權數的基本概念

權數是統計學中應用十分廣泛的一個基本概念，據古籍中注釋，“錘謂之權”，“錘”即我們今天說的秤鉈。俗話說“秤鉈雖小壓千斤”。“秤錘”，即有權衡輕重之義，統計學原理中正是運用了這一詞義，把起權衡輕重作用的數稱為“權數”。最早出現權數是在平均數中，一般的理解是“次數”就是權數，它可以表現為絕對數，也可以表現為相對數，對平均數的大小起權衡輕重的作用;在時間數列中，“間隔時間”就是權數;在統計指數的學習中，同度量因素就是權數，本文重點探討指數法中的權數問題。

2? 統計指數中的權數

在指數的學習中，有一個非常重要的概念，就是同度量因素，同度量因素有兩個作用，一是同度量的作用，把不能直接相加的因素過渡到可以相加，起了媒介作用;二是權數作用，有權衡輕重之意。所以，指數法中的權數就是同度量因素，在分析社會經濟現象中，對其權數有不同的理解，形成了不同的派別。

2.1 綜合指數中的權數

在指數的學習中，綜合指數的編制有兩種形式，即數量指標指數和質量指標指數，為了解決同度量問題，使不同使用價值的現象改變為價值形態，使用了同度量因素，既解決了不同度量的問題，起到了媒介作用，又起到權數作用。

2.1.1 質量指標為權數

以數量指標指數為例。

下面通過一個例子可以看[1]出數量指標綜合指數的編制及權數選擇。

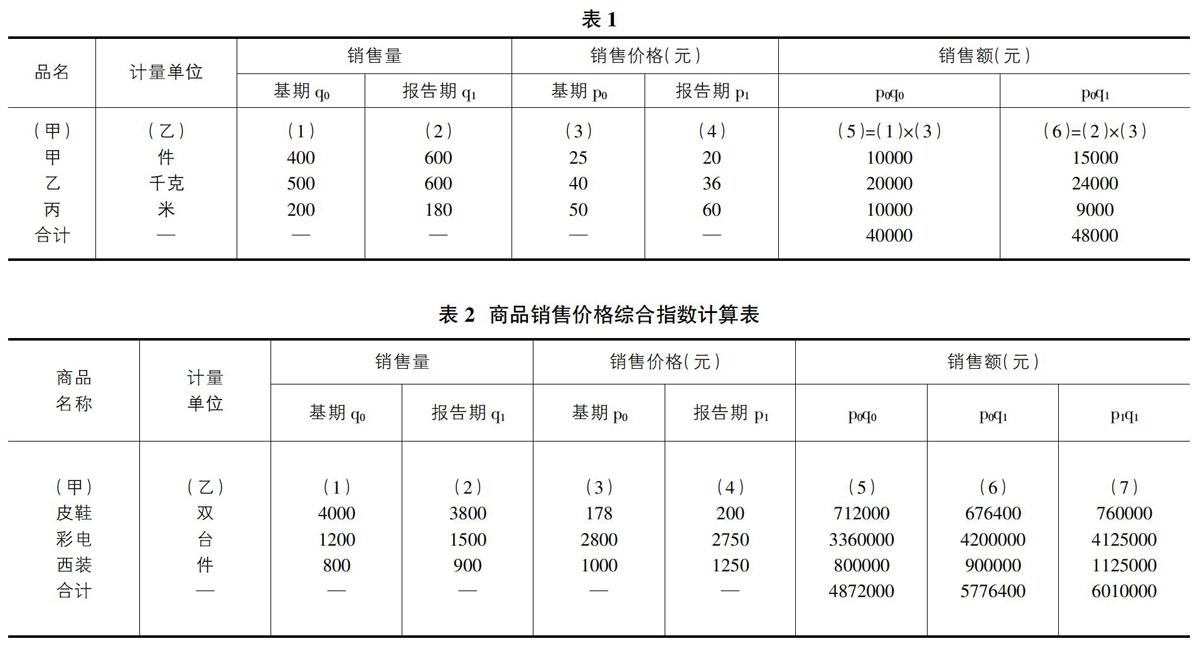
例如，商品銷售量綜合指數計算表，見表1。

以基期價格為同度量因素，即用p0為權數，則商品銷售量綜合指數基本公式

計算結果表明：三種商品銷售量平均增長16.84%，增加銷售額6400元。

拉氏指數和派氏指數都有一定的經濟意義，但是，兩者的區別也很明顯。同度量因素固定在基期，即價格維持在原來的水平，該指數只是單純反映銷售量的變動;如果同度量因素固定在報告期，價格已經發生了變化，在反映銷售量變動的同時，多了一個價格差（P1-P0），那么，究竟該把同度量因素固定在哪個時期呢，具體情況具體分析，多數學者認為，編制數量指標指數，采用拉氏指數較好，更具有現實的經濟意義。

2.1.2 數量指標為權數

以質量指標指標指數為例。（表2）

以報告期銷售量為同度量因素（權數），商品價格綜合指數的基本算式為

計算結果表明，在銷售量不變的情況下，商品價格綜合指數增長4.68%，增加銷售額228000元。

兩個不同時期為權數，計算的結果不同。編制物價指數的目的，不僅要反映物價總變動的方向和程度，還要考察價格變動的實際經濟效果。以報告期銷售量為同度量因素計算的質量指標指數，可以反映當前現實生活中全部商品價格的總變動，以及這種變動對人們生活和國家財政收支的影響，具有現實的經濟意義。

上述分析可以看出：質量指標指數和數量指標指數互為權數，從經濟意義出發，編制質量指標指數，數量指標為權數，并且固定在報告期;編制數量指標指數，質量指標為權數，并且固定在基期。既解決了綜合問題，又保證指數體系的完整。

2.2 特殊權數的應用

2.2.1 固定權數的應用

在編制平均數指數中，采用固定權數編制加權平均數指數在國內外得到廣泛應用。由于缺乏或不需要全面統計資料，無法或不需要直接用綜合指數編制指數時，采用加權平均數指數公式編制指數。其公式（其中）W表示零售額比重權數，由于這種零售額指數，分為小類指數、大類指數和總指數逐級進行編制，因此，也分級確定比重權數，各級權數之和等于100%。這種指數所使用的權數可以用各種有關的抽樣調查資料，用相對數形式固定下來，一定時期內不變（如5年、10年），所以也叫做固定加權算術平均數指數。對個體商品物價指數在物價總指數形成中的重要程度起著權衡輕重的作用，我國的物價指數就是用這種方法計算和編制的，所用的權數是經過調整的基期銷售額。

2.2.2 不變權數與可變權數的應用

在指數數列中，由于各個時期指數采用同度量因素所屬時期是否變動，還產生了可變權數和不變權數問題。各個時期指數用著不同時期的同度量因素，它們是變動的，稱為可變權數;各個時期指數的同度量固定在一個時期水平上，它們是不變的，稱為不變權數。

以數量指標指數數列為例，

環比指數數列：

編制數量指標指數時，要求權數固定在基期，由于環比指數要求依次以前期為基期，權數的時期隨基期的變動而變動，所以叫可變權數，在定基指數數列中，各個時期的權數被固定在基期，沒有變化，所以叫不變權數。

以質量指標指數數列為例，

編制質量指標指數，由于要求權數固定在報告期，所以無論是環比指數數列還是定基指數數列，權數總是隨報告期的變動而變動，其權數都是可變的，所以是可變權數。

在實際工作中，用不變價格為權數編制產量指數，這種不變價格，系根據某一時期的全國平均價格來確定的，一旦確定后，在一段時間內固定不變，是一種特殊應用的“不變權數”，公式為：（pn為不變價格）。

2.2.3 股票價格指數的應用

3? 總結

綜上所述，統計指數中的權數，表現形式很多，無論以什么數量形式出現，它都是一個相對數，準確說是一個結構相對數，其實質都在于它對所計算和分析的指標起著權衡輕重的作用，正確認識和理解了權數的實質，將有助于統計相關理論的學習。

參考文獻：

[1]賈俊平.統計學基礎[M].三版.中國人民大學出版社，2011（2）.

[2]張毅.統計學基礎[M].中國商業出版社，2011（8）.

[3]張舉剛.統計學基礎[M].重慶大學出版社，2004（8）.

[4]邢春玲.統計學原理[M].重慶大學出版社，2008（10）.

[5]向容美.國民經濟統計概論[M].西南財經大學出版社，1996（2）.

[6]何曉群.多元統計分析[M].四版.中國人民大學出版社，2015（4）.

[7]陳仁恩.社會經濟統計學原理[M].中央廣播電視大學， 1996（10）.