慣性本質假設

孫崇江

摘要：本文通過物體轉動所具有的軸向穩定性，并借鑒當年安培提出的“分子電流假設”而成功解釋磁現象的認識，提出慣性本質的自轉說：可將宏觀物體看作由無限個繞軸轉動的微小陀螺構成，每個微小陀螺轉動方向的取向雜亂無章且具有軸向穩定性，取向是沿各個方向均等的。即從宏觀上來看，物體沿任一方向就具有保持軸向穩定的特性，所以宏觀物體沿任一方向都具有慣性的特征。

關鍵詞：慣性;本質;慣性質量

自伽利略發現“慣性原理”到牛頓的“牛頓第一定律”“牛頓第二定律”至今，自然科學尤其是物理學取得了令人滿意的成果，因為物理學的成功，推動了自然科學的進一步發展。但經典物理學在發展的過程中也留下了一些遺憾，直到現在，我們在理解或解釋慣性時，通常是用慣性現象解釋慣性，或用“牛頓第一定律”“牛頓第二定律”相互說明，并強調“慣性是物體所固有的屬性”，至于為什么，就沒有進一步的解釋了。不少物理學書籍還附加一個說法：由于客觀世界找不到不發生相互作用的物體，物體不受其他物體的作用是理想情況，所以“牛頓第一定律”永遠無法用實驗來驗證。就是這一解釋為慣性及慣性定律打上了神秘的烙印，也為物理學后來進一步認識慣性的本質蒙上了一層陰影。到目前為止，各級各類物理學書籍在有關“慣性原理”“牛頓第一定律”及“牛頓第二定律”的討論中都不觸及或回避慣性本質這一問題。

那么，慣性究竟是怎樣產生的？物體為什么具有慣性？我們可以通過以下的討論及演繹推理，逐步加深對慣性本質的認識，也許能給出一個關于慣性本質的基本假設。

首先，我們討論問題的基礎或前提條件是伽利略的“慣性原理”和牛頓的“慣性定律”及慣性的概念。伽利略首先提出“慣性原理”，牛頓在總結力學的基本規律時把它稱為“第一運動定律”或“慣性定律”，具體描述是：任何物體都要保持勻速直線運動或靜止狀態，直到外力迫使它改變運動狀態為止。可見，物體具有保持原來運動狀態的本領或屬性即慣性，這是伽利略及牛頓等物理學前輩為我們總結出的基本物理學規律，當然，我們在生活中也能夠切實地感受到。從前輩對慣性所下的定義可知：

一是慣性具有普遍性，無論是何種材料的物體，無論是固體、液體、氣體，不管其質量的多少，它們在任何時刻、任何位置、任何運動狀態都具有慣性;

二是慣性具有各向同性，無論物體以何種狀態存在、在何位置，無論物體處于何種運動狀態，物體沿各個方向所體現出的慣性特征都是相同的。

由慣性的定義及其普遍性、各向同性的特征，我們應該可以去探索慣性產生的原因，認識慣性的本質。所以，本文認為，慣性是由物質的某種特殊的運動形式產生的。

根據以上理解我們似乎能找到物體具有慣性的蜘絲馬跡，或許能為回答慣性的本源問題提出可供參考的創新思路。

為了探索慣性的本源問題，我們先從生活中的實例來歸納總結，然后再進行推理及演繹。

現象一：轉陀螺是許多孩子喜歡的游戲。無論是大陀螺還是小陀螺，只要制作勻稱（即沿自轉軸陀螺的質量分布均勻），在游戲中當陀螺的轉動達到一定的速度時，它沿轉軸就具有穩定性。陀螺質量越大轉速越大，在游戲過程中的穩定性就越明顯、持續時間也越久，亦即陀螺沿轉軸穩定性就越強。

現象二：取一個圖釘，以其針尖端為支點使其高速轉動，我們同樣可以觀察到圖釘轉動時沿轉軸方向具有穩定性。

同理，我們可以制作出更大或更小的陀螺來再現其沿轉軸方向的穩定性這一特征。

將上述有關陀螺轉動時沿轉軸方向具有穩定性的試驗由大到小、由小到微小及進一步延伸到微觀狀態下去認識陀螺現象，我們似乎可以推測出：只要能制作出足夠小（或在自然界中能找得到）的陀螺，當它沿轉軸轉動時一定具有沿軸向穩定性的特征。

這樣，我們可以歸納出以下結論：一切轉動的物體沿軸都具有穩定性的性質，并且沿轉軸轉動時的軸向穩定性與轉動慣量及轉速成正比，而這兩個物理量正好體現在物體的轉動動能中。物體轉動時轉動慣量越大、轉速越大，它的轉動動能就越大，所以轉動動能E轉動= ■ Iω2是物體沿轉軸轉動時的軸向穩定性的一個重要指標。

事實上，我們知道運動是物質的基本屬性，而轉動又是物質運動的重要形式。我們可以想象，由宏觀上比較大的陀螺到比較小的陀螺、再到更微小至深入到微觀的粒子來看，只要發生轉動，無論它們的幾何限度大小的差別怎樣，它們都具有沿轉軸方向穩定取向的特征。因此我們仿照當年安培提出的“分子電流假設”那樣，提出如下假設：在研究物體的慣性時，我們完全可以將宏觀物體看作由無限個轉動的微小陀螺構成，每一個微小陀螺轉動時，其沿轉軸轉動時都具有軸向穩定性，而這些微小粒子的轉軸方向取向是雜亂無章的，且其轉軸本身也隨空間和時間不斷變化，從統計學上來說，這些微小陀螺的轉動方向的取向是沿各個方向均等的。即從宏觀上來看，物體沿任一方向就具有保持軸向穩定的特性，亦即宏觀物體沿任一方向都具有慣性的特征。這就是物體為什么具有慣性的原因，我們把這一假說稱為“慣性本質的自轉說”或“慣性本質的陀螺說”。

本假說的要點是首次把慣性產生的原因與物體轉動聯系起來。為了方便研究物體的慣性，我們可以把組成物體的微小陀螺鎖定在某一微觀粒子的尺度范圍上，也就是說把這一微觀粒子看作是物體慣性的基本單元，就定義為“慣性元”或“陀螺子”。

無論這個假說正確與否，通過理論研究和實驗驗證的路徑去肯定或否定這個假說都將深化對慣性本質的認識。

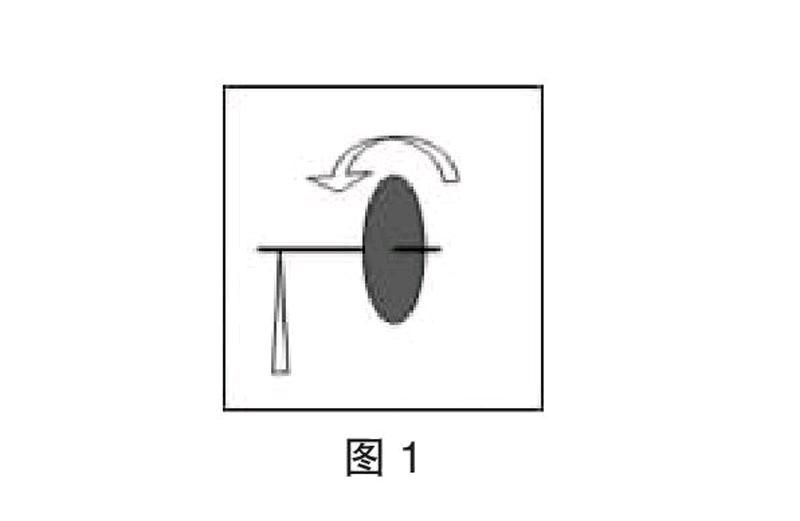
根據以上假設，我們從宏觀上來討論物體的慣性。假設質量為m的物體以ω0角速度轉動時剛好具有軸向穩定性，如圖1所示，此時對應的角速度ω0稱為臨界慣性角速度。當物體以某角速度ω轉動時：

若ω﹤ω0，則轉動物體不具備軸向穩定性;

若ω=ω0，則轉動物體剛好具有軸向穩定性;

若ω﹥ω0，則轉動物體具有較強的軸向穩定性;

若ω﹥﹥ω0，則轉動物體具有很強的軸向穩定性。

注意：在研究物體的慣性時，忽略轉動物體的進動。

再來看慣性系數和慣性質量。

1.慣性系數

如圖1，在重力場中，有一質量分布均勻，半徑為R、質量為m的圓盤繞過盤心垂直于盤面的軸轉動，設支點到盤心的距離為R（忽略圓盤的進動），維持圓盤保持平衡的最小角速度是ω0。

分析：根據以上對慣性本質的假設，物體在具有最小轉動角速度ω0情況下克服自身重力矩作用而保持平衡，這是物體保持原來運動狀態的基本條件。

注意：轉動物體的轉軸與豎直方向可以是任意夾角α，則物體對支點的重力矩為M1=mgR·Sinα，但考慮到（ω﹤ω0時）當α>90o時，轉動物體將失去軸向穩定性。為了簡化問題，我們取α=90o，如圖2：

本文是將具有轉動的某一層次的微觀粒子選作為“慣性元”基礎而提出的“慣性本質假設”，這實際上是認識慣性本質的其中一步。也許可以從其他角度去進一步研究、認識慣性的本質。※endprint