面向成本的雙邊裝配線平衡和員工分配

邱玉蓮，彭嬋娟

（武漢科技大學 管理學院，湖北 武漢 430081）

1 引言

裝配線廣泛存在于制造業中，裝配線的平衡與否直接關系到裝配線的效率和企業的成本。作為一種特殊的裝配線形式，雙邊裝配線以其裝配線長度短、搬運成本低等[1]優勢廣泛應用于汽車、卡車等產品的總裝線上。

雙邊裝配線平衡問題根據目標可主要分為兩類：第一類問題[2-3]，給定生產節拍，在滿足生產線約束條件的前提下最小化工位數量；第二類問題[4-6]，給定工位數量，在滿足生產線約束條件的前提下最小化生產節拍。目前國內外主要研究集中于第一類雙邊裝配線平衡問題，已有多種算法[2-3]應用于求解該NP難題。相較于第二類雙邊裝配線平衡問題，目前僅有遺傳算法[4]、蟻群算法[5]、粒子群算法[6]等用于求解該問題。由上可知，科研對第二類雙邊裝配線的平衡研究很少，但是第二類雙邊裝配線問題在實際中對于消除瓶頸工位、提高負載均衡有著廣泛的應用前景。

以上研究均假設所有員工對相同操作的完成時間相同，但是在實際生產中由于員工技能的差異對相同的操作的完成時間可能不同[7]，例如殘疾人完成需要站立的操作耗時巨大，因此在實際生產中需要考慮員工的分配問題。同時在企業的裝配成本中，員工工資成本是其支出的主要部分[8]，所以企業越來越關注減少工資支出。由于工資成本的最優化與裝配線的平衡可能出現沖突，所以需要采用多目標優化。

針對第II類多目標雙邊裝配線平衡和員工分配問題，提出一種多目標重啟模擬退火算法實現平衡和成本的同步優化。設計了新的編碼和解碼方式以實現工位負載均衡和減少序列相關空閑時間，采用了重啟機制以獲得分布性更好的前沿解。同時將重啟模擬退火算法與快速非支配排序遺傳算法進行對比，證明了算法的高效性。

2 雙邊裝配線平衡和員工分配

2.1 問題介紹

在雙邊裝配線上，如圖1所示。左右兩個工位合稱為成對工位，每個工位上均分配有相應操作。第II類雙邊裝配線員工分配和平衡問題可分為兩個子問題，即員工分配和裝配線平衡問題。在員工分配中，每個工位分配一個員工，其對同一操作的完成時間可能區別于其他員工。在裝配線平衡中，每個操作在滿足有限關系約束、方向約束的情況下被分配到對應的工位。

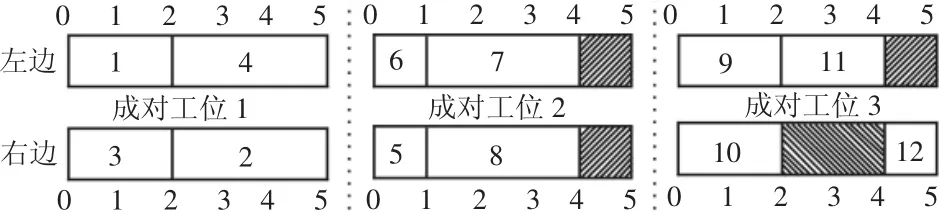
圖1 雙邊裝配線工位布置Fig.1 Task Assignment of Two-Sided Assembly Line

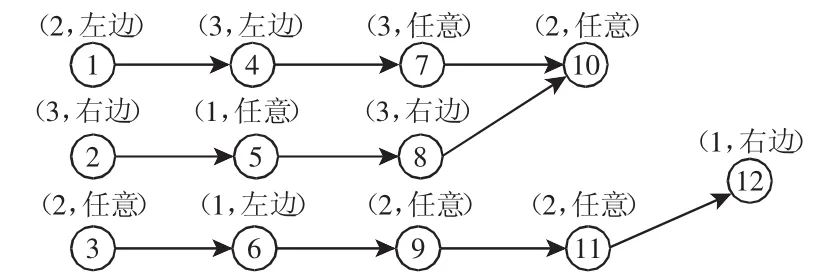
圖2 操作數為12的優先關系圖Fig.2 Precedence Diagram for 12-Task Problem

對應圖1分配方案的優先關系圖，如圖2所示。圖2中，共有3類不同操作，分別為：操作方向為左邊的操作（L），操作方向為右邊的操作（R）和操作方向為任意方向的操作（E）。圖中，圓圈內的數字代表操作，圓圈上的標簽代表操作的作業時間和操作的方向。圓圈間的箭頭代表操作間的優先關系，以操作1和4間的箭頭為例，其代表操作1是操作4的前序。

2.2 問題模型

為同步優化工資成本和負載平衡，分別設計了如下兩個目標，如式（1）、式（2）所示。依次對應工資成本和負載均衡。為簡化起見，以下主要說明兩個目標函數，其它優先關系、員工分配等約束請參考相關文獻[3，7]。

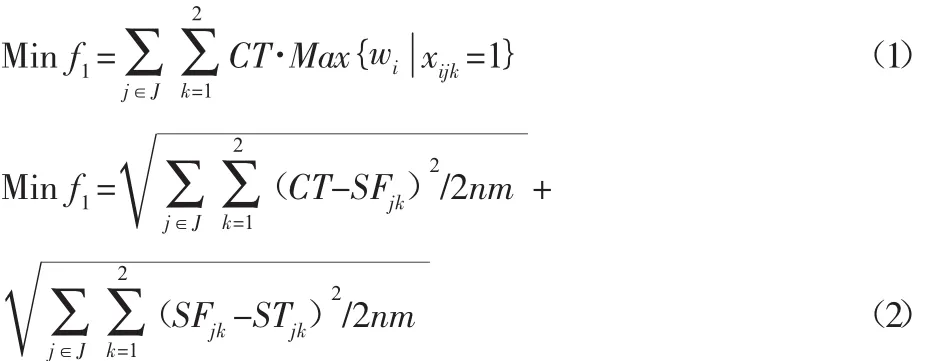
式中：i—操作；j—成對工位；k—成對工位的左右兩邊；J—成對工位集合；wi—單位時間內操作i的工資；CT—節拍；SFjk—工位（j，k）最后一個操作的完成時間；STjk—工位（j，k）分別的操作的加工時間總和；xijk判斷操作i是否分配到工位（j，k），如果分配到工位（j，k）取值1，否則取值為0。

式（1）中工資成本設置文獻[8]，其中單位時間內每個操作的工資水平由操作的難度決定，整個工位的單位工資水平由分配到該工位的最難的操作對應的單位工資水平決定。式（2）的前半部分最小化工位最后完成時間的偏差，后半部分最小化工位實際分配負載的偏差。

3 重啟模擬退火算法

模擬退火算法廣泛應用于各類優化問題，例如裝配線平衡問題[2]。模擬退火算法是基于鄰域的局部搜索算法，由于所研究的問題為多目標問題，設計了新的接受準則和重啟機制。

3.1 編碼及解碼

由于考慮的問題涉及到裝配線平衡和員工分配兩個問題，所以采用了3個數組進行編碼，分別為員工分配數組，操作分配數組和操作排序數組.以下以一個案例說明編碼和解碼情況，如圖3所示。其中，員工分配數組中第一個位置的3表示，第一個成對工位的左邊分配的員工編號為3.操作分配決定操作分配的成對工位，操作排序數組決定操作分配的優先級。為獲得每個工位的詳細分配的方案，采用文獻[6]中解碼方式獲得滿足優先關系約束和方向約束的分配方案。需要指明，以上解碼可作為文獻[4]中的解碼的一種改進方式，其通過工位選擇策略實現成對工位內部的負載均衡，通過操作選擇策略有效減少工位上的空閑時間。

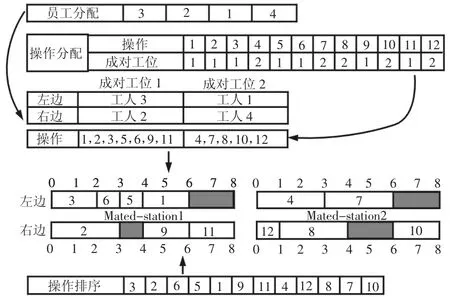
圖3 編碼及解碼Fig.3 Encoding and Decoding Procedure

3.2 鄰域結構設計

由于解碼中涉及了3個數組，所以設計了3種不同的領域結構，介紹如下：（1）針對員工分配的領域結構：采用交換操作。（2）針對操作分配的鄰域結構：采用隨機選擇交換操作和變異操作兩個方式中的一種。變異操作隨機選擇一個操作，將其對應的成對工位變成其他成對工位。（3）針對操作排序的鄰域結構：采用插入操作。在鄰域結構的選擇中，對應每個數組，隨機產生一個0到1之間的小數，如果小于1/3，則對該數據進行變動。以上鄰域選擇方式允許變動多個數組，有效增大搜索空間。

3.3 帕累托解集更新及接受準則

當使用鄰域結構產生一個新解后，如果該解沒被其他任何解支配，則該解被添加到帕累托前沿解集，同時移除前沿解集中被支配的解。更新完帕累托前沿解集后，新產生的解替換原來的解S，即S←S′。當新解被前沿中的某個解支配，采用多項概率密度函數[9]從2個優化目標中選取一個以判斷是否接受該解。在目標概率密度函數中，每個目標被選擇的概率設定為0.5.假設選擇其中一個目標f（*），則目標值的變化為Δ，Δ=f（S′）-f（S）。如果Δ≤0，則新解被接受并替代當前解。否則，按照exp-Δ/（T×f（S））的概率接受該新解，式中：T—溫度參數。

3.4 重啟機制

為增強算法跳出局部最優的能力，設計了一種重啟機制以獲取更多的前沿解，如圖4所示。如果連續dn次迭代均不能發現新的前沿解，則從當前前沿解集中選擇一個解作為代替當前解。改進聚集距離[10]做了如下改進：

（1）極值解的距離設定為1，而非原來的無窮大。

（2）將選擇的次數融入到聚集距離中，且前沿解的聚集距離隨著被選擇次數的增加而逐漸減少。

圖4 重啟機制流程圖Fig.4 The Procedure of Restart Mechanism

3.5 算法流程

在重啟模擬退火算法中，連續執行NS次后鄰域搜索后，對溫度系數T按照T=αT進行更新，式中：α—冷卻系數。詳細算法流程，如圖5所示。

圖5 重啟模擬退火算法流程圖Fig.5 The Procedure of Restarted Simulated Annealing

4 實驗結果與分析

為驗證重啟模擬退火算法的性能，生成了總共7組案例（P9，P12，P16，P24，P65，P148以及P205），并將重啟模擬退火算法與快速非支配排序遺傳算法進行對比[10]。每個員工對操作i的加工時間為［ti×0.8，ti×1.2］之間的隨機數，ti為文獻[4]中操作 i的加工時間。為比較不同算法的性能，采取了3個評價指標，分別為：非支配率、收斂性和分布性，其詳細計算參考文獻[3]。一般來說，非支配率的值越大，則該算法獲得前沿解越好。收斂性越小，則算法收斂性越好。分布性越小，則算法獲得的前沿解的分布性更好。

4.1 算法參數校驗

所提出的算法采用多因素方差分析（ANOVA）進行參數校驗。初始溫度T0設置兩個水平，即0.5和1；冷卻系數設置3個水平，即0.9，0.95和0.98；每個溫度下的迭代次數NS設置3個水平，即500，1000和2000；重啟機制的促發次數dn設置為3個水平，即100，200和300.方差分析的結果，如表1所示。由可知α，NS和dn對應的P值均小于0.01，即存在顯著性差異。按照P值遞增的順序依次選擇每個參數的最優水平，滿足95%最小顯著差數間隔的置信水平的冷卻系數各個取值，如圖6所示。

表1 關于收斂性的多因素方差分析表Tab.1 VNOVA Results for Convergence

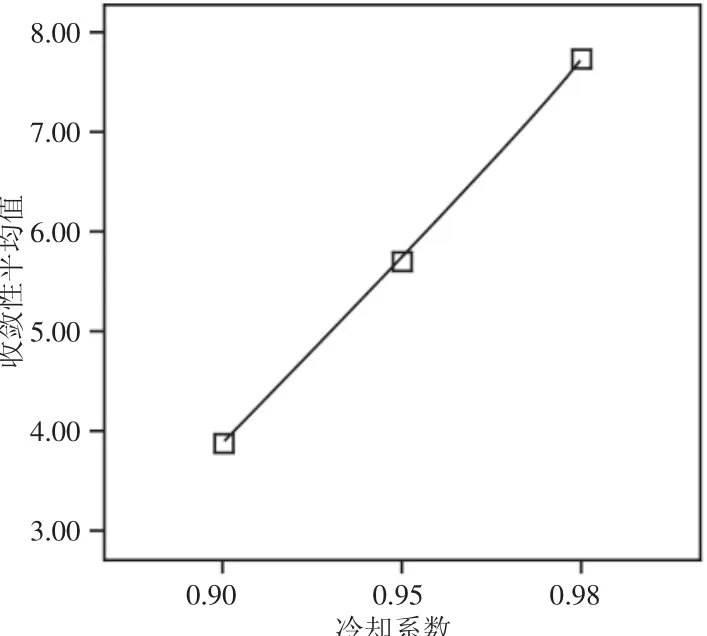
圖6 冷卻系數平均值Fig.6 Mean Plot for Cooling Rate

4.2 算法性能對比

為驗證重啟模擬退火算法的性能，重啟模擬退火算法和快速非支配排序遺傳算法分別對7組案例進行10次求解，算法的終止條件統一設定為運行時間t=nt×nt×10ms。算法的平均結果，如表2所示。由表2可知，針對非支配率，重啟模擬退火算法在總共39個案例上優于快速非支配排序遺傳算法。針對收斂性，重啟模擬退火算法有36個案例都優于快速非支配排序遺傳算法；針對分布性，重啟模擬退火算法有34個案例優于快速非支配排序遺傳算法。針對所有的大規模案例，P65，P148和P205，重啟模擬退火算法在所有案例上均優于快速非支配排序遺傳算法。

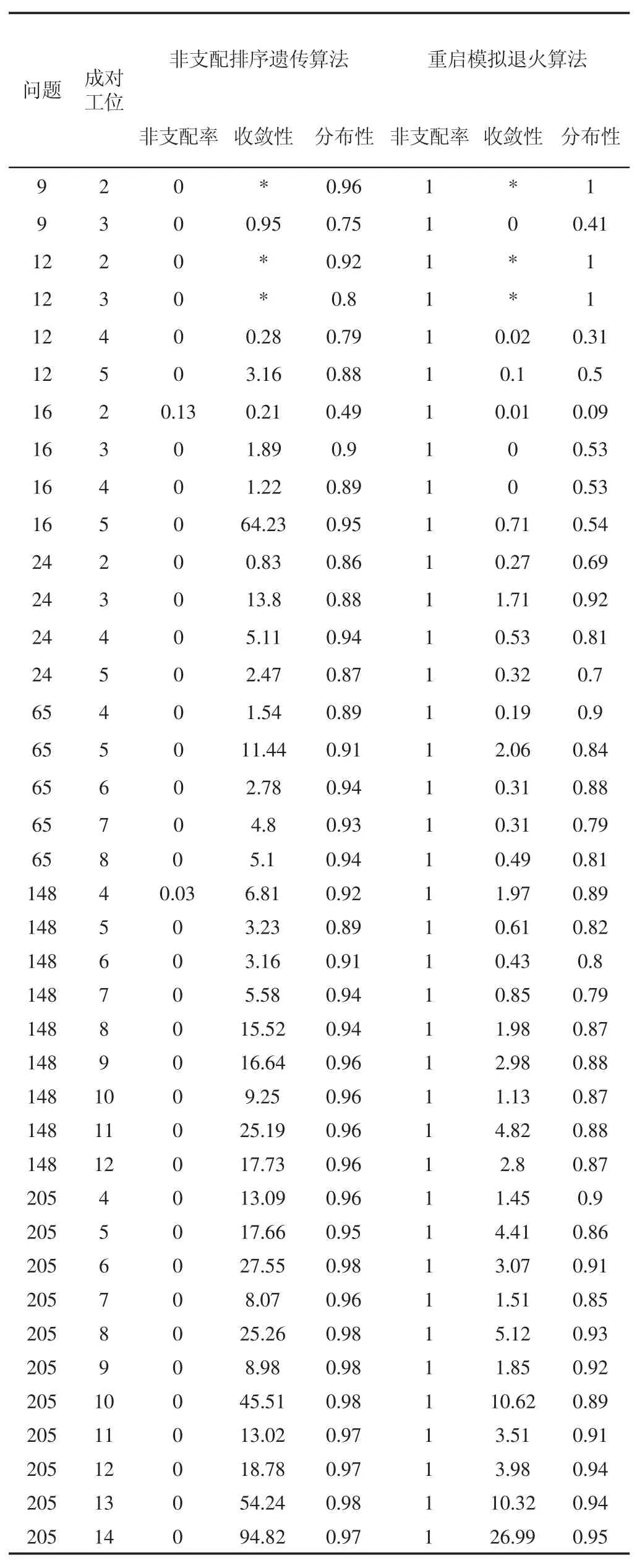
表2 算法的平均結果對比Tab.2 Comparison Results for Average Results

5 結語

針對雙邊裝配線的員工分配和平衡問題，設計了最小化成本和最大化負載均衡兩個目標，建立相關的多目標的優化模型。為求解以上NP難題，提出了一種重啟模擬退火算法。在算法實踐中，針對員工分配和平衡問題，分別設計了有效的鄰域結構。為避免陷入局部最優，基于改進聚集距離提出了重啟機制，以獲得分布性更廣的前沿解。為驗證重啟模擬退火算法的性能，生成了7組案例，并與快速非支配排序遺傳算法的性能進行對比。試驗結果表明，所提出的算法在收斂性和分布性上均優于快速非支配排序遺傳算法。下一步研究可將重啟模擬退火算法應用于其他多目標優化問題。

［1］J.J.Bartholdi.Balancing two-sided assembly lines：A case study［J］.The International Journal of Production Research，1993，31（10）：2447-2461.

［2］D.Khorasanian，S.R.Hejazi，G.Moslehi.Two-sided assembly line balancing considering the relationships between tasks［J］.Computers&Industrial Engineering，2013，66（4）：1096-1105.

［3］李大雙，張超勇，邵新宇.基于多目標殖民競爭算法的隨機型雙邊裝配線［J］.計算機集成制造系統，2014，20（11）：2774-2787.（Li Da-shuang，Zhang Chao-yong，Shao Xin-yu.Balancing stochastic twosided assembly line with multi-objective colonial competitive algorithm［J］.Computer Integrated Manufacturing Systems，2014，20（11）：2774-2787.）

［4］Y.K.KIM，W.S.SONG，J.H.KIM.A mathematical model and a genetic algorithm for two-sided assembly line balancing［J］.Computers&Operations Research，2009，36（3）：853-865.

［5］鄭巧仙，李明，李元香.求解雙邊裝配線平衡問題的改進蟻群算法［J］.電子學報，2014，42（5）：841-845.（Zheng Qiao-xian，Li Ming，Li Yuan-xiang.An improved ant colony optimization for two-sided assembly line balancing problem［J］.Acta Electronica Sinica，2014，42（5）：841-845.）

［6］李梓響，唐秋華，林斌.第二類雙邊裝配線平衡的混合粒子群算法［J］.機械設計與制造，2015（1）：113-116.（Li Zi-xiang，Tang Qiu-hua，Lin Bin.A hybrid particle swarm optimization for two-sided assembly line balancing problem of type II［J］.Machinery Design&Manufacture，2015（1）：113-116.）

［7］P.Th.Zacharia，Andreas C.Nearchou.A population-based algorithm for the bi-objective assembly line worker assignment and balancing problem［J］.Engineering Applications of Artificial Intelligence，2016（49）：1-9.

［8］A.Roshani，P.Fattahi，A.Roshani，M.Salehi，A.Roshani.cost-oriented twosided assembly line balancing problem：a simulated annealing approach［J］.International Journal of Computer Integrated Manufacturing，2012，25（8）：689-715.

［9］S.Kulturel-Konak，A.E.Smith，B.A.Norman.Multi-objective tabu search using a multinomial probability mass function［J］.European Journal of Operational Research，2006，169（3）：918-931.

［10］K.Deb，A.Pratap，S.Agarwal，T.Meyarivan.A fast and elitist multiobjective genetic algorithm：NSGA-II［J］.IEEE Transactions Evolutionary Computation，2002，6（2）：182-197.