基于后驗(yàn)量測(cè)修正的卡爾曼濾波算法

，，

(解放軍電子工程學(xué)院，安徽 合肥 230037)

0 引言

卡爾曼濾波是一種遞推的線性最小均方誤差估計(jì)，廣泛應(yīng)用于自動(dòng)控制、目標(biāo)跟蹤、組合導(dǎo)航等領(lǐng)域[1-5]。標(biāo)準(zhǔn)的卡爾曼濾波器是以精確的數(shù)學(xué)模型和已知的噪聲統(tǒng)計(jì)特性為前提，進(jìn)行遞推濾波，取得最優(yōu)估計(jì)的。但在實(shí)際工程中，系統(tǒng)的模型參數(shù)以及噪聲統(tǒng)計(jì)特性通常難以獲取，導(dǎo)致卡爾曼濾波精度下降，甚至濾波發(fā)散[6]。此外，卡爾曼濾波器在狀態(tài)收斂時(shí)，其誤差協(xié)方差矩陣和增益矩陣趨于極小值，狀態(tài)改變時(shí)，不能及時(shí)調(diào)整增益矩陣及協(xié)方差矩陣，導(dǎo)致濾波器喪失對(duì)突變狀態(tài)的跟蹤能力。

針對(duì)標(biāo)準(zhǔn)卡爾曼濾波器的不足，目前的改進(jìn)方式主要分為兩類：一是建立合適的估計(jì)準(zhǔn)則，利用新增的量測(cè)信息，對(duì)模型的參數(shù)和噪聲統(tǒng)計(jì)特性進(jìn)行在線調(diào)整，實(shí)現(xiàn)自適應(yīng)濾波[7-8]；二是把系統(tǒng)模型及噪聲統(tǒng)計(jì)特性不準(zhǔn)確所帶來的誤差等效為濾波誤差，采用漸消因子抑制濾波器的記憶長(zhǎng)度，充分利用當(dāng)前的量測(cè)數(shù)據(jù)，減小陳舊量測(cè)的影響，實(shí)現(xiàn)漸消濾波[9]。第二類算法僅需要額外增加一個(gè)漸消因子的計(jì)算，通過該漸消因子對(duì)預(yù)測(cè)協(xié)方差進(jìn)行修正，間接調(diào)整增益，從而增強(qiáng)濾波器的調(diào)節(jié)能力。由于實(shí)現(xiàn)簡(jiǎn)單，實(shí)用性強(qiáng)，得到了廣泛應(yīng)用[10-13]。然而，文獻(xiàn)[14]進(jìn)一步指出，該類算法雖然能較好地解決濾波發(fā)散、增強(qiáng)濾波器對(duì)突變狀態(tài)的跟蹤能力，但是仍然存在以下缺陷：1)在模型參數(shù)及噪聲統(tǒng)計(jì)特性已知的情況下，漸消因子的引入反而會(huì)降低濾波的精度；2)通過漸消因子來增強(qiáng)對(duì)當(dāng)前量測(cè)的信任存在修正延后。該文獻(xiàn)將引起卡爾曼濾波器發(fā)散的原因歸結(jié)為對(duì)狀態(tài)預(yù)測(cè)值的不準(zhǔn)確，提出對(duì)狀態(tài)預(yù)測(cè)值進(jìn)行實(shí)時(shí)修正，解決了修正延后的問題。但是該算法需要根據(jù)經(jīng)驗(yàn)預(yù)先設(shè)定一系列的修正參數(shù)，存在參數(shù)選取困難。針對(duì)上述算法的不足，本文提出了基于后驗(yàn)量測(cè)修正的卡爾曼濾波算法。

1 目標(biāo)跟蹤建模與修正思路

假設(shè)目標(biāo)的運(yùn)動(dòng)狀態(tài)和量測(cè)模型均為線性模型，則離散狀態(tài)方程和量測(cè)方程可以表示為：

xk=Fk-1xk-1+Γk-1vk-1

(1)

zk=Hkxk+wk

(2)

式中，F(xiàn)k為狀態(tài)轉(zhuǎn)移矩陣；Hk為量測(cè)轉(zhuǎn)移矩陣；Γk為過程噪聲分布矩陣；vk、wk為零均值的白色過程噪聲和量測(cè)噪聲序列，其協(xié)方差分別為Qk、Rk，且任意時(shí)刻vk與wk不相關(guān)。由于Fk、Hk、Γk通常為時(shí)不變矩陣，故下文統(tǒng)一省略時(shí)間下標(biāo)k，簡(jiǎn)記為F、H、Γ。

離散時(shí)間卡爾曼濾波器的狀態(tài)預(yù)測(cè)和狀態(tài)更新方程為：

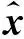
(3)

(4)

式中，Kk+1為濾波增益矩陣。

2 基于后驗(yàn)量測(cè)修正的卡爾曼濾波算法(PMKF)

2.1 后驗(yàn)量測(cè)卡爾曼濾波(PKF)

為了對(duì)卡爾曼濾波器進(jìn)行修正，本節(jié)提出一種利用后驗(yàn)量測(cè)進(jìn)行濾波更新的卡爾曼濾波新算法(PKF)，即利用后驗(yàn)量測(cè)zk+1建立對(duì)k時(shí)刻的狀態(tài)估計(jì)。

將量測(cè)方程向前反推一步，把式(1)代入式(2)中有：

zk=Hxk+wk=
H(Fxk-1+Γvk-1)+wk=
HFxk-1+HΓvk-1+wk

(5)

為方便描述，定義

(6)

則新的量測(cè)方程可以改寫為：

(7)

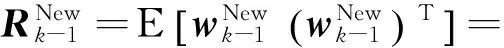
(8)

由于卡爾曼濾波器是線性濾波器，因此，基于后驗(yàn)量測(cè)改寫后的算法要在卡爾曼濾波器的框架下進(jìn)行迭代更新，其狀態(tài)方程與量測(cè)方程也必須是線性的。下面，對(duì)這一點(diǎn)進(jìn)行說明。

因?yàn)镻KF對(duì)狀態(tài)方程沒有改動(dòng)，因此只需要證明其量測(cè)方程是線性的即可。

zk+1=Hxk+1+wk+1=
H(Fxk+Γvk)+wk+1=
HFxk+HΓvk+wk+1=
(HF)xk+(HΓvk+wk+1)

(9)

由式(9)可知，由于H、F為時(shí)不變的常量矩陣，所以，k時(shí)刻的狀態(tài)xk與后驗(yàn)量測(cè)zk+1滿足線性關(guān)系(HF)，即量測(cè)方程是線性的。此外，后面的噪聲項(xiàng)等于兩個(gè)獨(dú)立的高斯分布經(jīng)線性變換后求和，仍然為高斯分布。因此，PKF與KF一樣，是線性、高斯的，可以在標(biāo)準(zhǔn)的卡爾曼濾波框架下進(jìn)行濾波更新。

PKF的一個(gè)濾波流程為：

步驟1 時(shí)間更新

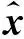
(10)

Pk|k-1=FPk-1|k-1FT+ΓQk-1ΓT

(11)

步驟2 量測(cè)更新

(12)

Pk|k=Pk|k-1-Pk|k-1(HNew)T(Sk)-1HNewPk|k-1=

Pk|k-1-Pk|k-1FTHT(Sk)-1HFPk|k-1

(13)

式中：

HFPk|k-1FTHT+HΓQk-1ΓTHT+Rk

(14)

Kk= [Pk|k-1(HNew)T+ΓQk-1ΓTHT](Sk)-1=

(Pk|k-1FTHT+ΓQk-1ΓTHT)(Sk)-1

(15)

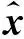
2.2 判決準(zhǔn)則

工程應(yīng)用中，一般根據(jù)新息大小計(jì)算一個(gè)檢驗(yàn)量，用于判斷濾波是否異常。如果正常，則按一般的濾波步驟進(jìn)行估計(jì)，否則，進(jìn)行適當(dāng)?shù)男拚Ｅ袛酁V波異常的判據(jù)為[15]：

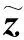
(17)

Pk|k-1=FPk-1|k-1FT+Qk-1

(18)

將式(17)，(18)代入式(16)中，取最嚴(yán)格的收斂判據(jù)ε=1，可得

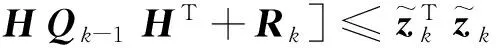
(19)

分析式(19)的左邊不難發(fā)現(xiàn)，過程噪聲協(xié)方差Q和量測(cè)噪聲協(xié)方差R分別由目標(biāo)和觀測(cè)系統(tǒng)決定，通常不隨目標(biāo)的運(yùn)動(dòng)發(fā)生顯著變化。但是第一項(xiàng)包含反映估計(jì)誤差的協(xié)方差矩陣P，在目標(biāo)狀態(tài)改變時(shí)，隨著跟蹤精度下降，P會(huì)增大。在目標(biāo)狀態(tài)持續(xù)性變化，并保持變化強(qiáng)度不變的情況下，P增大，會(huì)抬高檢測(cè)的門限，使得對(duì)突變狀態(tài)的檢測(cè)能力被削弱。故本文提出，去掉不等式左邊第一項(xiàng)，判決條件變?yōu)椋?/p>

(20)

上式左邊的物理意義是明確的，為狀態(tài)噪聲和量測(cè)噪聲的協(xié)方差之和。也就是說，在目標(biāo)狀態(tài)不發(fā)生改變的情況下，量測(cè)值偏離真實(shí)值的最大誤差上限為狀態(tài)噪聲與過程噪聲之和，這正好與實(shí)際情況相符。如果量測(cè)值偏離的程度超過了最大誤差上限，只能是目標(biāo)的狀態(tài)已經(jīng)發(fā)生改變。因此，利用式(20)作為目標(biāo)狀態(tài)改變的判據(jù)更加合理。進(jìn)一步可以發(fā)現(xiàn)，當(dāng)目標(biāo)狀態(tài)持續(xù)性變化時(shí)，由于不等式左邊不發(fā)生變化，因此對(duì)狀態(tài)突變的檢測(cè)能力沒有下降。

2.3 修正的卡爾曼濾波算法

根據(jù)2.1節(jié)、2.2節(jié)提出的PKF算法和判決準(zhǔn)則，基于后驗(yàn)量測(cè)修正的卡爾曼濾波算法(PMKF)的修正流程圖如圖1所示，具體步驟如下。

步驟1：利用zk對(duì)k-1時(shí)刻的狀態(tài)和協(xié)方差進(jìn)行標(biāo)準(zhǔn)的卡爾曼濾波更新；

步驟2：進(jìn)行一步預(yù)測(cè)，并求取k+1時(shí)刻的新息向量；

步驟4：若新息超過判決門限，利用后驗(yàn)量測(cè)卡爾曼(PKF)進(jìn)行濾波更新。否則，直接輸出濾波結(jié)果；

步驟5：重復(fù)步驟1～4。

該修正方法的優(yōu)勢(shì)有兩點(diǎn)：1)當(dāng)檢測(cè)到k+1時(shí)刻的目標(biāo)狀態(tài)發(fā)生改變時(shí)，對(duì)k時(shí)刻的狀態(tài)進(jìn)行調(diào)整，通過時(shí)不變矩陣F的傳遞，達(dá)到修正預(yù)測(cè)值xk+1|k的目的，解決了修正延后的問題。2)對(duì)k時(shí)刻的估計(jì)值進(jìn)行修正時(shí)利用了量測(cè)zk+1，而修正之后進(jìn)行正常卡爾曼濾波時(shí)，再一次用到量測(cè)zk+1，即充分利用了新近量測(cè)的信息，起到了類似于漸消因子的作用。

3 仿真校驗(yàn)

本文采用勻加速模型，傳感器僅提供位置信息。采用均方根誤差評(píng)價(jià)算法的性能，設(shè)置了如下四種仿真場(chǎng)景，各種仿真場(chǎng)景下，Monte-Carlo次數(shù)1 000次。

表1 場(chǎng)景2目標(biāo)加速度Tab.1 Target acceleration in scene two

表2 場(chǎng)景3目標(biāo)轉(zhuǎn)彎角速度Tab.2 Target turning angle acceleration in scene three

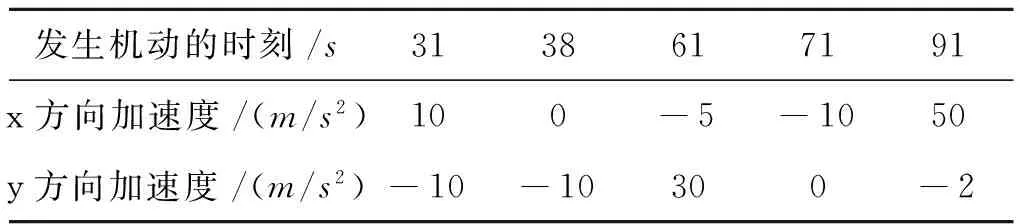
表3 場(chǎng)景4目標(biāo)加速度Tab.3 Target acceleration in scene four

3.1 仿真實(shí)驗(yàn)一

從圖中可以看出，文獻(xiàn)[14]和本文算法對(duì)位置、速度的跟蹤精度均有較大的提高，但是本文算法更為優(yōu)越，尤其是對(duì)位置均方根誤差的改善尤為明顯。然而兩種算法對(duì)加速度的改善都不大，其原因在于傳感器只提供了位置信息，通過位置信息的變化修正速度，再修正加速度，其修正作用逐漸減弱。此外，本文算法在初始狀態(tài)的收斂速度比標(biāo)準(zhǔn)的KF以及文獻(xiàn)[14]略快。

3.2 仿真實(shí)驗(yàn)二

利用場(chǎng)景2測(cè)試本文算法對(duì)加速突變目標(biāo)的跟蹤能力。過程噪聲協(xié)方差Q=diag[1，1，1]，量測(cè)噪聲協(xié)方差R=100，文獻(xiàn)[14]的修正參數(shù)同實(shí)驗(yàn)一。文獻(xiàn)[9]是典型的漸消濾波方法，通過引入漸消因子λ對(duì)預(yù)測(cè)協(xié)方差進(jìn)行修正，進(jìn)而調(diào)節(jié)增益矩陣，達(dá)到增強(qiáng)濾波器對(duì)突變狀態(tài)的跟蹤能力，將其放在相同的場(chǎng)景下進(jìn)行比較。由于對(duì)加速度的改善不明顯，僅給出了標(biāo)準(zhǔn)KF、文獻(xiàn)[14]、文獻(xiàn)[9]以及本文提出的PMKF四種算法的位置及速度估計(jì)誤差曲線，如圖5—圖6。

分析圖5、圖6易知，無論是平穩(wěn)狀態(tài)，還是突變狀態(tài)，本文算法的均方根誤差曲線都保持在較低的水平。因此，PMKF對(duì)狀態(tài)突變具有較好的適應(yīng)能力，相比文獻(xiàn)[14]，調(diào)節(jié)能力更強(qiáng)。文獻(xiàn)[9]由于引入了漸消因子，在平穩(wěn)狀態(tài)時(shí)的跟蹤精度略低于標(biāo)準(zhǔn)的KF，但是在目標(biāo)狀態(tài)改變時(shí)，跟蹤精度較KF有明顯改善，尤其是變化強(qiáng)度比較大時(shí)(體現(xiàn)在最后一次加速度突變)，其跟蹤精度甚至好于文獻(xiàn)[14]，與本文算法相當(dāng)。

3.3 仿真實(shí)驗(yàn)三

利用場(chǎng)景3測(cè)試本文算法在模型不匹配情況下的跟蹤能力。各算法均采用勻加速模型跟蹤二維場(chǎng)景下的勻速和勻轉(zhuǎn)彎混合運(yùn)動(dòng)軌跡。過程噪聲協(xié)方差Q=diag[1，1，1，1，1，1]，量測(cè)噪聲協(xié)方差R=diag[100 ,100]，文獻(xiàn)[14]的修正參數(shù)不變。圖7—圖8給出了該場(chǎng)景下標(biāo)準(zhǔn)KF、文獻(xiàn)[14]以及PMKF各算法在x軸和y軸的位置均方根誤差。

由圖7、圖8可知，在模型不匹配的情況下，KF的跟蹤精度比較低，尤其是在狀態(tài)突變的時(shí)候，有明顯的尖峰。文獻(xiàn)[14]通過實(shí)時(shí)修正，較好地改善了模型不匹配情況下的跟蹤精度，狀態(tài)突變時(shí)也具有較強(qiáng)的適應(yīng)能力，誤差曲線相對(duì)比較平滑。但是本文算法具有更明顯的優(yōu)勢(shì)，只在狀態(tài)突變時(shí)有小的波動(dòng)，較好地克服了模型不匹配的影響。

3.4 仿真實(shí)驗(yàn)四

本節(jié)主要是對(duì)所提出的狀態(tài)突變的判決準(zhǔn)則進(jìn)行驗(yàn)證。可調(diào)白噪聲模型是一種典型的通過門限判決來對(duì)濾波器進(jìn)行調(diào)整的機(jī)動(dòng)目標(biāo)跟蹤算法，因此，可以用來測(cè)試門限的優(yōu)劣。選取連續(xù)強(qiáng)機(jī)動(dòng)目標(biāo)(場(chǎng)景4)，量測(cè)噪聲協(xié)方差R=diag[100 ,100]，過程噪聲協(xié)方差在機(jī)動(dòng)時(shí)取Q=diag[1，1，1，1，1，1]，非機(jī)動(dòng)時(shí)取Q=diag[0.005，0.005，0.005，0.005，0.005，0.005]，原始判決門限和本文判決門限分別由式(19)、式(20)給出。圖9—圖10給出了兩種判決門限下對(duì)連續(xù)機(jī)動(dòng)目標(biāo)跟蹤的位置、速度均方根誤差曲線(此處為x、y誤差之和)。

由圖9、圖10易知，本文提出的判決準(zhǔn)則在目標(biāo)發(fā)生連續(xù)機(jī)動(dòng)時(shí)，由于能較好地保持對(duì)機(jī)動(dòng)的檢測(cè)能力，及時(shí)調(diào)整濾波器的參數(shù)，一定程度上降低了峰值誤差，而在非機(jī)動(dòng)段取得與原始算法類似的跟蹤精度。因此，本文提出的判決準(zhǔn)則更為優(yōu)越。

通過以上的四個(gè)仿真實(shí)例，本文所提出的基于后驗(yàn)量測(cè)修正的卡爾曼濾波算法(PMKF)主要的優(yōu)勢(shì)在于：

1)模型匹配時(shí)，通過對(duì)濾波器進(jìn)行微調(diào)，提高穩(wěn)態(tài)時(shí)的跟蹤精度，加快濾波器的收斂速度。

2)在狀態(tài)發(fā)生突變或者模型失配時(shí)，利用后驗(yàn)量測(cè)進(jìn)行實(shí)時(shí)修正，前后兩次用到后驗(yàn)量測(cè)zk+1，增強(qiáng)了對(duì)后驗(yàn)量測(cè)的信任度，起到了漸消因子類似的調(diào)節(jié)作用。

3)與文獻(xiàn)[14]的算法相比，克服了經(jīng)驗(yàn)參數(shù)的設(shè)定，且對(duì)突變狀態(tài)或模型失配的調(diào)節(jié)能力更強(qiáng)。

4)在狀態(tài)連續(xù)變化時(shí)，所提出的判決準(zhǔn)則能保持對(duì)狀態(tài)突變的檢測(cè)能力，及時(shí)修正濾波器，從而取得更高的濾波精度。

4 結(jié)論

本文提出了基于后驗(yàn)量測(cè)修正的卡爾曼濾波算法。該算法通過對(duì)濾波狀態(tài)進(jìn)行實(shí)時(shí)判決，狀態(tài)平穩(wěn)時(shí)采用卡爾曼濾波，狀態(tài)突變時(shí)采用后驗(yàn)量測(cè)卡爾曼濾波算法進(jìn)行修正。理論分析及仿真結(jié)果表明，改進(jìn)的判決準(zhǔn)則能保持對(duì)連續(xù)突變狀態(tài)的檢測(cè)，而后驗(yàn)量測(cè)的修正，不僅提高了穩(wěn)態(tài)時(shí)的跟蹤精度，削弱了狀態(tài)突變帶來的影響，克服了模型失配的缺陷，而且不需要預(yù)設(shè)修正參數(shù)，簡(jiǎn)單實(shí)用，具有一定的工程應(yīng)用價(jià)值。由于卡爾曼濾波器的輸出結(jié)果由預(yù)測(cè)項(xiàng)和修正項(xiàng)兩部分組成，實(shí)際工程應(yīng)用中完全可以既對(duì)預(yù)測(cè)項(xiàng)進(jìn)行修正，也對(duì)修正項(xiàng)進(jìn)行調(diào)整，以取得更好的濾波結(jié)果。如何將二者進(jìn)行合理融合，形成優(yōu)勢(shì)互補(bǔ)是下一步要討論和研究的課題。

[1]RIGATOS G, SIANO P. Control of heat diffusion in arc welding using differential flatness theory and nonlinear kalman filtering [J]. Intelligent Industrial Systems, 2016, 2(1): 5-19.

[2]YU Y. Consensus-Based distributed mixturekalman filter for maneuvering target tracking in wireless sensor networks [J]. IEEE Transactions on Vehicular Technology, 2016, 65(10): 8669-8681.

[3]ZHU W, WANG W, YUAN G. An improved interacting multiple model filtering algorithm based on the cubature kalman filter for maneuvering target tracking [J]. Sensors, 2016, 16(6): 805.

[4]ZHAO Y. Performance evaluation of CubatureKalman filter in a GPS/IMU tightly-coupled navigation system [J]. Signal Processing, 2016, 119(C): 67-79.

[5]周啟帆，張海，王嫣然.一種基于冗余測(cè)量的自適應(yīng)卡爾曼濾波算法[J].航空學(xué)報(bào)，2015，36(5)：1596-1605.

[6]高偉，李敬春，奔粵陽，等.基于多重漸消因子的自適應(yīng)卡爾曼濾波器[J].系統(tǒng)工程與電子技術(shù)，2014(7)：1405-1409.

[7]SAGE A P, HUSA G W. Adaptive filtering with unknown prior statistics [C] //Proceedings of Joint Automatic Control Conference. US: University of Colorado, 1969: 760-769.

[8]XU T H, NAN J, SUN ZZ. An improved adaptive Sage filter with applications in GEO orbit determination and GPS kinematic positioning[J]. Science China Physics, Mechanics & Astronomy, 2012, 55(5): 892-898.

[9]徐定杰，賀瑞，沈鋒，等.基于新息協(xié)方差的自適應(yīng)漸消卡爾曼濾波器[J].系統(tǒng)工程與電子技術(shù)，2011，33(12)：2696-2699.

[10]XIA Q, RAO M, YING Y, et al. Adaptive fadingkalman filter with an application [J]. Automatica, 1994, 30(8): 1333-1338.

[11]柯晶，錢積新.基于邏輯切換的改進(jìn)強(qiáng)跟蹤卡爾曼濾波器[J].電子學(xué)報(bào)，2002，30(6)：925-927.

[12]劉玉磊，馮新喜，鹿傳國(guó)，等.帶漸消因子的Quadrature卡爾曼濾波[J].宇航學(xué)報(bào)，2013，34(10)：1370-1377.

[13]馬云峰.改進(jìn)的強(qiáng)跟蹤卡爾曼濾波器在MSINS/GPS組合導(dǎo)航中的應(yīng)用研究[J].濰坊學(xué)院學(xué)報(bào)，2014，14(2)：1-5.

[14]楊永建，樊曉光，王晟達(dá)，等.基于修正卡爾曼濾波的目標(biāo)跟蹤[J].系統(tǒng)工程與電子技術(shù)，2014，36(5)：846-851.

[15]徐景碩，秦永元，彭蓉.自適應(yīng)卡爾曼濾波器漸消因子選取方法研究[J].系統(tǒng)工程與電子技術(shù)，2004，26(11)：1552-1554.