我們的小學(xué)數(shù)學(xué)課堂可以再慢一點(diǎn)

江蘇省蘇州市吳中區(qū)木瀆姑蘇實(shí)驗(yàn)小學(xué) 蔣 欣

【存在現(xiàn)象】

現(xiàn)象一：有的老師在課堂教學(xué)中（尤其是上公開(kāi)課），課前制作了十分精美的多媒體課件，當(dāng)堂的演示也十分生動(dòng)，整個(gè)展示過(guò)程可以說(shuō)完整又嚴(yán)密，老師本以為這種順風(fēng)順?biāo)恼n堂很好地達(dá)成了預(yù)期的目標(biāo)。可是，課后再請(qǐng)同學(xué)們講述時(shí)，大部分被提問(wèn)的同學(xué)往往是只能反饋其中的只言片語(yǔ)，且講不到本質(zhì)。

現(xiàn)象二：在公開(kāi)課上，老師最擔(dān)心學(xué)生沒(méi)反應(yīng)或者答不出自己心目中的標(biāo)準(zhǔn)答案，“是不是”“對(duì)不對(duì)”幾乎成了口頭禪，而學(xué)生的回答則是一片隨聲附和，“是”、“不是”、“對(duì)”、“不對(duì)”，營(yíng)造出一個(gè)表面熱鬧踴躍的課堂。

現(xiàn)象三：有的老師將“有效課堂”片面地理解為學(xué)生能當(dāng)堂“高效地”完成大量的練習(xí)，于是在一堂課上刻意地組織全體學(xué)生必須完成各種層次的練習(xí)題，這樣程式化地走完教學(xué)設(shè)計(jì)。

【粗淺分析】

上述現(xiàn)象的存在，主要是由于課堂教學(xué)任務(wù)重，知識(shí)點(diǎn)多，而老師片面地追求課堂教學(xué)的“即效”，因此往往不給學(xué)生思辨、動(dòng)手操作的時(shí)間，而是采取“短平快”的問(wèn)答式教學(xué)，如果學(xué)生回答不上來(lái)，教師就自問(wèn)自答——自己將全過(guò)程呈現(xiàn)出來(lái)。或者進(jìn)行高密度的訓(xùn)練，課堂上充滿著計(jì)算公式、解題方法的強(qiáng)化練習(xí)，表面上看課堂容量夠大，學(xué)生短時(shí)間內(nèi)掌握了解題技巧。這種快餐式的教學(xué)，雖然學(xué)生也很積極，但實(shí)際上學(xué)生只是學(xué)習(xí)的機(jī)器，只能盲目地跟著老師的預(yù)設(shè)高速運(yùn)轉(zhuǎn)，其思維主動(dòng)性與創(chuàng)造性并沒(méi)有得到有效發(fā)展。這樣的教學(xué)可能夯實(shí)了“雙基”（基本知識(shí)與基本技能），但是學(xué)生沒(méi)有足夠的時(shí)空去感悟數(shù)學(xué)思想方法，也沒(méi)有有效地積累基本活動(dòng)經(jīng)驗(yàn)。

【幾點(diǎn)嘗試】

教育與其他行業(yè)有著本質(zhì)的區(qū)別：教育不是一蹴而就的，否則就會(huì)“欲速則不達(dá)”，它是一個(gè)讓智慧思考伴隨始終的過(guò)程。然而在我們的小學(xué)數(shù)學(xué)課堂教學(xué)中，依然存在著過(guò)于追求“即效”的現(xiàn)象。下面，筆者結(jié)合自己的幾個(gè)教學(xué)案例談幾點(diǎn)嘗試與思考。

一、課堂慢一點(diǎn)，或許可以收獲“意外的通道”

葉瀾教授曾對(duì)關(guān)于課堂的動(dòng)態(tài)生成說(shuō)過(guò)一句令人回味的話：“課堂應(yīng)是向未知方向挺進(jìn)的旅程，隨時(shí)都有可能發(fā)現(xiàn)意外的通道和美麗的圖景，而不是一切都必須遵循固定線路而沒(méi)有激情的行程。”

我們?cè)谡n堂教學(xué)中，不能急于追求快速到達(dá)“行程”的終點(diǎn)，而要引領(lǐng)學(xué)生漫步于“向未知方向挺近的旅程”，這樣或許會(huì)收獲“意外通道”，領(lǐng)略“美麗圖景”。

如我在教學(xué)“判斷一個(gè)分?jǐn)?shù)能否化成有限小數(shù)”時(shí)，曾偶遇過(guò)這樣的“美麗圖景”。以下是相關(guān)教學(xué)片段：

學(xué)生獨(dú)立完成后反饋，發(fā)現(xiàn)有的分?jǐn)?shù)能化成有限小數(shù)，有的則不能化成有限小數(shù)。教師指出不能化成有限小數(shù)時(shí)，一般保留三位小數(shù)。

生（突然舉手，急于發(fā)言）：如果一個(gè)分?jǐn)?shù)能改寫(xiě)成分母是10、100、1000……的分?jǐn)?shù)，那么它就能化成有限小數(shù)，否則就不能化成有限小數(shù)。（其余學(xué)生沉默片刻后點(diǎn)頭示意）

師：這可是個(gè)重大發(fā)現(xiàn)，真的是這樣嗎？我們?cè)僬規(guī)讉€(gè)分?jǐn)?shù)試試看。

師：看樣子，一個(gè)分?jǐn)?shù)能否化成有限小數(shù)，與它的分母有關(guān)（學(xué)生點(diǎn)頭示意）。那為什么分母是6、14等這樣的分?jǐn)?shù)無(wú)法改寫(xiě)成分母是10、100、1000……的分?jǐn)?shù)呢？

生：像6這個(gè)數(shù)只能擴(kuò)大成30、60、90或者300、600、900等，就是無(wú)法擴(kuò)大為10、100、1000。

生：可能是因?yàn)?里面含有3，所以無(wú)法擴(kuò)大為10、100、1000……這樣的數(shù)。

師（追問(wèn)）：為什么含有質(zhì)因數(shù)3就不能擴(kuò)大成10、100、1000……了呢？

生：因?yàn)樵?0、100、1000……這些數(shù)里只含有質(zhì)因數(shù)2和5。

師：對(duì)今天研究的知識(shí)，我們又有了更新的、更深層的發(fā)現(xiàn)。那么，對(duì)于這兩個(gè)分?jǐn)?shù)，又是誰(shuí)在“作怪”呢？

生：因?yàn)樗鼈兊姆帜钢泻?、3、11這樣的質(zhì)因數(shù)，所以無(wú)法擴(kuò)大為10、100、1000……

師：再看看自己舉例的分?jǐn)?shù)，我們的“發(fā)現(xiàn)”有道理嗎？

學(xué)生通過(guò)驗(yàn)證，無(wú)一例外。

師：既然如此，我們以后判斷一個(gè)分?jǐn)?shù)能否化成有限小數(shù)，是否還要看它能否改寫(xiě)成分母是10、100、1000……的分?jǐn)?shù)，有沒(méi)有更簡(jiǎn)捷的方法？

生（交流后）：不需要改寫(xiě)，只要直接看一個(gè)分?jǐn)?shù)的分母是否含有2、5以外的質(zhì)因數(shù)即可。

生（補(bǔ)充）：如果分母中含有2、5以外的質(zhì)因數(shù)，那么這個(gè)分?jǐn)?shù)就不能化成有限小數(shù)，否則就可以化成有限小數(shù)。

生（再次補(bǔ)充）：這個(gè)分?jǐn)?shù)應(yīng)該是最簡(jiǎn)分?jǐn)?shù)。

……

這完全走出了我原來(lái)的設(shè)計(jì)，也“打亂”了我原有的教學(xué)節(jié)奏，于是我放慢了教學(xué)節(jié)奏，針對(duì)學(xué)生提出的看法進(jìn)行因勢(shì)利導(dǎo)，正是這個(gè)“節(jié)外生枝”，才收獲了這個(gè)探究過(guò)程的“意外通道”。

二、課堂慢一點(diǎn)，可以為學(xué)生的探究而“留白”

在小學(xué)數(shù)學(xué)課堂教學(xué)中，我們提倡引領(lǐng)學(xué)生參與學(xué)習(xí)活動(dòng)，力求體現(xiàn)學(xué)生的主體地位，留給學(xué)生一片自主探究的空間，讓他們經(jīng)歷知識(shí)的發(fā)現(xiàn)、問(wèn)題的提出與思考、規(guī)律的探索、結(jié)論的表達(dá)等活動(dòng)過(guò)程。這就需要我們教師在教學(xué)中學(xué)會(huì)等待，學(xué)會(huì)“留白”，并在“留白”處等待學(xué)生進(jìn)行豐富多彩的自主探究活動(dòng)，在“留白”處讓學(xué)生的探究潛能獲得充分的釋放。

下面以教學(xué)《圓錐體積》為例，談?wù)勛约旱淖龇ā?/p>

圓錐體體積的計(jì)算方法是由圓柱體的體積計(jì)算方法通過(guò)實(shí)驗(yàn)推導(dǎo)得出來(lái)的，其中包含“等底等高”和”兩個(gè)要點(diǎn)。在教學(xué)這一內(nèi)容（推導(dǎo)體積計(jì)算公式）時(shí)，若是簡(jiǎn)單地組織全班同學(xué)看教師的演示實(shí)驗(yàn)，一段時(shí)間后，學(xué)生總是丟三落四。在解決有關(guān)圓錐的實(shí)際問(wèn)題或辨析相關(guān)概念時(shí)，不是忘記比較底和高，就是忘了乘因此，我在教學(xué)這一計(jì)算公式推導(dǎo)時(shí)，放慢了節(jié)奏。首先組織學(xué)生分組實(shí)驗(yàn)，各組中圓柱和圓錐的組合是多樣的——有的等底等高，有的不是等底等高。然后組織實(shí)驗(yàn)操作，實(shí)驗(yàn)后匯報(bào)交流結(jié)果，結(jié)合五花八門(mén)的實(shí)驗(yàn)結(jié)果，反思實(shí)驗(yàn)、尋找原因、發(fā)現(xiàn)聯(lián)系，從而引導(dǎo)學(xué)生發(fā)現(xiàn)：在等底等高的情況下，圓錐的體積時(shí)圓柱體積的這樣，讓學(xué)生親身經(jīng)歷了實(shí)驗(yàn)過(guò)程，他們很容易推導(dǎo)出圓錐的體積公式，有利于防止學(xué)生在計(jì)算圓錐體積時(shí)漏乘這一現(xiàn)象的發(fā)生。各組中不同圓柱圓錐的搭配，又很好地防止學(xué)生認(rèn)為圓錐的體積就是圓柱體積的這一錯(cuò)誤的發(fā)生。

“聽(tīng)過(guò)了，就忘記了；看過(guò)了，就明白了；做過(guò)了，就理解了。”在上述“圓錐體積公式推導(dǎo)”的教學(xué)中，我摒棄了單靠教師演示實(shí)驗(yàn)，學(xué)生觀察、發(fā)現(xiàn)的教學(xué)模式。雖然在課堂上似乎浪費(fèi)了一定的時(shí)間，學(xué)生也少練了幾道題目，但是學(xué)生收獲的不只是一個(gè)抽象的計(jì)算公式，而是明白了計(jì)算公式的由來(lái)，積累了探究幾何圖形計(jì)算公式的基本活動(dòng)經(jīng)驗(yàn)。這一切都需要我們?cè)谡n堂教學(xué)中放慢教學(xué)節(jié)奏，為學(xué)生提供探索的材料，給學(xué)生留下足夠的時(shí)空。

三、課堂慢一點(diǎn)，能使學(xué)生的思考更加深刻

在教學(xué)解決問(wèn)題的策略這一領(lǐng)域的內(nèi)容時(shí)，必須引領(lǐng)學(xué)生經(jīng)歷某種（或幾種）方法來(lái)解決此類問(wèn)題的過(guò)程，而這個(gè)過(guò)程絕不能走過(guò)場(chǎng)，必須實(shí)實(shí)在在地開(kāi)展探索活動(dòng)。這就要求我們?cè)谡n堂上必須給學(xué)生足夠的時(shí)間，學(xué)生才能不斷調(diào)整策略，通過(guò)逐步探索，有效地找到合理的解決問(wèn)題的策略。

下面是筆者關(guān)于六年級(jí)下冊(cè)《解決問(wèn)題的策略——假設(shè)》的處理方法。

教學(xué)例題時(shí)，我放手讓學(xué)生進(jìn)行猜測(cè)——可能有幾只大船？幾只小船？結(jié)合學(xué)生的猜測(cè)，整理成下表：（每只大船做5人，每只小船做3人）

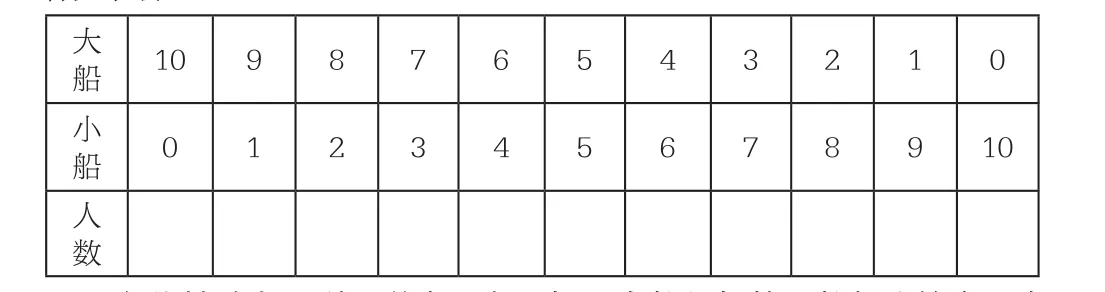
大船 10 9 8 7 6 5 4 3 2 1 0小船 0 1 2 3 4 5 6 7 8 9 10人數(shù)

在此基礎(chǔ)上，引導(dǎo)學(xué)生思考：如果人數(shù)與船的只數(shù)都比較多，有沒(méi)有什么好的方法？學(xué)生提出可以假設(shè)大船與小船各一半，可以2只2只、3只3只甚至5只5只隔著調(diào)整。我在組織反饋、引導(dǎo)驗(yàn)證、給予肯定的基礎(chǔ)上，再次提出：還有沒(méi)有別的方法呢？于是就有了下面的教學(xué)片段：

師：我們?cè)倏春诎迳系谋砀瘢僭O(shè)租的都是大船時(shí)，能坐幾個(gè)人？

生：50人。

師：實(shí)際呢？和實(shí)際人數(shù)相比，發(fā)生了什么變化？

生：多了8個(gè)人。

師：怎么會(huì)多了8個(gè)人呢？

生：因?yàn)榘哑渲械囊恍┬〈?dāng)成了大船，所以能坐的人就多了。

師：那么1只小船當(dāng)成1只大船，就會(huì)多坐幾個(gè)人呢？

生：2人。

師：那么多了8個(gè)人，說(shuō)明有幾只小船呢？

教師一邊引導(dǎo)一邊列式：（學(xué)生敘述每個(gè)算式的含義）5×10＝50（人），50－42＝8（人），8÷（5－3）＝4（只）。

師（上述方法驗(yàn)證后）：如果假設(shè)全是小船，你能解決嗎？

……

可見(jiàn)，我們的課堂教學(xué)需要慢一點(diǎn)。課堂慢一點(diǎn)，多給學(xué)生一次“異想天開(kāi)”的機(jī)會(huì)，我們的課堂探究或許會(huì)收獲一個(gè)“意外的通道”；課堂慢一點(diǎn)，多給學(xué)生一次動(dòng)手操作的機(jī)會(huì)，我們教學(xué)目標(biāo)的達(dá)成度就會(huì)更高；課堂慢一點(diǎn)，多給學(xué)生一次思辨的機(jī)會(huì)，學(xué)生的思維就會(huì)走向更深處。