開放題：筑起“空間想象”的新時空

仲崇恒

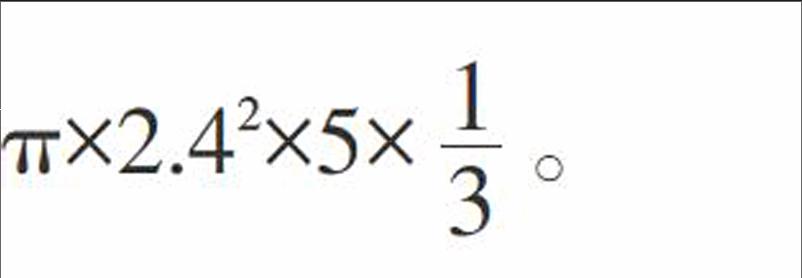
數學能力是數學教育的重要課程目標，空間想象能力是傳統的三大數學能力之一。筆者在開放題評測研究中發現，開放題對學生空間想象能力有著較為直接而積極的影響，開放題教學是培養小學生空間想象能力的一條有效路徑。培養學生空間想象能力，材料有很多，如圖形的轉換、分解、組合、辨認、概括、推理、計數、展開和折疊等。下面結合幾個教學實例，來說說開放題對小學生空間想象能力培養的影響。

一、開放題，為“空間想象”奠定基石

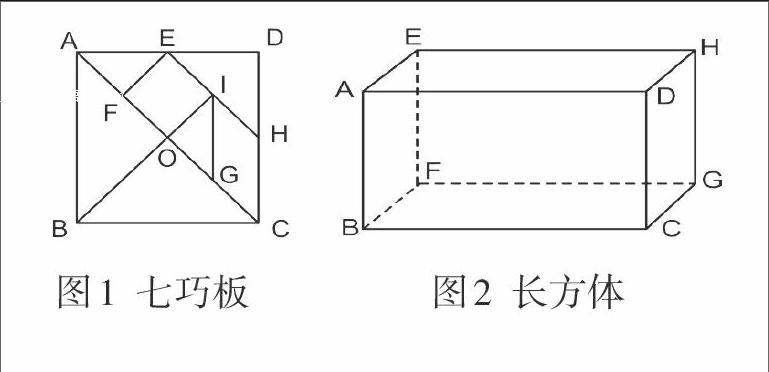
“平行和垂直”教學時，教師設計這樣一道同步練習：在下列圖形中，哪兩條線段是相互平行的？哪兩條線段是相互垂直的？

出示圖1，學生小組合作探究交流后，教師追問學生有什么發現？有的發現一條直線和一組平行線的其中一條直線垂直，也與另一條直線垂直；有的發現與同一條線段垂直的兩條線段是互相平行的。出示圖2時，學生逐一審視長方體的十二條棱間所構成的平行或垂直。回顧圖1中的發現，就有學生在圖2中找到反例，從而進一步認同了“同一平面”這個判斷前提。二維和三維之間的相互轉換，恰是發展學生空間觀念的有益舉措。

一個好的開放題不是條件的多余或缺少的簡單取舍，也不是問題的一而再、再而三的無序提出。開放題設計首先是從教學內容的核心知識出發，尋找思維訓練的落腳點。上面習題富含空間想象元素，隱含多重維度，多種可能，相比傳統的封閉習題，開放題如同一塊堅實的基石，穩定性和延伸性更好，可以承載全體學生各種空間思維的不同建構。

二、開放題，為“空間想象”豎起腳手架

“長方體和正方體”單元復習時，教師課件呈現：

倉庫里有以下四種規格的長方形、正方形鐵皮。①長6分米，寬4分米；②長6分米，寬5分米；③長5分米，寬4分米；④邊長4分米。張師傅從中選了5張鐵皮，焊接成一個無蓋的長方體（或正方體）水箱。你能描述一下這個水箱嗎？

學生獨立思考和集體交流后，教師問：怎樣找出更多的，甚至所有的情況？有的學生認為：四種不同規格鐵皮中有6分米、5分米、4分米三種數據，這也是焊成的水箱長寬高的長度。可以分別考慮長寬高中有三種數，或兩種數，或只有一種數。有的學生認為：先定底面再選側面，側面的長方形鐵皮和底面相連的地方長度相同。教師引導學生思考：第一種先定長寬高，第二種先定底面，兩種思路都是從簡到繁。接著繼續探究，師問：請選擇你能理解的一種思路，試一試能焊出幾種不同的水箱。第二次深入交流后，教師引導：回顧過程，我們的思考和表達怎樣改進才能更清晰呢？

本題條件多，答案也多，屬于典型的條件和答案雙開放習題。學生的不同思路呈現了兩種不同的思維視角，共同點是都是從“體”出發，然后進行材料匹配。學生為了讓頭腦中的“體”可視化，搭建了一個個結結實實的思維腳手架，學生經歷多途徑、多層次的篩選、比對，通過獨立思考和自主探究，理解棱、面、體之間的密切聯系，進一步涵養了空間想象能力。

三、開放題，為“空間想象”架起立交橋

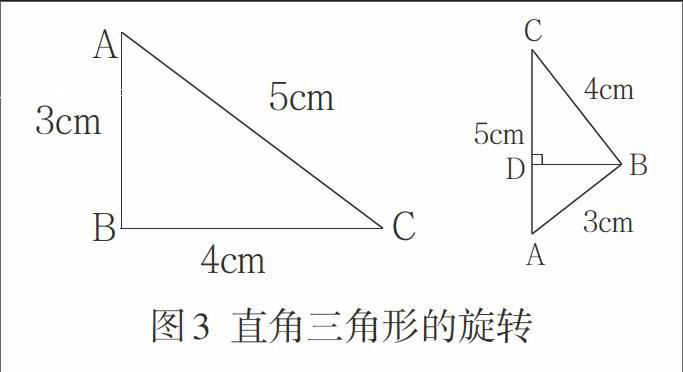
“圓錐的體積”教學時，教師出示：以直角三角形（圖3）的一條邊為軸，將三角形旋轉一周，可以得到一個什么體？試一試畫出來，然后計算它的體積。

“掌握旋轉體”是中小學生空間想象能力水平的最高級。三角形有三條邊，旋轉后有三種情況，其中以斜邊AC為軸的旋轉體思維難度最大。學生通過想象，畫圖，討論，交流，解決了以AB、BC兩直角邊為軸旋轉后圓錐體積的情況。

教師：以AC為軸可以嗎？想象一下能得到一個怎樣的立體圖形？誰能用橡皮泥把它捏出來？

兩名學生捏泥，集體修正、展示后，全體學生畫旋轉示意圖，并找出半徑和高的數據。

教師：半徑BD和旋轉軸AC是什么關系？

學生講解：線段BD與AC垂直，半徑是2.4厘米。

教師：上下兩個圓錐的高又各是多少呢？

學生講解：不需要求出兩個高。兩個圓錐半徑相同，底面積相同，可以合二為一，整體考慮，組合體的體積就是

上面教學中，師生互動，生生聯通。整個開放題處理呈現一種立交橋結構：首先是方法孵化的立體思維。教師在學生思維遇到阻礙時，停下來，從動手捏泥到畫示意圖，再到聯想推理，由淺入深，步步提升。其次是伙伴式的立體學習。學生們呼朋引伴，互相啟發，用團隊思考提升思維品質。

在空間想象能力的培養中，圖形與幾何是十分重要的領域，同時在數與代數、統計與概率等領域也有用武之地。比如，乘法分配律，行程問題，平均數，折線統計圖等。我們認為，教與學中首先有想象的空間，然后才有空間想象。不同的學生面對一道數學題，應該有不同的思維打開方式。開放題教學不僅要在開放題的條件、問題、情境設計上下功夫，還要開放地教，開放地學。我們應該圍繞這些方面進一步展開多元思考，設計出更有張力的開放題，探索更有親和力的教學流程，幫助學生更好地理解數學，發展數學素養。

（作者單位：江蘇省昆山市玉峰實驗學校）