MPCK視角：促進兒童深度學習數學

作者簡介

劉曉萍，女，中學高級教師，蘇州市中小學數學學科帶頭人，現任蘇州市教育科學研究院小學數學教研員，多次參與蘇教版小學數學教材的編寫，曾在《江西教育》《中小學教師培訓》《課程教學研究》《今日教育》等多家期刊發表數十篇論文，其中多篇論文被人大復印中心全文轉載或者索引。

所謂MPCK，即是教師關于特定數學內容如何組織、表征和調整以適應學習者不同興趣和能力，從而進行有效教學的知識。鮑銀霞教授調查得出：“小學數學教師在內容維度上最為薄弱，教學維度和學生維度上存在許多亟待解決的問題。”一語中的，我們數學老師唯有不斷提高自己的MPCK，才能實現克萊因所期望的“高觀點下的初等數學教學”，才能幫助學生通過深度學習，促進思維的發展。

一、內容維度：從招式走向專業

王永春老師曾在一次報告中說讀懂教材是教師的基本功。專業化的數學內容解讀，就是要求教師用全方位、立體化的視角去鉆研教材，掌握每一節課教學內容“是什么”“為什么”，了解它在板塊中的位置、意義、作用，與其他內容的縱聯關系，依照知識的邏輯性、系統性、連貫性的順序，實現教學內容的新舊聯系、從低到高、螺旋上升，以知識序確定教學序并確定教學目標、教學素材、教學活動、輕重詳略。

比如“認識乘法”，是在學生理解了加、減法的含義，掌握了100以內加、減法運算的基礎上安排的。另外，乘法運算作為四則運算之一，它是進一步學習除法運算和解決相關實際問題的直接基礎。學生建立乘法的概念，需要結合實例，通過觀察、操作、比較、分析、抽象、概括等具體活動，從豐富的感性材料中抽象出“求幾個幾相加→加法算式→兩道乘法算式”，進而初步理解乘法概念的含義。

而概念的引入需要提供大量的感性材料，乘法亦是如此。教材增加了“兔有幾個2只？雞有幾個3只？”的問題，是為了進一步凸顯“幾個幾相加”的抽象過程，逐步把握乘法概念的本質屬性，實現認知飛躍，既完成了乘法概念的自主建構，又初步感悟了數學抽象的過程，積累了教學活動經驗，也使數學教學真正由“雙基”向 “四基”轉變。

同時，概念的建構需要安排豐富的認知體驗。教學時，一方面要通過典型實例，使學生知道“求幾個相同加數的和，可以用乘法計算”，另一方面要適當增加問題情境的復雜性，使學生真切感受到有些“求幾個相同加數的和”的問題用乘法計算比較簡便。獲得這樣的體驗，不但可以幫助學生深刻感受乘法運算的學習價值，而且有助于學生體會乘法和加法的聯系，加深對乘法的認識。

概念的內化還需要組織有層次的練習。學生通過看一看、擺一擺、想一想、填一填等具體的活動，獲得對乘法意義的豐富感知，體會加法與乘法之間的聯系，把握乘法概念的本質。

再如“分數”的教學，若要使學生切實理解分數運算規則，兒童必須先行掌握分數的以下七個特性：1.沒有一個可以分割的整體，就不可能有分數的思想。2.一個分數蘊含著一定數目的部分，定量的分配是以分成的人數必須與享受者的數目相一致為條件的。3.一個確定的分數的第三個特點是完全的劃分，即沒有剩余的部分。4.整體所分成的份數和分割的次數之間存在著固定的關系。5.算術上的分數概念意指各個部分都是相等的。6.它們都是原來整體的部分，同時本身也是一個能夠進一步再分的整體，它們形成一個構造的序列。7.分數是與它所來自的整體相聯系的，整體保持著不變性。

二、學生維度：從釋然走向實然

1. 情境導心

創設合適情境是促進學生深度學習的一個關鍵。因為數學問題情境的創設，一是基于對核心素養的理解與認識，二是為了激發內在動機，讓學習任務對人的學習能力引起挑戰。

“倍的認識”一課，徐斌老師創設了這樣一個情境：

師：春暖花開，同學們來到學校花壇。花壇里開滿了鮮花。圖中有哪幾種顏色的花？你能分別數數有幾朵嗎？

生1：有藍、黃、紅三種顏色的花。

生2：藍花有2朵 ……

師：根據這些已知信息，你能提出哪些數學問題？

師：同學們提出的問題都很有道理。其中，不少同學提出了比較兩種花多少的問題，也就是求兩個數量相差多少。其實，比較兩個數量除了我們已經學過的求相差多少，還有另一種方法——倍。

倍的知識來源于比較。從“差比”到“倍比”，是學生認識上的一個飛躍，需要教師從學生的認知特點出發，引領學生從舊知起步逐步學習新知。同時，讓學生面對三種花的數量，自己提出數學問題，培養學生的問題意識，發展學生的數學思考。

2.明理促思

數學教學處處皆有道理，教學要做到有理可循、有理有據，才能將數學學習引向深入。教師應當對數學知識的產生、性質以及結構有所了解和掌握，理解數學知識的內涵，引領學生追溯數學知識的本源，讓學生理解數學知識本質之理，讓學生感受到這樣的數學道理是可以理解的。

比如，關于負數在現實生活中有很多原型。“認識負數”一課的導入，是選擇“溫度計”還是“負債”模型，粗看上去差不多，前者是從負數在生活中的應用來引入，而后者是從負數的發展史來引入。東方數學最早接受負數，是因為他們需要解決生活中具有相反意義的量的實際問題，像收入、支出、盈余、不足都自然地具有相反意義的量，因此，利用它們能很自然地理解負數的意義。

3.體驗積智

學生在數學學習過程中的觀察、實驗、傾聽、思考等均屬于深度體驗的學習方式。一如老師們常用的數學實驗，便是小學數學課堂研究數學問題的良好體驗方法，學生借助直觀操作和形象描繪，做學玩合一，思創行一體，在體驗數學知識從具體逐漸走向抽象的過程中，理解相關的數學原理，發展學科素養。

當然，積累了一定的思維活動經驗，又有可能會阻礙進一步的數學學習。在一節公開課上，鄒柯老師問學生：“1、2、3、4、5是什么數？”學生說“整數。”老師續問：“還是什么數？”學生說：“自然數。”老師再問：“還是什么數？”學生茫然不知如何作答，老師兩次提示 “正……”學生仍然答不出“正整數”。這是什么原因？原來學生把自然數分為正整數、整數、0。不過，教學中為什么學生很難意識到這樣的分類是錯誤的？學生把自然數分為正整數、整數、0，有什么樣的價值？原來，學生的數學啟蒙，大多是從學數1、2、3開始，待掌握了9、10之后才回過頭來認識0，何況學習1、2、3等數的時間遠遠多于學習0的時間，因此學生在多年的強化中，將0排斥在了整數之外。還有，學生很少接觸負數，心理上抵觸-1、-2等數也屬于整數，在很長一段時間里，學生理所當然地認為整數就是正整數。因此課堂教學中，老師總要為知識的生長埋下一些種子，例如0與1、-1的同步認識，這些種子知識可能學生暫時有困惑，但困惑何嘗不是求知的原動力，何嘗不是將來某個知識點的支點。endprint

三、教學維度：從經驗走向理性

1.教學設計視野寬

基于深度學習的教學設計，既要體現立德樹人的育人理念，更要彰顯數學學科的魅力，也就是凸顯“兒童基點，學科視野”這兩大特點，體現教學內容所承載的實用價值、理性價值（數學素養的核心）和發展價值。正是因為這些獨特且豐富的育人價值開發，學科教學才有可能生成豐富而又多元的資源，學生的精神世界的發展才有可能從中獲得多方面的滋養，才有可能不斷豐富和完善自己的生命世界。

如：在沒有括號的四則混合運算中為什么要先乘除后加減，可能是很多老師也說不清的。訪談得到的答案一般有兩種，一是認為是規定，二是認為乘除法是加減法的高級形式，所以要先乘除后加減。其實兩種說法都沒有道出運算順序的本質。要讓學習真正發生，如果我們教學的內容都沒有真正理解，結果可想而知。四則混合運算順序這種“規定”的背后有深刻的道理，有數學的思想和方法。那我們的教學就要讓學生明白這樣的道理，觸摸“規定”，感悟這知識背后的思想和方法，這樣的學習才是深入的。

可以看出，四則混合運算的教學關鍵是讓學生理解運算順序并了解它的由來，教學的重點是指向算理的深度理解，教學的目標是發展學生的運算能力，要讓學生依據自身的生活經驗和已有知識，探索并“創造”出四則混合運算的“序”，讓“序”有理，讓“序”有型，讓“序”有值，從而實現讓學習真正發生的目標。

2.核心問題引領探究

著名數學家P. Harmous 強調“問題是關鍵”，數學概念、定理、模型和應用都是在解決問題的過程中總結形成的。在數學課程目標中，特別強調發展學生發現問題、提出問題與分析解決問題的能力，在基于數學核心素養的深度學習中，這也是關注的重點。

例如“近似數”一課，教師設計了這樣三個核心問題：“為什么要有近似數？什么是四舍五入？怎么運用近似數？”在層層遞進式的核心問題引領下，學生經歷猜想、驗證、交流的過程，發展了數學思維，并獲得良好的、積極的情感體驗。

3.評價多元化

指向數學學科本質的評價既要關注學生學習的結果，也要重視學生經歷深度學習的過程，即不僅考查對知識與技能的掌握情況，而且注重考查學生對其中所蘊涵的數學本質的理解，更多地關注對數學方法、思想本身的理解，以及在理解基礎上具體情境中的合理運用。

教學中，可以關注學生“對數學學習持久的興趣”，并從以下方面進行評價：（1）喜歡學習數學，對數學學習擁有好奇心；（2）喜歡探求新問題，對學習內容高度關注；（3） 能用數學的眼光來關注生活，從生活世界中捕捉數學問題。學生“數學應用能力”可從以下方面進行評價：（1）能靈活掌握所學知識，對相關知識能夠理解和熟記；（2）能結合具體的情境，有依據地進行合情的推理和判斷；（3）能應用所學知識靈活解決實際問題。

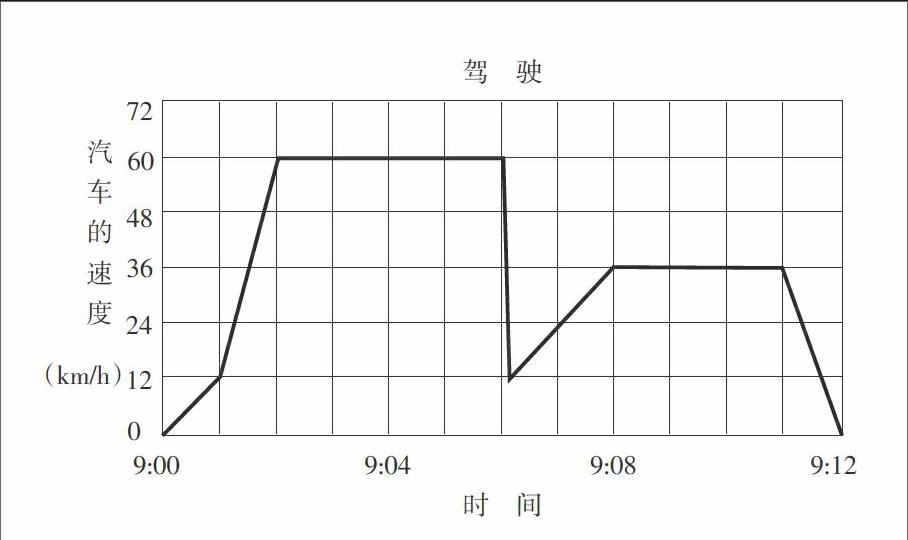
以考查學生數據分析能力為例，可以設計如下問題情境：李紅的爸爸開車出門，在駕駛期間，一只貓跑到了汽車前面。他猛踩剎車，躲過了那只貓，但心里有點受驚的感覺，于是決定回家。下圖簡略地記錄了李紅的爸爸駕駛期間汽車的速度。

（1）在李紅的爸爸駕駛期間，汽車的最大速度是多少？

（2）為了躲避那只貓，爸爸猛踩剎車的時間點是多少？

（3）爸爸回家的路程，跟他出門的距離一樣嗎？利用圖表中所給的信息，寫出一個解釋來說明你的答案。

人們追求可靠性、確定性的時候，只剩下一塊安寧的綠洲，就是數學。但長期以來，數學看重知識的邏輯結構和形式化體系，加之數學課程在“應試”中所占有的重要地位，使得“解題”一度成為數學教學的首要目標，這種“見數不見人”的數學學習觀在實踐中已經形成諸多弊端。教育就其本質來說“是人生存的需要，教育是主動的行為，每個人都有受教育的欲望”。因此，學生的深度學習挑戰著數學教師對MPCK的深度理解。

（作者單位：江蘇省蘇州市教育科學研究院）

□責任編輯 李杰杰

E-mail：731836457@qq.comendprint