高中數學變式題組訓練一
——初高中教材銜接代數部分復習

山西 李有貴 廣東 朱 歡 安徽 郭洪利 江蘇 王懷學

高中數學變式題組訓練一
——初高中教材銜接代數部分復習

山西 李有貴 廣東 朱 歡 安徽 郭洪利 江蘇 王懷學

1.數域的擴充：數的分類;二次根式；有理化因式;

2.式子的運算：合并同類項與通分;多項式恒等對應項系數相等;利用恒等式將分式裂項;

3.多項式乘法與分解因式：立方和差公式;完全立方和差公式;十字相乘法;

4.一元二次方程的根：判別式;韋達定理;

5.方程組：二元一次方程組；二元二次方程組;

6.二次函數：解析式的待定系數求法;最值與變化趨勢;平移變換;對稱變換.

【題組訓練】

1．數域的擴充

1.1 數的分類

【典例】判斷下列說法正確的是________.

(1)0是既不是正數也不是負數；

(2)0不是自然數；

(3)-1是負數，但不是整數，更不是奇數；

(4)2是最小的質數；

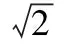
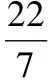
(7)方程x2+1=0沒有實數根.

【解析】實數分為正數、負數、零，因此(1)正確；

由于計數的需要，就產生了1，2，3，4等數以及表示“沒有”的數0，都是自然數，(2)錯誤；

能被2整除的整數是偶數，如2，0，-2，…，記為2k(k為整數)，不能被2整除的整數是奇數，如-1，1，3，…，記為2k+1(k為整數).-1是負整數，也是奇數，(3)錯誤；

如果一個大于1的正整數，只能被1和它本身整除，那么這個正整數叫做質數(素數)，如2,3,5,7,11,13,17,19，…，如果一個正整數能被1和它本身除外的正整數整除，那么這個正整數叫做合數，(4)正確；

因為x2≥0，所以方程x2=-1沒有實數根，(7)正確．

因此(1)(4)(7)正確．

【變式】判斷下列說法正確的是

(1)正整數是正數也是實數；

(2)自然數都是正整數；

(3)整數可以分為奇數和偶數；

(4)質數都是正整數；

(5)小數都是無理數；

(6)有的無理數是分數.

1.2 二次根式

【典例】求值．

(1)9的平方根；(2)125的立方根；(3)27的3次方根；(4)-32的5次方根；(5)16的4次方根．

【解析】(1)因為(±3)2=9，則±3是9的平方根．

(2)53=125，則5是125的立方根．

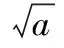
【變式】

1.若x2=25,則x=________．

2.若(x-2)2=16,則x=________．

3.若x4=25,則x=________．

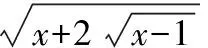
1.3 有理化因式

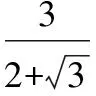
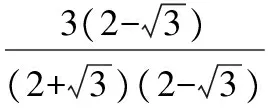
【變式】

( )

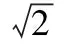
A.alt;blt;cB.alt;clt;b

C.blt;alt;cD.blt;clt;a

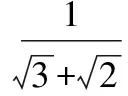
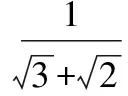
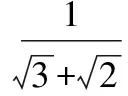
對于甲，乙兩位同學的解法，其中做的正確是________．

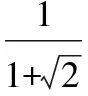
2．式子的運算

2.1 合并同類項與通分

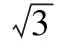
(2)2-22-23-24-25-…-218-219+220.

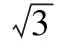
(2)因為2n+1-2n=2n,

所以，原式=2-22-23-24-25-…-218+219=2-22-23-24-25-…+218=……=2+22=6.

【變式1】

1.若x2+mx-10=(x+a)(x+b),其中a,b為整數，則m的值為

( )

A．3或9 B．±3

C．±9 D．±3或±9

3.多項式(x+1)(x+2)(x+3)·…·(x+2 016)的常數項為________，其多項式的次數是________；最高次項系數是________．

4.定義：i2=-1，則將(1-i)(1+2i)2利用乘法法則，表示為p+qi(p,q是實數)的形式，則p+q=________．

5.已知i2=-1，類比多項式的乘法計算

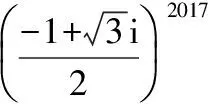
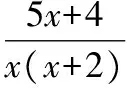
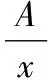
【變式2】

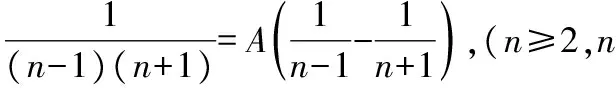
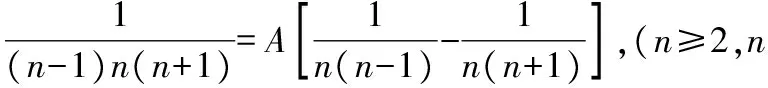
2.2 多項式恒等對應項系數相等

【典例】已知兩個多項式kx+b，k(kx+b)+b在實數范圍內，不論x取什么實數值代入兩式總是相等的，求k,b的值．

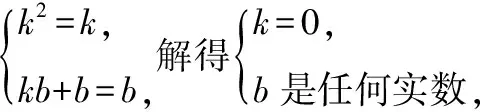
【評注】多項式恒等的定義：設f(x)和g(x)是含相同變量x的兩個多項式，f(x)≡g(x)表示這兩個多項式恒等．就是說x在取值范圍內，不論用什么實數值代入，等式總是成立的．符號“≡”讀作“恒等于”，也可以用等號表示恒等式．例如：(x+3)2=x2+6x+9,5x2-6x+1=(5x-1)(x-1),x3-39x-70=(x+2)(x+5)(x-7)都是恒等式，這些式子展開后對應項相等．

【變式】

1.已知x2-3x-a2=(x-3)(x+b)，在實數范圍內，不論x取什么實數值，式子總是成立的，則a+b=________．

2.已知x3-3x-2=(x+m)(x2+nx-2)，在實數范圍內，不論x取什么實數值，式子總是成立的，則mn=________．

3.已知a(x+1)2+b(x+1)+c=ax2+(2+b)x+c+1，在實數范圍內，不論x取什么實數值，式子總是成立的，求a,b的值．

2.3 利用恒等式將分式裂項

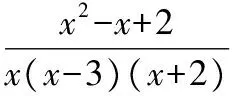
【解析】

x2-x+2=A(x-3)(x+2)+Bx(x+2)+Cx(x-3)

=A(x2-x-6)+Bx2+2Bx+Cx2-3Cx

=(A+B+C)x2+(-A+2B-3C)x-6A．

【變式】

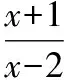
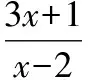
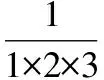
3.多項式乘法與分解因式

3.1 立方和差公式

【典例】計算：

(1)(4+m)(16-4m+m2);

【解析】(1)原式=43+m3=64+m3;

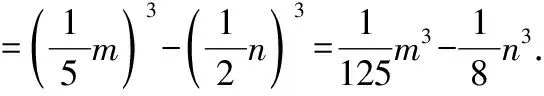
【評注】立方和公式(a+b)(a2-ab+b2)=a3+b3；立方差公式(a-b)(a2+ab+b2)=a3-b3．

平方差公式(a+b)(a-b)=a2-b2；完全平方公式(a+b)2=a2+2ab+b2；(a-b)2=a2-2ab+b2；(a+b+c)2=a2+b2+c2+2(ab+bc+ac).

【變式】

1.計算(1)(3x-2y+1)(3x+2y-1)；(2)(3a+2b+1)(3a-2b+1)；(3)(3x+y+1)(3x-y-1).

2.計算(1)(3x-2y+z)2；(2)(x-1)(x-2)(x-3)·(x-4).

3.2 完全立方和差公式

【典例】計算(x-y)3.

【解析】(x-y)3=(x-y)2(x-y)=(x2-2xy+y2)(x-y)=x3-x2y-2x2y+2xy2+xy2-y3=x3-3x2y+3xy2-y3.

【評注】兩數和的立方公式(a+b)3=a3+3a2b+3ab2+b3;

兩數差的立方公式(a-b)3=a3-3a2b+3ab2-b3.

【變式】計算(1)(x-2y)3；(2)(x+2)4.

3.3 十字相乘法

【典例】把a1a2x2+(a1c2+a2c1)x+c1c2分解因式．

【解析】a1a2x2+(a1c2+a2c1)x+c1c2=a1a2x2+a1c2x+a2c1x+c1c2=a1x(a2x+c2)+c1(a2x+c2)=(a1x+c1)(a2x+c2).

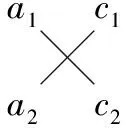
這種借助畫十字交叉線分解系數，從而將二次三項式分解因式的方法，叫做十字相乘法．

必須注意，分解因數及十字相乘都有多種可能情況，所以往往要經過多次嘗試，才能確定一個二次三項式能否用十字相乘法分解．

【變式】

1.將下列多項式因式分解：

(1)12x2-5x-2；(2)12x2-23x-2;(3)12x2-25x+2；(4)12x2-11x+2.

2.將下列多項式因式分解：

(1)15x2-2xy-8y2；(2)15x2+14xy-8y2；(3)15x2-7xy-8y2；(4)15x2+19xy-8y2；(5)15x2-19xy-8y2；(6)15x2+2xy-8y2．

4．一元二次方程的根

4.1 判別式

【典例】討論一元二次方程ax2+bx+c=0(a≠0)的根的情況.

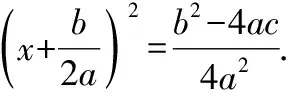
因為a≠0，所以，4a2gt;0．于是

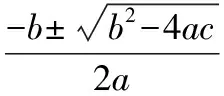
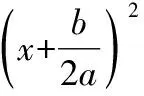
【變式】判定下列關于x的方程的根的情況(其中a為常數)，如果方程有實數根，寫出方程的實數根．(1)x2-ax+(a-1)=0；(2)x2-2x+a=0．

4.2 韋達定理

【典例】已知：x1,x2為一元二次方程ax2+bx+c=0(a≠0)的兩個根，

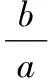
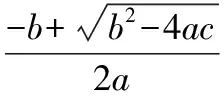
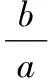
【變式】

1．若方程2x2-4x-3=0的兩根為α,β，則α2-2αβ+β2=________．

2.設x1,x2是方程2x2-4x-3=0的兩個根，則(x1+1)(x2+1)=________.

3.已知方程5x2+kx-6=0的一個根是2，求它的另一個根及k的值．

4.已知兩個不等實數m,n滿足m2-2m=a,n2-2n=a,m2+n2=5，求實數a的值.

5.已知對于任意實數a關于x的方程x2+(a-1)x+ab-2=0都有兩個不相等的實數根，求實數b的取值范圍.

5.方程組

5.1 二元一次方程組

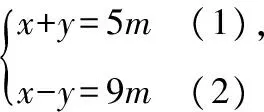
【解析】(1)+(2)得2x=14m，所以x=7m.

(1)-(2)得2y=-4m,所以y=-2m.

把x=7m,y=-2m代入方程2x-3y=9得

2×7m-3×(-2m)=9,

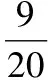
【評注】1．加減消元法：將一個(或兩個)方程兩邊同乘以一個數,使得某一個未知數的系數相等或互為相反數，再將得到的方程相加(減)就可以消去一個未知數，得到一個一元一次方程.這種解二元一次方程組的方法叫做加減消元法，簡稱加減法．

2．代入消元法：解方程組的基本思路是“消元”．即把“二元”變為“一元”，主要步驟是：將其中一個方程中的某個未知數用含有另一個未知數的代數式表示出來，并將其代入另一個方程中，從而消去一個未知數，化二元一次方程組為一元一次方程.這種解方程組的方法稱為代入消元法，簡稱代入法．

【變式】

5.2 二元二次方程組

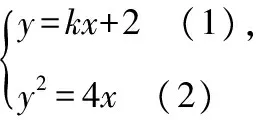
【解析】(1)代入(2)得(kx+2)2=4x,

即k2x2+4(k-1)x+4=0,

當k=0時，方程為一元一次方程，有一解x=1，y=2;

【評注】(1)解由一個二元一次方程和一個二元二次方程組成的方程組的步驟：

①由二元一次方程變形為用x表示y的方程，或用y表示x的方程(3)；

②把方程(3)代入二元二次方程；

③解消元后得到的一元二次方程；

④把一元二次方程的根，代入變形后的二元一次方程(3)，求相應的未知數的值；

⑤寫出答案．

(2)消x，還是消y，應由二元一次方程的系數來決定．若系數均為整數，那么最好消去系數絕對值較小的.

(3)消元后，求出一元二次方程的根，應代入二元一次方程求另一未知數的值，不能代入二元二次方程求另一未知數的值，因為這樣可能產生增根，這一點切記．

【變式】

6．二次函數

6.1解析式的待定系數求法

【典例】已知二次函數的圖象過點(-3，0)，(1，0)，且頂點到x軸的距離等于2，求此二次函數的表達式．

【解析】(法1)因為二次函數的圖象過點(-3，0)，(1，0)，

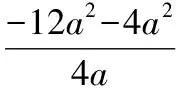
【評注】二次函數有三種形式：1．一般式：y=ax2+bx+c(a≠0)；2．頂點式：y=a(x-h)2+k(a≠0)，其中頂點坐標是(h,k)；3．交點式(兩根式)：y=a(x-x1)(x-x2)(a≠0)，其中x1,x2是二次函數圖象與x軸交點的橫坐標．根據已知條件確定二次函數解析式，通常利用待定系數法．用待定系數法求二次函數的解析式必須根據題目的特點，選擇適當的形式，才能使解題簡便．一般來說，有如下幾種情況：

1．已知拋物線上三點的坐標，一般選用一般式；

2．已知拋物線頂點或對稱軸或最大(小)值，一般選用頂點式；

3．已知拋物線與x軸的兩個交點的橫坐標，一般選用兩根式；

4．已知拋物線上縱坐標相同的兩點，常選用頂點式．

【變式】

1.已知某二次函數的最大值為2，圖象的頂點在直線y=x+1上，并且圖象經過點(3,-1)，求二次函數的解析式．

2.已知二次函數的圖象過點A(-1,-22),B(0,-8),C(2,8)，求此二次函數的表達式．

6.2 最值與變化趨勢

【典例】某產品每件成本10元，試銷階段每件產品的銷售價x(元)與產品的日銷售量y(件)之間的關系如下表：

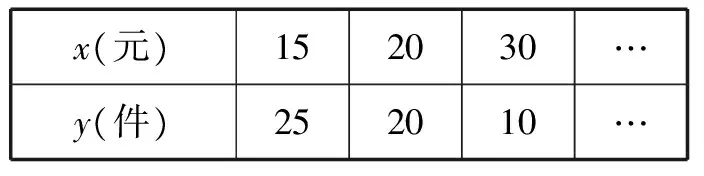
x(元)152030…y(件)252010…

若日銷售量y是銷售價x的一次函數．

(1)求出日銷售量y(件)與銷售價x(元)的函數關系式；

(2)要使每日的銷售利潤最大，每件產品的銷售價應定為多少元？此時每日銷售利潤是多少元？

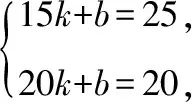
(2)設每件產品的銷售價應定為x元，所獲銷售利潤為w元,

則w=(x-10)(40-x)=-x2+50x-400=-(x-25)2+225，

產品的銷售價應定為25元，此時每日獲得最大銷售利潤為225元．

【變式】

1.二次函數y=x2-4x-7的最小值是

( )

A．-11 B．7

C．11 D．-3

( )

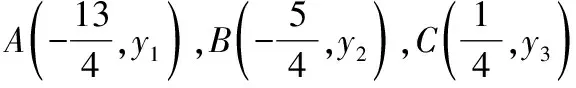
A．y1lt;y2lt;y3B．y2lt;y1lt;y3

C．y3lt;y1lt;y2D．y1lt;y3lt;y2

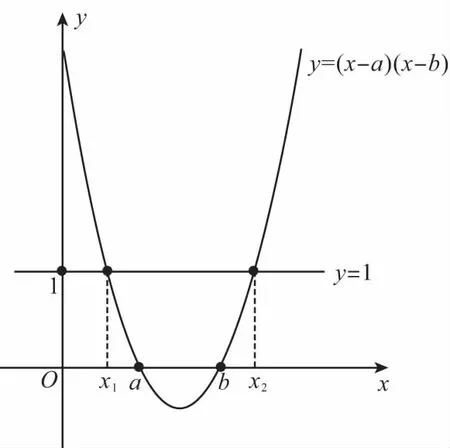
3.若x1,x2(x1lt;x2)是方程(x-a)(x-b)=1(alt;b)的兩個根，則實數的大小關系為

( )

A.x1lt;x2lt;alt;bB.x1lt;alt;x2lt;b

C.x1lt;alt;blt;x2D.alt;x1lt;blt;x2

4.已知二次函數y=-x2+bx+3的圖象的對稱軸是x=-2，則該函數的最大值是________．

5.已知拋物線y=-2(x+3)2-1，如果y隨x的增大而減小，那么x的取值范圍是________．

6.關于x的一元二次方程ax2-3x-1=0的兩個不相等的實數根都在-1和0之間(不包括-1和0)，則a的取值范圍是________.

6.3 平移變換

【典例】求把二次函數y=2x2-4x+3的圖象經過下列平移變換后得到的圖象所對應的函數解析式：

(1)向右平移2個單位，向下平移1個單位；

(2)向上平移3個單位，向左平移2個單位．

【解析】二次函數y=2x2-4x+3的解析式可變為y=2(x-1)2+1，其頂點坐標為(1，1)．

(1)把函數y=2(x-1)2+1的圖象向右平移2個單位，向下平移1個單位后，其函數圖象的頂點坐標是(3，0)，所以，平移后所得到的函數圖象對應的函數表達式就為y=2(x-3)2．

(2)把函數y=2(x-1)2+1的圖象向上平移3個單位，向左平移2個單位后，其函數圖象的頂點坐標是(-1，4)，所以，平移后所得到的函數圖象對應的函數表達式就為y=2(x+1)2+4．

【評注】由于平移變換只改變函數圖象的位置而不改變其形狀(即不改變二次項系數)，所以只改變二次函數圖象的頂點位置(即只改變一次項和常數項)，所以，首先將二次函數的解析式變形為頂點式，然后，再依據平移變換后的二次函數圖象的頂點位置求出平移后函數圖象所對應的解析式．

【變式】

1.把二次函數y=-x2的圖象向左平移1個單位，然后向上平移3個單位，則平移后的圖象對應的二次函數的關系式為

( )

A．y=-(x-1)2-3 B．y=-(x+1)2-3

C．y=-(x-1)2+3 D．y=-(x+1)2+3

2.把拋物線y=-2x2向上平移1個單位，得到的拋物線是

( )

A．y=-2(x+1)2B．y=-2(x-1)2

C．y=-2x2+1 D．y=-2x2-1

6.4 對稱變換

【典例】求把二次函數y=2x2-4x+1的圖象關于下列直線對稱后所得到圖象對應的函數解析式：

(1)直線x=-1；

(2)直線y=1．

【解析】(1)由y=2x2-4x+1=2(x-1)2-1可知，函數y=2x2-4x+1圖象的頂點為A(1,-1)，所以，關于直線x=-1對稱后所得到圖象的頂點為A1(-3,-1)，所以，二次函數y=2x2-4x+1的圖象關于直線x=-1對稱后所得到圖象的函數解析式為y=2(x+3)2-1，即y=2x2+12x+17．

(2)由y=2x2-4x+1=2(x-1)2-1可知，函數y=2x2-4x+1圖象的頂點為A(1,-1)，所以，關于直線y=1對稱后所得到圖象的頂點為B(1,3)，且開口向下，所以，二次函數y=2x2-4x+1的圖象關于直線y=1對稱后所得到圖象的函數解析式為y=-2(x-1)2+3，即y=-2x2+4x+1．

【評注】在把二次函數的圖象關于與坐標軸平行的直線進行對稱變換時，具有這樣的特點——只改變函數圖象的位置或開口方向、不改變其形狀，因此，在研究二次函數圖象的對稱變換問題時，關鍵是要抓住二次函數的頂點位置和開口方向來解決問題．

【變式】求把二次函數y=x2-4x+1的圖象關于下列直線對稱后所得到圖象對應的函數解析式：

(1)直線x=-2；

(2)直線y=1．

高中數學基礎知識準備(代數部分)

1.數域的擴充

1.1數的分類

【變式】(1)(3)(4) 【解析】(1)正確.正整數如1,2,3，…，是正數也是實數；

(2)錯誤.自然數包含0,0不是正整數；

(3)正確.整數可以分為奇數和偶數,奇數包含±1,±3,±5，…，偶數包含0,±2,±4,±6,…；

(4)正確.質數是2,3,5,7,11,13，…，都是正整數；

(5)錯誤.無限不循環小數都是無理數，有限小數和無限循環小數都是有理數；

(6)錯誤.分數是有理數.

1.2二次根式

【變式】

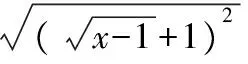
1.3有理化因式

【變式】

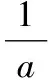
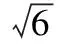
3.甲和乙

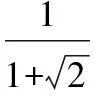
2.式子的運算

2.1合并同類項與通分

【變式1】

1.D 【解析】由x2+mx-10=(x+a)(x+b)可知ab=-10，從而x2+mx-10=(x+5)(x-2)或x2+mx-10=(x+2)(x-5)或x2+mx-10=(x+1)(x-10)或x2+mx-10=(x-1)(x+10),即x2+mx-10=x2+3x-10或x2+mx-10=x2-3x-10或x2+mx-10=x2-9x-10或x2+mx-10=x2+9x-10,因此m=±3或m=±9,故選D.

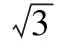
3.1×2×3×…×2 016,2 016,1 【解析】(x+1)(x+2)(x+3)·…·(x+2 016)的展開式中有2 016個x相乘，所以其多項式的次數是2 016；因為x的系數都是1，所以最高次項系數是1；常數項是1×2×3×…×2 016.

4.8 【解析】(1-i)(1+2i)2=(1-i)(4i-3)=1+7i=p+qi,所以p=1,q=7則p+q=8.

5.【解析】(1)原式=1-(4i)2=1-16i2=1+16=17.

(2)原式=9-12i+(2i)2=9-12i+4i2=9-12i-4=5-12i.

(3)原式=(1-4i)(1+4i)(7+2i)=17(7+2i)=119+34i.

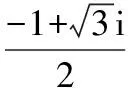
(5)(1+i)2=1+2i-1=2i，(1+i)8=24，所以(1+i)2017=[(1+i)8]252×(1+i)=21008(1+i).

【變式2】

2.2多項式恒等對應項系數相等

【變式】

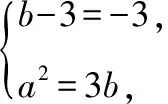
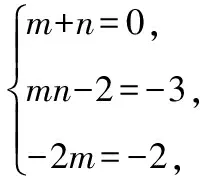
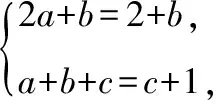
2.3利用恒等式將分式裂項

【變式】

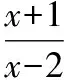
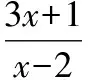
3.【證明】

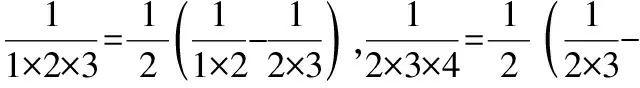
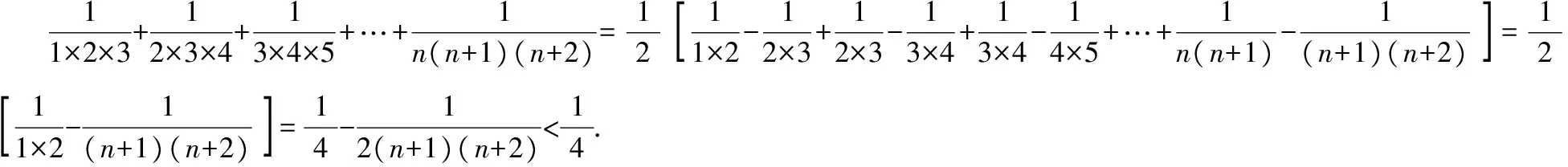
3.多項式乘法與分解因式

3.1立方和差公式

【變式】

1.【解析】(1)(3x-2y+1)(3x+2y-1)=[3x-(2y-1)][3x+(2y-1)]=(3x)2-(2y-1)2=9x2-(4y2-4y+1)=9x2-4y2+4y-1.

(2)(3a+2b+1)(3a-2b+1)=[(3a+1)+2b][(3a+1)-2b]=(3a+1)2-(2b)2=9a2+6a+1-4b2.

(3)(3x+y+1)(3x-y-1)=[3x+(y+1)][3x-(y+1)]=(3x)2-(y+1)2=9x2-y2-2y-1.

2.【解析】(1)原式=(3x)2+(2y)2+z2+2[3x·(-2y)+(-2y)z+(3x)z]=9x2+4y2+z2-12xy-4yz+6xz.

(2)原式=[(x-1)(x-4)][(x-2)(x-3)]=(x2-5x+4)(x2-5x+6)=(x2-5x)2+10(x2-5x)+24=x4-10x3+35x2-50x+24．

3.2完全立方和差公式

【變式】【解析】(1)(x-2y)3=x3+3x2(-2y)+3x(-2y)2+(-2y)3=x3-6x2y+12xy2-8y3．

(2)(x+2)4=[(x+2)2]2=(x2+4x+4)2=(x2)2+(4x)2+42+2x2×4x+2x2×4+2×4x×4=x4+8x3+24x2+32x+16．

3.3十字相乘法

【變式】

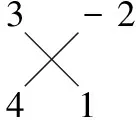
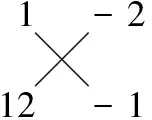
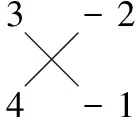
2.【解析】

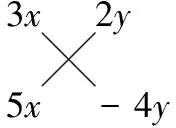
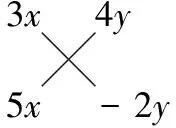
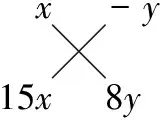
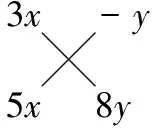
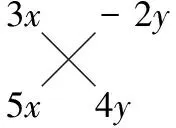
4.一元二次方程的根

4.1判別式

【變式】(1)該方程的根的判別式為Δ=a2-4×1×(a-1)=(a-2)2，

①當a=2時，Δ=0，所以方程有兩個相等的實數根x1=x2=1；

②當a≠2時，Δgt;0，所以方程有兩個不相等的實數根x1=1,x2=a-1．

(2)該方程的根的判別式為Δ=22-4×1×a=4(1-a)，

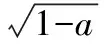
②當Δ=0，即a=1時，方程有兩個相等的實數根x1=x2=1；

③當Δlt;0，即agt;1時，方程沒有實數根．

4.2韋達定理

【變式】

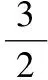
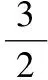
3.【解析】(法一)因為2是方程的一個根，

所以5×22+k×2-6=0，

所以k=-7．

所以方程為5x2-7x-6=0，

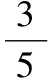
(法二)設方程的另一個根為x1，則

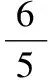
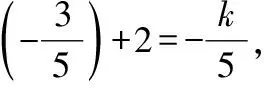
5.-2lt;blt;1 【解析】由條件得關于x的方程的判別式Δgt;0，即(a-1)2-4(ab-2)=a2-2(2b+1)a+9gt;0,此不等式的左邊是關于a的二次函數，要使函數值恒為正數，當且僅當4(2b+1)2-36lt;0，所以-2lt;blt;1.

5.方程組

5.1二元一次方程組

【變式】

1.【解析】(1)×2得6x+4y=10(3)，

(3)-(2)得0=4不成立，

所以方程組無解．

2.【解析】(1)×2得6x+4y=6(3)，

(3)-(2)得0=0恒成立，

所以方程組有無數組解．

5.2二元二次方程組

【變式】

1.【解析】由(1)得y=2x(3)，

將(3)代入(2)得x2-(2x)2+3=0，

解得x1=1或x2=-1．

把x=1代入(3)得y1=2；

把x=-1代入(3)得y2=-2．

2.【解析】由(2)得x=2y+2 (3),

把(3)代入(1),整理得8y2+8y=0，

解得y1=0,y2=-1．

把y1=0代入(3),得x1=2；

把y2=-1代入(3),得x2=0．

3．【解析】由(1)得y=-2x+2 (3),

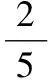
把x1=0代入(3)得y1=2；

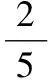
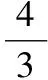
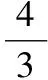
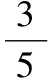
6.二次函數

6.1解析式的待定系數求法

【變式】

1.【解析】因為二次函數的最大值為2，而最大值一定是其頂點的縱坐標，

所以頂點的縱坐標為2．又頂點在直線y=x+1上，所以2=x+1，所以x=1．所以頂點坐標是(1,2)．設該二次函數的解析式為y=a(x-1)2+2(alt;0)，

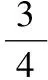
2.【解析】設該二次函數為y=ax2+bx+c(a≠0)

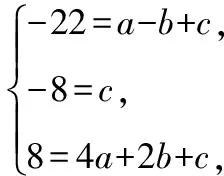
解得a=-2,b=12,c=-8．

所以所求的二次函數為y=-2x2+12x-8．

6.2最值與變化趨勢

【變式】

1.A 【解析】y=x2-4x-7配方得y=(x-2)2-11，該函數的最小值是-11，故選A.

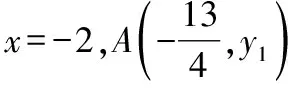
3.C 【解析】設二次函數y=(x-a)(x-b)，直線y=1，原方程的解即為兩圖象交點的橫坐標，由圖可知x1lt;alt;blt;x2，故選C.

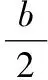
5.xgt;-3(或x≥-3) 【解析】拋物線開口向下，當xlt;-3時，y隨x的增大而增大；當xgt;-3時，y隨x的增大而減小.

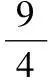
6.3平移變換

【變式】

1.D 【解析】函數y=-x2的頂點坐標為(0,0)，向左平移1個單位，然后向上平移3個單位后頂點坐標為(-1,3)，所以平移后的解析式為y=-(x+1)2+3，故選D.

2.C 【解析】原拋物線的頂點是原點，平移后頂點是(0,1)，得到的拋物線是y=-2x2+1，故選C.

6.4對稱變換

【變式】

1.【解析】(1)由y=x2-4x+1=(x-2)2-3可知，函數y=x2-4x+1圖象的頂點為A(2,-3)，所以，關于直線x=-2對稱后所得到圖象的頂點為A1(-6,-3)，所以，二次函數y=x2-4x+1的圖象關于直線x=-2對稱后所得到圖象的函數解析式為y=(x+6)2-3，即y=x2+12x+33．