新課標下的概率統計考點分析與命題規律

江蘇 宋衛東

新課標下的概率統計考點分析與命題規律

江蘇 宋衛東

新課標指出，中國學生在數學學習中應培養數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數據分析六大核心素養，它是每一名學生獲得成功生活、適應個人終生發展和社會發展都不可或缺的共同素養.在概率統計部分中，頻率分布直方圖是其中重要的考點，頻率分布直方圖作為一種提供背景材料的很好載體和工具，被稱為考查簡單數據處理能力的重要載體，因此備受高考命題者的青睞，仔細分析近年來，尤其是近幾年的高考試卷會發現，頻率分布直方圖、莖葉圖等圖表問題成為僅次于數學文化素養考查的熱點題型.

一、高考對頻率直方圖性質特征的考查

1. 頻率分布直方圖的縱坐標

【例1】(2016·山東理)某高校調查了200名學生每周的自習時間(單位：小時)，制成了如圖所示的頻率分布直方圖，其中自習時間的范圍是[17.5，30]，樣本數據分組為[17.5，20)， [20，22.5)， [22.5,25)，[25，27.5)，[27.5，30].根據直方圖，這200名學生中每周的自習時間不少于22.5小時的人數是

( )

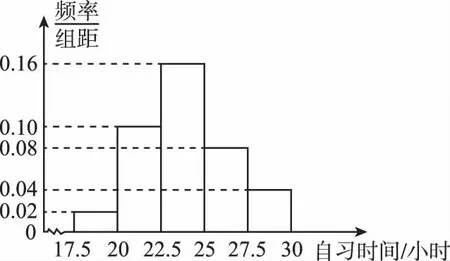
A.56 B.60 C.120 D.140

【解析】自習不少于22.5小時是后三組，200×(0.16+0.08+0.04)×2.5=140，故選D.

2.畫頻率分布直方圖

【例2】(2014·廣東理·第17題)隨機觀測生產某種零件的某工廠25名工人的日加工零件數(單位：件)，獲得數據如下：30，42，41，36，44，40，37，37，25，45，29，43，31，36，49，34，33，43，38，42，32，34，46，39，36，根據上述數據得到樣本的頻率分布表如下：

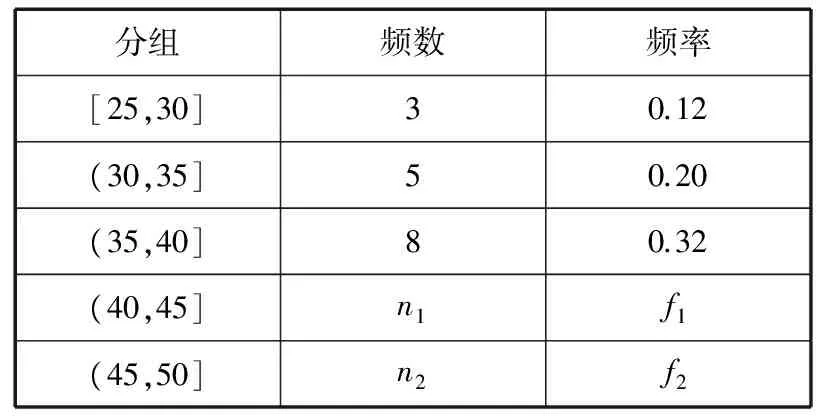
分組頻數頻率[25，30]30．12(30，35]50．20(35，40]80．32(40，45]n1f1(45，50]n2f2

(Ⅰ)確定樣本頻率分布表中n1,n2,f1和f2的值；

(Ⅱ)根據上述頻率分布表，畫出樣本頻率分布直方圖；

(Ⅲ)根據樣本頻率分布直方圖，求在該廠任取4人，至少有1人的日加工零件數落在區間(30,35]的概率.

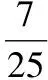
(Ⅱ)樣本頻率分布直方圖如下：

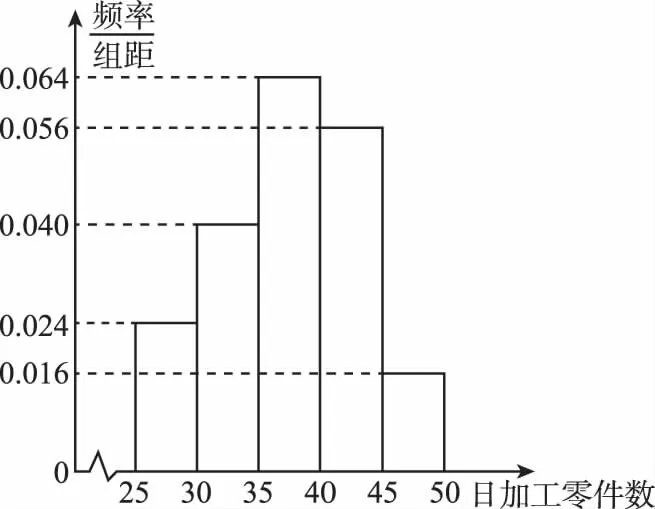
(Ⅲ)根據樣本頻率分布直方圖，每人的日加工零件數落在區間(30,35]的概率為0.2，

設所取的4人中，日加工零件數落在區間(30,35]的人數為ξ，則ξ～B(4,0.2)，

P(ξ≥1)=1-P(ξ=0)=1-(1-0.2)4=1-0.409 6=0.590 4，

所以4人中，至少有1人的日加工零件數落在區間(30,50]的概率約為0.590 4.

3.利用組中值代表區間內的數值

【例3】(2014·全國新課標Ⅰ理)從某企業生產的某種產品中抽取500件，測量這些產品的一項質量指標值，由測量結果得如下頻率分布直方圖：

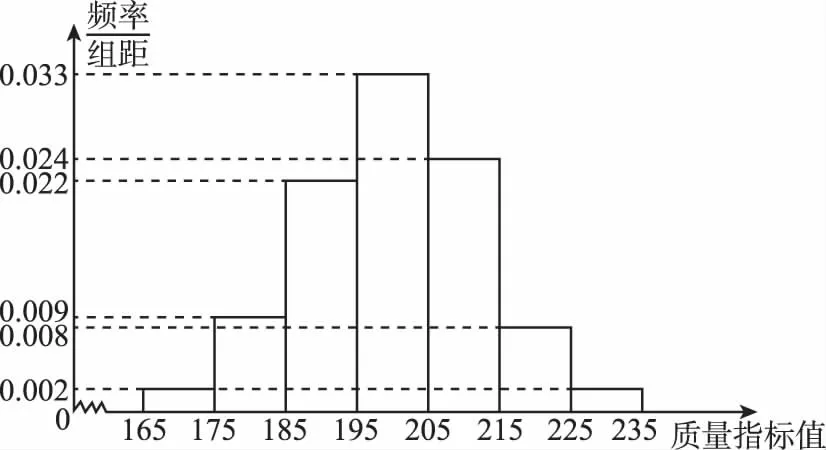
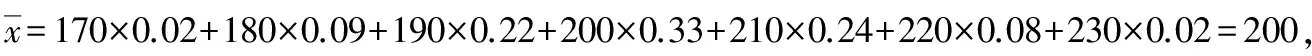
s2=(-30)2×0.02+(-20)2×0.09+(-10)2×0.22+0×0.33+102×0.24+202×0.08+302×0.02=150.

點評：組中值是上下限之間的中點數值，以代表各組標志值的一般水平.組中值并不是各組標志值的平均數，各組標志值的平均數在統計分組后很難計算出來，就常以組中值近似代替.由頻率分布直方圖可估計樣本特征數，如眾數、中位數、均值、方差.若同一組數據用該組區間中點代表，則眾數為最高矩形的中點橫坐標，中位數為左邊和右邊的小長方形的面積和是相等的點，均值為每個矩形的中點橫坐標與該矩形面積的累加值，方差是矩形的橫坐標與均值的差的平方的加權平均值.

4.柱狀圖與直方圖的區別

【例4】(2016·全國新課標Ⅰ理)某公司計劃購買2臺機器,該種機器使用三年后即被淘汰.機器有一易損零件,在購進機器時,可以額外購買這種零件作為備件,每個200元.在機器使用期間,如果備件不足再購買,則每個500元.現需決策在購買機器時應同時購買幾個易損零件,為此搜集并整理了100臺這種機器在三年使用期內更換的易損零件數,得下面柱狀圖：

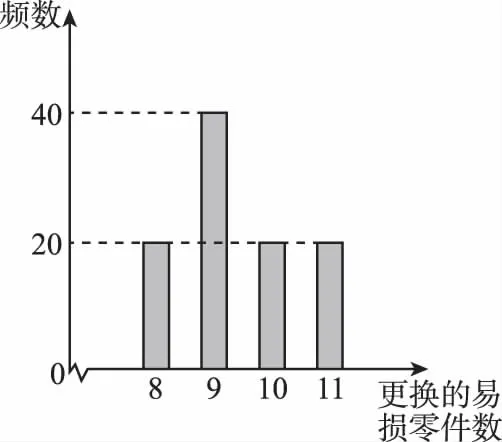
以這100臺機器更換的易損零件數的頻率代替1臺機器更換的易損零件數發生的概率，記X表示2臺機器三年內共需更換的易損零件數，n表示購買2臺機器的同時購買的易損零件數.

(Ⅰ)求X的分布列；

(Ⅱ)若要求P(X≤n)≥0.5，確定n的最小值.

【解析】(Ⅰ)先確定X取值分別為16,17,18,19,20,21,22,再用相互獨立事件概率模型求概率,然后寫出分布列：

X16171819202122P0．040．160．240．240．200．080．04

(Ⅱ)P(X≤18)=0.44，P(X≤19)=0.68，滿足P(X≤n)≥0.5的n的最小值是19.

點評：柱狀圖是一種以長方形的長度為變量的表達圖形的統計報告圖，由一系列高度不等的縱向條紋表示數據分布的情況，用來比較兩個或以上的價值(不同時間或者不同條件)，只有一個變量，通常用于較小的數據集分析.

二、高考對頻率直方圖在實際生活中的應用的考查

1.用樣本頻率分布估計總體頻數

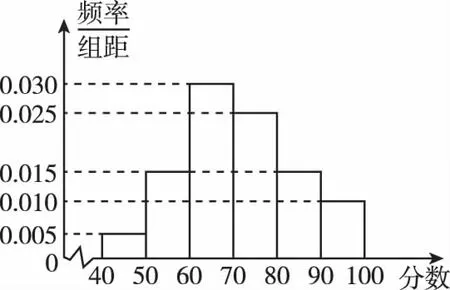
【例5】(2013·福建理)某校從高一年級學生中隨機抽取部分學生,將他們的模塊測試成績分成6組：[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以統計,得到如圖所示的頻率分布直方圖.已知高一年級共有學生600名,據此估計,該模塊測試成績不少于60分的學生人數為

( )

A.588 B.480

C.450 D.120

【解析】由頻率分布直方圖知40～60分的頻率為(0.005+0.015)×10=0.2,故估計不少于60分的學生人數為600×(1-0.2)=480.故選B.

點評：在頻率分布直方圖中，每個小矩形面積就是相應的頻率或概率，頻率×樣本容量=頻數，所有小矩形面積之和為1，這是解題的關鍵.

2.用樣本頻率估計概率

【例6】(2014·遼寧理)一家面包房根據以往某種面包的銷售記錄，繪制了日銷售量的頻率分布直方圖，如圖所示：

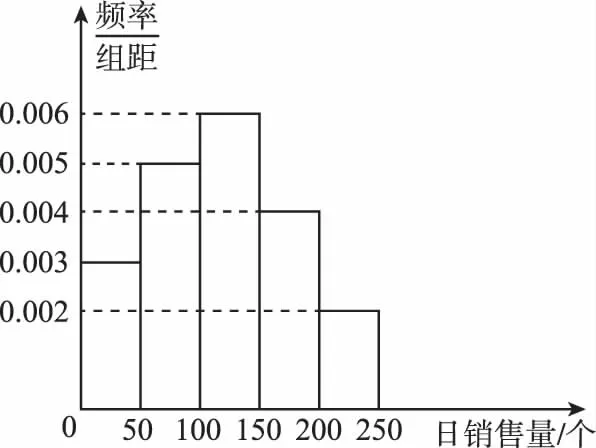
將日銷售量落入各組的頻率視為概率，并假設每天的銷售量相互獨立.

(Ⅰ)求在未來連續3天里，有連續2天的日銷售量都不低于100個且另一天的日銷售量低于50個的概率；

(Ⅱ)用X表示在未來3天里日銷售量不低于100個的天數，求隨機變量X的分布列、期望E(X)及方差D(X).

【解析】(Ⅰ)設A1表示事件“日銷售量不低于100個”，A2表示事件“日銷售量低于50個”，B表示事件“在未來連續3天里有連續2天日銷售量不低于100個且另一天的日銷售量低于50個”.因此可求出P(A1)=0.6，P(A2)=0.15，利用事件的獨立性即可求出P(B)=0.108.

(Ⅱ)由題意可知X～B(3,0.6),所以即可列出分布列，求出期望為E(X)和方差D(X)的值.因為X～B(3,0.6),所以期望為E(X)=3×0.6=1.8，方差D(X)=3×0.6×(1-0.6)=0.72.

點評：每個區間內的頻率就是本區間內所有個體個數與樣本容量的比值，這與古典概型概率計算原理是一致的，因此可以把頻率近似地看作概率.

3.用每組樣本頻率估計權重

【例7】(2016·北京文)某市民用水擬實行階梯水價，每人用水量中不超過w立方米的部分按4元/立方米收費，超出w立方米的部分按10元/立方米收費，從該市隨機調查了10 000位居民，獲得了他們某月的用水量數據，整理得到如下頻率分布直方圖：

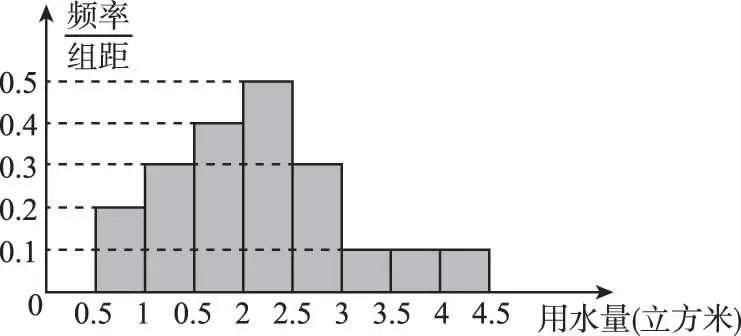
(Ⅰ)如果w為整數，那么根據此次調查，為使80%以上居民在該月的用水價格為4元/立方米，w至少定為多少？

(Ⅱ)假設同組中的每個數據用該組區間的右端點值代替，當w=3時，估計該市居民該月的人均水費.

【解析】(Ⅰ)由圖可知，用水量不超過2立方米的頻率是(0.2+0.3+0.4)×0.5=0.45，

用水量不超過3立方米的頻率是(0.2+0.3+0.4+0.5+0.3)×0.5=1.7×0.5=0.85.

顯然為使80%以上居民在該月的用水價格為4元/立方米，w至少定為3.

(Ⅱ)由用水量的頻率分布直方圖及題意，得居民該月用水費用的數據分組與頻率分布表：

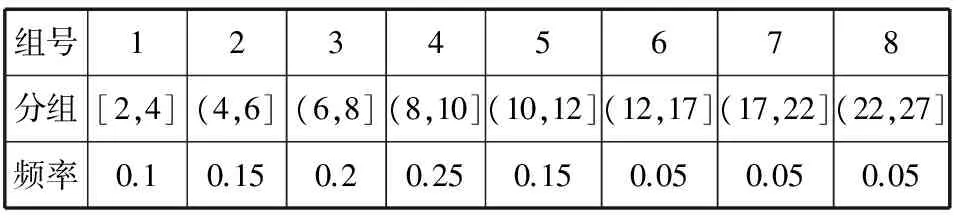
組號12345678分組[2，4](4，6](6，8](8，10](10，12](12，17](17，22](22，27]頻率0．10．150．20．250．150．050．050．05

根據題意，該市居民該月的人均水費估計為

4×0.1+6×0.15+8×0.2+10×0.25+12×0.15+17×0.05+22×0.05+27×0.05=10.5(元).

點評：頻率分布表在數量表示上比較準確，直方圖比較直觀，頻率分布表中的頻數之和等于樣本容量.居民該月的人均水費，也就是總水費除以樣本容量10 000，其中計算總水費可以一人一人地加起來，也可以對落在每個區間內的人數乘以相應的水費，再加起來，而后者再分別除以樣本容量之后，實際上頻率就成了每個水費數據的權重，這就是一種簡便計算.

4.用左右頻率的和相等的點估計中位數

【例8】(2016·四川文)我國是世界上嚴重缺水的國家，某市為了制定合理的節水方案，對居民用水情況進行了調查，通過抽樣，獲得了某年100位居民每人的月均用水量(單位：噸)，將數據按照[0,0.5)， [0.5,1)，…，[4,4.5]分成9組，制成了如圖所示的頻率分布直方圖.

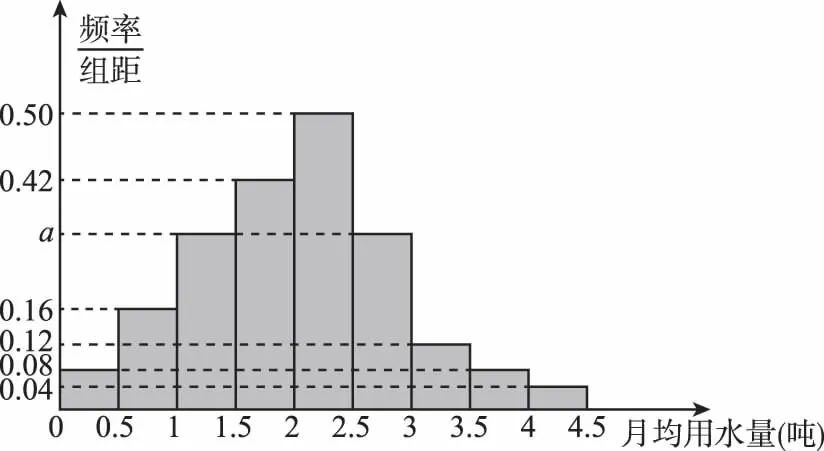
(Ⅰ)求直方圖中的a值；

(Ⅱ)設該市有30萬居民，估計全市居民中月均用水量不低于3噸的人數,說明理由；

(Ⅲ)估計居民月均用水量的中位數.

【解析】(Ⅰ)由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a，解得a=0.30.

(Ⅱ)100位居民月均用水量不低于3噸的頻率為0.06+0.04+0.02=0.12.

由以上樣本的頻率分布，可以估計30萬居民中月均用水量不低于3噸的人數為300 000×0.12=36 000.

(Ⅲ)設中位數為x噸.因為前5組的頻率之和為 0.04+0.08+0.15+0.21+0.25=0.73gt;0.5，

而前4組的頻率之和為0.04+0.08+0.15+0.21=0.48lt;0.5,

所以2≤xlt;2.5.由0.50×(x-2)=0.5-0.48，解得x=2.04.

故可估計居民月均用水量的中位數為2.04噸.

點評：在一般問題中，中位數就是將所有數據按照從小到大順序排列，位于最中間的數據或者相鄰兩個數據的均值，本題因為前5組的頻率之和為0.73gt;0.5，而前4組的頻率之和為0.48lt;0.5，所以中位數應該在第5組內，所以 2≤xlt;2.5，中位數x到2之間的頻率等于0.5(x-2)，也等于0.5-0.48，因此x=2.04.可見探求中位數的本質也是探究頻率恰為0.5時相應的用水量.

【變式】若該市政府希望使85%的居民每月的用水量不超過標準x(噸)，估計x的值，并說明理由.

【解析】因為前5組的頻率之和為0.04+0.08+0.15+0.21+0.25=0.73lt;0.85，

而前6組的頻率之和為0.73+0.30×0.5=0.88gt;0.85,

所以2.5≤xlt;3.由0.3×(x-2.5)=0.85-0.73，解得x=2.9.

所以，估計月用水量標準為2.9噸時，85%的居民每月的用水量不超過標準.

三、借助頻率直方圖高考對數理分析能力的考查

1.柱狀圖可以用分段函數表達

【例9】(2016·全國新課標Ⅰ文)某公司計劃購買1臺機器,該種機器使用三年后即被淘汰.機器有一易損零件,在購進機器時,可以額外購買這種零件作為備件,每個200元.在機器使用期間,如果備件不足再購買,則每個500元.現需決策在購買機器時應同時購買幾個易損零件,為此搜集并整理了100臺這種機器在三年使用期內更換的易損零件數,得下面柱狀圖：

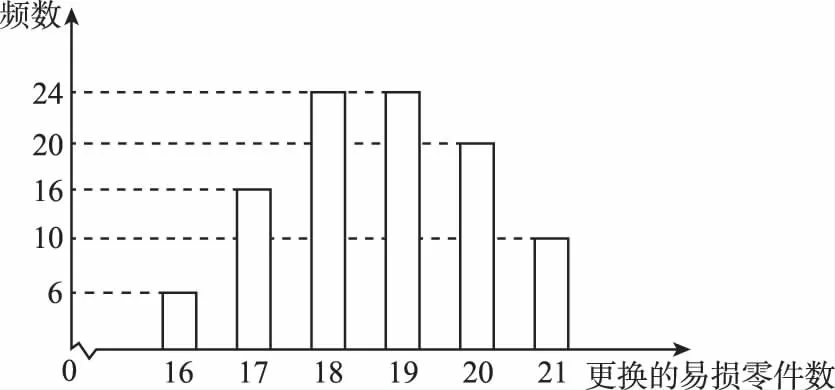
記x表示1臺機器在三年使用期內需更換的易損零件數,y表示1臺機器在購買易損零件上所需的費用(單位：元),n表示購機的同時購買的易損零件數.

(Ⅰ)若n=19,求y與x的函數解析式；

(Ⅱ)若要求“需更換的易損零件數不大于n”的頻率不小于0.5,求n的最小值；

(Ⅲ)假設這100臺機器在購機的同時每臺都購買19個易損零件,或每臺都購買20個易損零件,分別計算這100臺機器在購買易損零件上所需費用的平均數,以此作為決策依據,購買1臺機器的同時應購買19個還是20個易損零件？

【解析】(Ⅰ)因為購機的同時購買的易損零件數為19，

所以當x≤19時,y=3 800;

當xgt;19時，y=3 800+500(x-19)=500x-5 700.

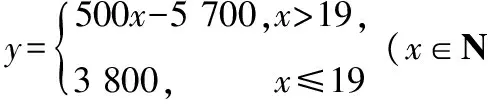
(Ⅱ)由柱狀圖知,需更換的零件數不大于18的概率為0.46,不大于19的概率為0.7,故n的最小值為19.

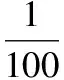
若每臺機器在購機同時都購買20個易損零件，則這100臺機器中有90臺在購買易損零件上的費用為4 000元，10臺的費用為4 500元.

比較兩個平均數可知,購買1臺機器的同時應購買19個易損零件.

點評：柱狀圖本身不連續，圖形只有高度沒有寬度，它的高就是頻數.柱狀圖在本題中起到了提供數據的作用，并且更為直觀形象.

2.頻率直方圖可用分段函數表達

【例10】(2013·全國新課標Ⅱ文·第19題)經銷商經銷某種農產品，在一個銷售季度內，每售出1 t該產品獲利潤500元，未售出的產品，每1 t虧損300元.根據歷史資料，得到銷售季度內市場需求量的頻率分布直方圖，如圖所示.經銷商為下一個銷售季度購進了130 t該農產品.以X(單位：t,100≤X≤150)表示下一個銷售季度內的市場需求量，T(單位：元)表示下一個銷售季度內經銷該農產品的利潤.

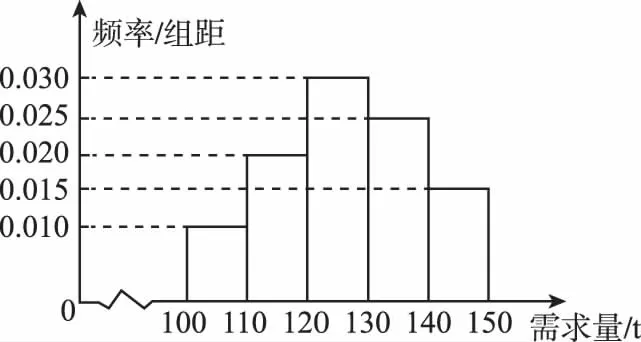
(Ⅰ)將T表示為X的函數；

(Ⅱ)根據直方圖估計利潤T不少于57 000元的概率.

【解析】(Ⅰ)當X∈[100,130)時，T=500X-300(130-X)=800X-39 000；

當X∈[130,150]時，T=500×130=65 000，

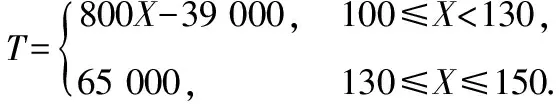
(Ⅱ)由(Ⅰ)知利潤T不少于57 000元當且僅當120≤X≤150.

由直方圖知需求量X∈[120,150]的頻率為0.7，所以下一個銷售季度內的利潤T不少于57 000元的概率的估計值為0.7.

點評：頻率分布直方圖所研究的數據是分區存放的，在該區內的數據都滿足同樣函數關系，因此頻率分布直方圖也可以用分段函數表達.此外頻率分布直方圖可以很好地反應數據分布規律服從正態分布，2014全國新課標Ⅰ理第18題就考查過該種問題.

江蘇省贛榆縣教育局教研室)