函數對稱性簡化多元函數積分問題研究

黃 永 ，李彥紅

（昭通學院 數學與統計學院， 云南 昭通 657000）

函數對稱性簡化多元函數積分問題研究

黃 永 ，李彥紅

（昭通學院 數學與統計學院， 云南 昭通 657000）

對稱性在數學及其更廣泛的領域有著重要的意義，在微積分計算中，對稱性有著重要的簡化運算作用.根據函數的對稱性對多元函數的積分問題作深入系統的討論.

對稱性；多元函數；重積分；曲線積分；曲面積分

引言

對稱性可簡化一元函數的定積分，同樣可以簡化多元函數的積分.多元函數積分包括重積分和線面積分，線面積分計算是轉化為重積分的計算，所以多元函數的積分問題最終是重積分的計算.本文將在文[2]基礎上進一步利用函數的對稱性與反對稱性對多元函數積分問題作系統探討.

函數的對稱性實質是其幾何圖形或幾何體的對稱性，它包括幾何圖形或幾何體關于點、關于直線及關于平面的對稱.一元函數關于點、直線的對稱性與反對稱性有以下常用關系：

對于多元函數也有類似的結論，但多元函數的這些對稱性情況較為復雜，這里主要就多元函數的一些特殊情形作討論.

1 預備知識

則稱 f(x,y)在D關于z軸對稱（原點反對稱）.

2 有關定理和推論

2.1 二重積分問題

定理1 若函數 f(x,y)在積分區(qū)域D關于平面x=0對稱（反對稱），則

即：

有

定理2 若函數 f(x,y)在積分區(qū)域D關于平面y=0對稱（反對稱），則

定理3 若函數 f(x,y)在積分區(qū)域D關于平面x=0與 y=0都對稱，則

推論1 若函數 f(x,y)在積分區(qū)域D關于平面x=a對稱（反對稱），則

推論4 若函數f(x,y)在積分區(qū)域D關于平面y=x 對稱，則

類似地，f(z,x)f(y,z)關于平行于坐標平面的平面、平行于坐標軸的直線及坐標平面上的點等對稱，也有相應的結論.

2.2 三重積分問題

2.3 曲線積分問題

對于定義在平面或空間曲線段上的函數，其對稱性同樣不便從幾何上解釋，但上述結論仍可得到推廣，有如下常用結論：

定理5 設函數f(x,y)在平面分段光滑曲線L連續(xù).若曲線關于x對稱，且則

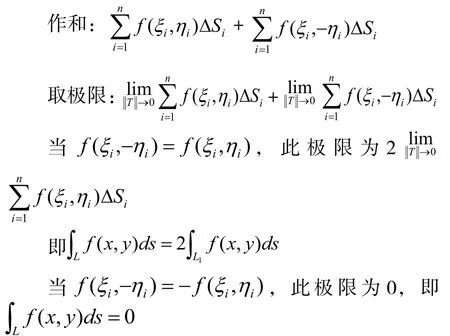
推論6 設函數f(x,y)在平面分段光滑曲線L連續(xù).若曲線關于x，y軸都對稱，則

2.4 曲面積分問題

其中S1為面一側的部分.

其中S1為第一卦限的部分.

3 函數的對稱性應注意的問題

3.1 函數的對稱性實質是其幾何圖形或幾何體的對稱性，二元函數的幾何圖像是三維空間中

3.2 由于第二型曲線（面）積分的積分曲線（面）是有向曲線(定側曲面)的, 因此它的值不僅與被積函數和積分曲線（面）的幾何形狀有關,還與積分曲面的側有關.在使用對稱性時, 除了考慮被積函數和積分曲線（面）的幾何形狀這兩方面的對稱性，還要考慮積分曲線（面）上的法線方向的指向情況.因此在計算第二型曲線（面）積分時，一般應在將第二型曲線（面）積分化為第一型曲線（面）積分或二重積分后，再考慮是否可利用對稱性來簡化其計算.

[1]華東師范大學數學系.數學分析[M].北京：高等教育出版社，2010.

[2]黃永，康道坤.對稱性性質簡化一類定積分計算問題研究[J].隴東學院學報，2011（4）：1-3.

[3]馮愛萍．多元函數的對稱性研究[J].西安科技大學學報，2007（3）：527-530.

[4]王憲杰．對稱區(qū)域上二重積分和三重積分的計算[J].牡丹江師范學院學報，2007（4）：65－66．

[5]劉渭川．利用對稱性計算曲線積分與曲面積分[J].河南科學，2006，24（6）：810－812．

[6]劉富貴．利用對稱性計算第二類曲線積分與曲面積分的方法[J].武漢理工大學學報，2006，12（6）：1069-1072．

[7]陳云新．輪換對稱性計算積分中的應用[J].高等數學研究，2001，4（1）：28－31．

Research on the Problem of Simplifying the Integration of Multiple Functions by Functional Symmetry

HUANG Yong, LI Yan-hong

(School of Mathematics and Statistics, Zhaotong University, Zhaotong 657000 China)

Symmetry is of important significance in mathematics and more extended region and it can simplify calculus calculation.In this paper we systematically explore of function of many variables Computing Problems by symmetry.

symmetry; function of many variables; multiple integrals; curve integral; surface integral

O172.2

A

2095-7408（2017）05-0009-03

2017-03-21

云南省教育廳科學研究基金資助項目 (2014Y499).

黃永（1966— ）女，云南昭通人，副教授，學士，主要從事基礎數學和數學教育研究.