圓錐曲線與直線相交的關聯問題*
——在章頭圖引領下對2017年全國高考Ⅰ卷（理）20題的探究

□翟洪亮

（江蘇省太湖高級中學，江蘇無錫214125）

圓錐曲線與直線相交的關聯問題*
——在章頭圖引領下對2017年全國高考Ⅰ卷（理）20題的探究

□翟洪亮

（江蘇省太湖高級中學，江蘇無錫214125）

圓錐曲線中的定點、定值問題是高考中的重點題型，有些圓錐曲線的高考試題看似平常，實質超常，往往蘊含漂亮的性質，有較大的研究空間和教學價值.由章頭圖知圓錐曲線都是由平面去截圓錐的截口而得，故在一種圓錐曲線中具有的性質通常可以類比到其他類型的圓錐曲線去.

圓錐曲線；斜率；定點；定值；類比；章頭圖

圓錐曲線中的定點、定值問題是高考中的重點題型，高考試題是經過命題專家組精心命制而成的，有些試題看似平常，實質超常，往往蘊含漂亮的性質，有較大的研究空間和教學價值，需要我們去挖掘．由圓錐曲線與方程的章頭圖可知，圓錐曲線是由平面去截圓錐的截口而得，故在一種圓錐曲線中具有的性質通常可以類比推廣到其他類型的圓錐曲線中去.在圓錐曲線與方程的章頭圖的引領下，現對2017年全國高考Ⅰ卷（理）中的一道解析幾何題進行探究，與大家進行交流．

一、試題呈現

（1）求C的方程；

（2）設直線l不經過P2點且與C相交于A，B兩點．若直線P2A與直線P2B的斜率之和為-1，證明：l過定點．

分析 作為一道高考試題，命題者獨具匠心，要求考生從所給四點中進行選擇，通過甄別，在對橢圓基本性質考查的同時，也進行對學生推理能力和運算能力的考查，試題短小精悍，給人留下清新飄逸的感覺，在解題時用點斜式直線方程求定值，首先要考慮斜率是否存在，具體解法如下.

參考解答（1）由于P3，P4兩點關于y軸對稱，故由題設知C經過P3，P4兩點.

程為+y=1.

（2）當直線l的斜率存在時，設其直線方程為y=kx+m(m≠1)，與橢圓C方程聯立得(1+4k2)x2+8kmx+4m2-4=0．

設 A(x1,y1)，B(x2,y2)，則即(2k+1)x1x2+(m-1)(x1+x2)=0，將 x1+x2=-代入得 m=-2k-1，此時 Δ=-64k，存在 k使Δ＞0成立．

所以l的方程為y=k(x-2)-1，過定點(2,-1)．

當直線l的斜率不存在時，設 A(s,t)，B(s,-t)，由直線P2A與直線P2B的斜率之和為-1，得=-1，解得 s=-2，此時l的方程為x=2，與橢圓C只有一個交點，不合題意，舍去．

綜上可得，直線l過定點(2,-1)．

二、探究過程

對于此題，給出多余條件，讓學生先排除再求解，這種命題風格自然想到2009年江蘇省高考第14題：設{an}是公比為q的等比數列，|q|＞1，令 bn=an+1（n=1,2,…），若數列{bn}有連續四項在集合{- 53,-23,19,37,82}中，則6q= __．兩者類似，如出一轍．直線P2A與直線P2B的斜率之和為-1，與直線l的斜率k的取值無關，故可以不考慮Δ＞0．此題條件簡單，結論不一般！別解如下.

解：（1）P1(1,1)，P2(0,1)只能有一點在橢圓C上，同理只能有一點在橢圓C上，所以P1(1,1)一定不在橢圓C上．由P2(0,1)在橢圓C上得b=1，由在橢圓C上得a=2，所以橢圓C的方程為

（2）設直線l過定點D(x0,y0).當直線l的斜率存在時，設 A(x1,y1)，B(x2,y2)，直線 l2的 方 程 為y-y0=k(x-x0)，代入+y=1 ，得(4k2+1)x2+8k(y0-kx0)x+4(y0-kx0)2-4=0．故x1+x2=

又因為kP2A+kP2B=即(2k+1)x1x2+(y0-kx0-1)(x1+x2)=0，即(x02-2x0)k2+2(y0-1-x0y0)k+(y02-1)=0．

因為直線P2A與直線P2B的斜率之和為-1，與直線l的斜率 k的取值無關，所以

當直線l的斜率不存在時，同參考答案（略）．

綜上可得，直線l過定點(2,-1)．

做完此題，筆者進行如下探究．

探究1若直線P2A與直線P2B的斜率之和為定值λ，直線l是否過定點？定值λ與定點的坐標之間存在什么關系？

解 設直線l過定點D(x0,y0)．當直線l的斜率存在時，設 A(x1,y1)，B(x2,y2)，直線l2的方程為y-y0=k(x-x0)，代入+y=1，得(4k2+1)x2+8k(y0-kx0)x+4(y0-kx0)2-4=0．故x1+x2=又因為kP2A+kP2B=即(2k-λ)x1x2+(y0-kx0-1)(x1+x2)=0，整理得(-λx2-2x)k2+(2y+2λxy-2)k+(λ-λy2)000000=0．

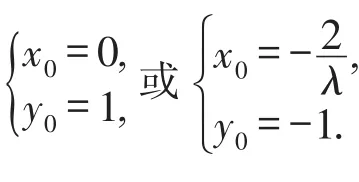
因為直線P2A與P2B的斜率之和為定值λ，與k的取值無關，故解得又直線l不經過P2點，所以直線l過定點(-,-1)．當直線l的斜率不存在時，設 A(s,t)，B(s,-t)，由已斜率之和為定值 λ，得得 s=-，當 -2＜-＜2時，即當λ＜-1或λ＞1時，直線l的方程為x=-，也過定點 (-,-1)．否則-1≤λ＜0 或0＜λ≤1，直線l與橢圓C不存在兩個交點，不合題意，舍去．

由上可知，定點是在定直線y=-1上，直線P2A與直線P2B的斜率之和為定值λ是隨著定點D(x0,y0)的橫坐標的數值的變化而改變的，且定值λ=-．

結論1若直線P2A與直線P2B的斜率之和為定值λ（λ≠0），則直線l經過定直線y=-1上的定點(x,-1)，且λ=-．

能否將上述性質推廣到一般情況？

證明：設直線l過定點D(x0,y0)．當直線l的斜率存在時，設 A(x1,y1)，B(x2,y2)，直線l的方程為 y-y0=k(x-x0)，代入b2x2+a2y2-a2b2=0，得 (a2k2+b2)x2+2a2k(y0-kx0)x+a2(y0-kx0)2-a2b2=0.故x1+x2=

因為直線PA與直線PB的斜率之和為λ，所以上式成立與k的取值無關，所以解得或又直線l不經過P點，所以直線l過定點

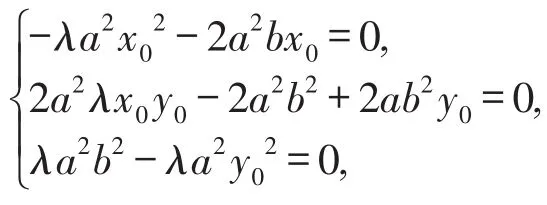
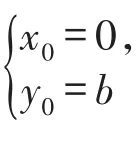
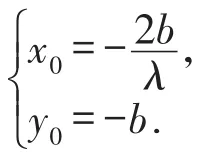
當直線l的斜率不存在時，設 A(s,t)，B(s,-t)，由已知斜率之和為定值 λ，得得當時，即當或時，l的方程為x=-，也過定點(-,-b)．否則 -≤λ＜0或0＜λ≤，直線l與橢圓C不存在兩個交點，不合題意，舍去．

由于點P(0,b)是橢圓的上頂點，位置特殊，因此自然地聯想到其他頂點時的情況，通過探究，同樣可得：

（1）若點 P(0,-b)，則直線l經過定直線y=b上的點D(x0,b)，且

（2）若點 P(a,0)，則直線l經過定直線x=a上的定點D(a,y0)，且

（3）若點P(-a,0)，則直線l經過定直線x=-a上的定點D(-a,y0)，且

由圓錐曲線與方程的章頭圖和章頭語可知，用一個垂直于圓錐的軸的平面去截圓錐，截口曲線是一個圓；用一個不垂直于圓錐的軸的平面去截圓錐，當截面與圓錐的軸夾角不同時，可以得到不同的截口曲線，它們分別是橢圓、雙曲線、拋物線，我們通常把圓、橢圓、雙曲線、拋物線統稱為圓錐曲線．既然圓、橢圓、雙曲線、拋物線都是由圓錐被平面所截，那么它們往往也具有類似的性質．橢圓中的上述性質在圓、雙曲線、拋物線中是怎樣的呢？

限于篇幅原因，以下探究過程省略．在圓C:x2+y2=r2中，通過探究可得如下結論：

結論4已知圓C:x2+y2=r2，設直線l不經過點P，且與C相交于A，B兩點．若直線PA與直線PB的斜率之和為定值λ（λ≠0）．

（1）若點 P(0,r)，則直線l經過定直線y=-r上的定點D(x0,-r)，且

（2）若點P(0,-r)，則直線l經過定直線y=r上的定點D(x0,r)，且

（3）若點 P(r,0)，則直線 l經過定直線x=r上的定點D(r,y0)，且

（4）若點 P(-r,0)，則直線l經過定直線x=-r上的定點D(-r,y0)，且

（1）若點 P(a,0)，則直線l經過定直線x=a上的定點D(a,y0)，且

（2）若點 P(-a,0)，則直線 l過定直線x=-a上的點(-a,y0)，且

在拋物線y2=2px (p＞0)中通過探究，可得如下結論：

結論6已知拋物線y2=2px (p＞0)的頂點為P，設直線l與C相交于A，B兩點．若直線OA與直線OB的斜率之和為定值λ（λ≠0），則直線l經過定直線x=0上的定點D(0,y0)，且

*本文系江蘇省教育科學“十三五”規劃課題“對高中數學教科書中章頭圖和章頭語的教學研究”〔課題編號：B-b/2016/02/118〕的研究成果.