高中物理教學要關注學生的“三個點”

□陳報南

（浙江師范大學附屬中學，浙江金華321004）

高中物理教學要關注學生的“三個點”

□陳報南

（浙江師范大學附屬中學，浙江金華321004）

高中物理教學要關注學生的“三個點”——“興趣點”、“困惑點”和“隱性點”，這是發展學生核心素養的一種有效方法.關注“興趣點”的策略是利用實驗、物理學史、物理學悖論來激發學生的“興趣點”.關注“困惑點”的策略是從“興趣點”中提煉出“困惑點”、在科學探究中增添“困惑點”.關注“隱性點”的策略是暴露學生錯誤的“隱性點”、點破學生視而未見的“隱性點”.

核心素養；物理教學；興趣點；困惑點；隱性點

物理核心素養的培養是本次基礎教育課程改革的根本目標.如何讓物理核心素養落地，是廣大高中物理教師都在思考的問題.在實踐中，我們發現，高中物理教學要關注學生的“三個點”，即“興趣點”、“困惑點”和“隱性點”.這是發展學生物理核心素養的一種有效策略.選擇這“三個點”的理由是：關注學生學習的“興趣點”，目的是激發學生的科學思維；關注學生學習的“困惑點”，目的是破解學生的疑問；關注學生學習的“隱性點”，目的是暴露隱藏在學生內心深處的錯誤觀念，點破學生沒有看到的隱蔽之處.

一、關注學生的“興趣點”

所謂興趣是最好的老師.教育學、心理學的研究均表明：只有學生感興趣的東西，他才樂學；只有樂學，才能掌握學習的主動性，才能克服困難把它學好.學生如果對物理學習產生了興趣，就會充分發揮自己的積極性和主動性，變得想學習、愛學習、會學習.因此，要發展學生的物理核心素養，首要一點在于激發學生學習物理的興趣點.“興趣點”是學生進行科學思維的起點，需要教師激發.關注學生的“興趣點”，主要有三種策略.

（一）用新奇的實驗產生“興趣點”

新奇的物理實驗能產生物理學習的“興趣點”，能激發學生的物理學習興趣，引發學生進一步探索的欲望.例如，在機械能守恒定律的教學中，用一根長繩懸掛一個鉛球來演示.教師背靠墻壁站著不動，一位學生將鉛球拉開較大的角度使之貼近教師的鼻子.學生放手后，鉛球擺動起來.很多學生都感到擔心，生怕擺回來的鉛球會砸破教師的鼻子.結果，教師安然無恙.學生感到非常驚訝.驚險的實驗，引發了學生學習的“興趣點”——擺回的鉛球為什么不會撞破教師的鼻子？為下一步科學探究做好了準備.

（二）用有趣的物理學史引發“興趣點”

物理學史中有很多有趣的事實，如經教師挖掘、運用，能有效引發學生物理學習的“興趣點”.例如，在能量守恒定律的學習中，教師介紹1914年的“能量失竊案”.當時，查德威克在做放射性實驗，結果發現一個有趣的現象.原子核A放射出β粒子后，變成原子核B，原子核B與β粒子的總能量卻比變化前原子核A的總能量要小.能量哪里去了，是被誰偷走了嗎？對此，有人認為，在微觀領域里，能量不再守恒；也有人認為，不管是宏觀世界還是微觀世界，只要有能量轉化，就一定遵守能量守恒定律.能量守恒定律是否普遍適用，真實的情況到底是怎樣的？簡明有趣的物理學史，激起了學生一探究竟的欲望.

（三）用物理學悖論激發“興趣點”

有些物理問題如果直白地說明，教學就會顯得死板.如果教師設置一些含有物理悖論的情境，學生通過理論推導發現其矛盾之處，效果就明顯不同.它能充分激發學生學習物理的興趣點.

案例：光的全反射教學

設置情境：已知玻璃的折射率為1.5，光從玻璃斜射入空氣中，入射角為60°，求折射角的大小.

設置理由：學生有一個前概念，認為光的折射定律是普遍適用的，如果已知折射率和入射角大小，就能根據光的折射定律求出折射角的大小.通過這一問題情境的求解，引發悖論，產生認知上的沖突，通過理論分析、實驗驗證，從而順利建立光的全反射概念.

12≈1.30＞1，發現與實際情況相矛盾.到底是什么原因造成sinθ1＞1的？是光的折射定律錯了嗎，好像又不是.

二、關注學生的“困惑點”

物理教學中，興趣點的激發只是一個引子，關鍵還需解決學生物理學習的困惑點.學生所糾結和困惑的問題，都是學習中的“困惑點”，每一個“困惑點”的突破都意味著科學思維的發展.

（一）從“興趣點”中提煉出“困惑點”

還以上述光的全反射教學為例.在興趣點激發之后，接下來的工作就是確定困惑點.如以“光的折射定律還能用嗎”為“困惑點”.然后對困惑點進行理論分析與實驗驗證.引導學生從理論上進行分析.①由得sinθ1＞sinθ2，θ1＞θ2，即光從玻璃斜射入空氣中時，折射角θ1大于入射角θ2.②光從玻璃斜射入空氣中時，由n 為一定值，可知：如入射角θ2增大，則折射角θ1也跟著增大.③當入射角 θ2增大到某一值（小于60°）時，折射角就已達到90°.再用實驗來驗證.利用激光演示儀，讓激光射到半圓形玻璃磚上，使光從玻璃射入空氣中的入射角由小增大，發現入射角增大到某一小于60°的角度時，折射光線剛好消失.入射角為60°時，已無折射光線，因此光的折射定律是正確的，只不過沒有了折射光線，求解折射角大小也就失去了意義.原有問題只是一個假問題而已.

（二）在科學探究中增添“困惑點”

人類對物理概念、物理規律的認識過程并非是一帆風順的，而是曲曲折折的.在物理教學中，需要設置情境，讓學生經歷人類認識物理概念、規律的“困惑點”.目的是發展學生的科學探究能力、科學思維和科學態度.

案例：光的折射定律的發現.

實驗演示：光從空氣斜射入玻璃，測出小角度范圍內的入射角與折射角如表1所示.然后讓學生尋找小角度入射角（5°～30°）與折射角的關系，學生自然想到直接找兩者的比值關系.發現的值接近1.53.看來，光從空氣斜射入玻璃時，折射角與入射角成正比關系.繼續增大入射角，記錄入射角（40°～80°）所對應的折射角大小，求出的值.學生發現在入射角較大時的值不再與入射角較小時的值相近.說明，光從空氣斜射入玻璃，入射角較大時，折射角與入射角不再成正比關系.與學生原先的學習經驗發生了矛盾.這就是教師在教學中設置的一個“困惑點”.

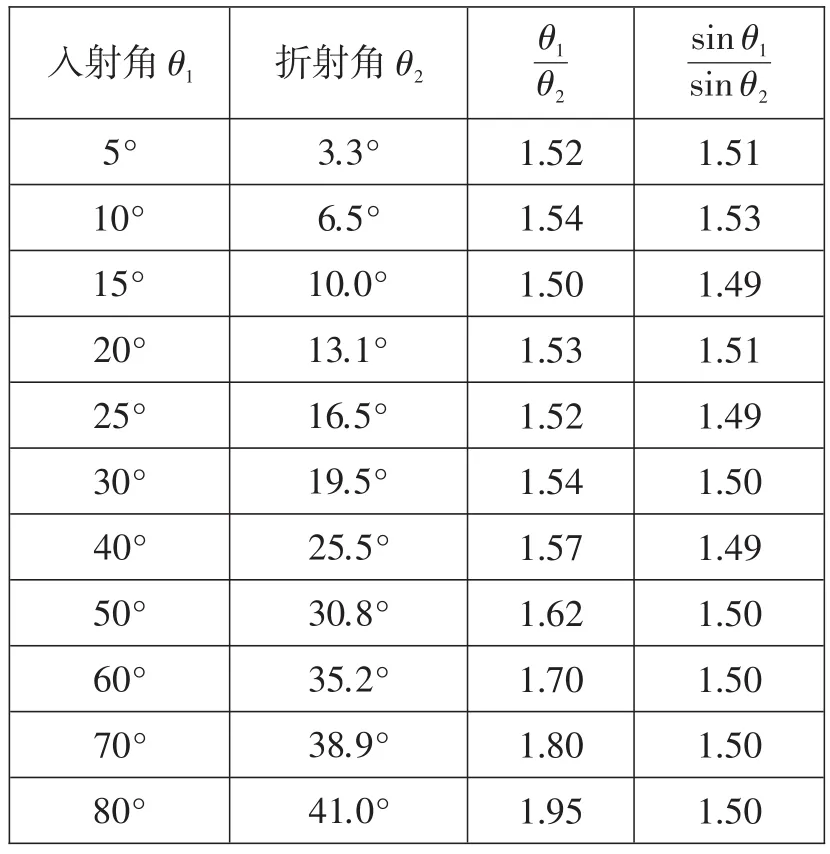
表1 尋找入射角與折射角的關系

教師引導學生跳出簡單的比值方法，采用其他數學方法如求三角函數值再相比的方法來尋找光的折射規律.學生通過計算，發現的值在入射角較小、較大時都是一個定值.說明，光從空氣斜射入玻璃時，入射角的正弦值與折射角的正弦值成正比關系.

學生的科學思維，就在感受困惑點、突破困惑點中得到發展.這樣的經歷是非常寶貴的，它是學生發展物理素養不可或缺的重要途徑.

三、關注學生的“隱性點”

關注學生的“隱性點”包括兩個方面，一是關注學生心中隱藏的錯誤觀點；二是關注學生沒有看到的隱蔽之處.暴露學生內心隱藏的錯誤觀點，才能使教學做到對癥下藥.點破學生沒有看到的隱蔽之處，才能使學生學到的東西能夠融會貫通，自成一體.關注學生“隱性點”的具體策略主要有兩個.

（一）挖掘錯誤的“隱性點”

學生的錯誤觀念常常隱藏在他們的內心深處.教師在教學中，需要關注學生錯誤的“隱性點”.教師設置情境，鼓勵學生提出問題，目的是暴露學生的“隱性問題”.

例如，電容概念“隱性點”的挖掘.

情境：教師出示超級電容器的圖片，如圖1所示.

圖1

提問1：從這個圖片上，你能獲得哪些信息？

學生容易說出：2.7V，3000F，電容器有正、負極.

提問2：有了這些信息，你能得出哪些相關的結論？

學生可能會說出：①電容器的額定電壓是2.7V；②電容器的擊穿電壓是2.7V；③電容器的電容是3000F；④電容器充滿電時，電容器所帶的電荷量是8.1×103C；⑤電容器充電時，左端與電源的正極相接，右端與電源的負極相接，不能接錯.根據說法①、②，教師需要組織學生討論電容器上所標電壓值的含義.

提問3：根據這些信息，你還能提出哪些問題？

有學生提出：電容器兩端的電壓是2.7V時，電容器的電容是3000F.這一問題暴露了很多學生心中的想法，需要進一步討論.教師可以追問：電容器不帶電時，電容器的電容是多少？然后組織學生討論電容大小的決定因素.

通過這種借助物理情境，組織學生討論開放性的物理問題，能很好地暴露學生概念學習中的“隱性”錯誤，鞏固學生所學的概念、規律.學生在“獲取信息——辨析疑難——提出問題——討論總結”中，發展了科學思維，形成了物理觀念.

（二）點破無視的“隱性點”

由于思維定勢的影響，大多數學生對一些物理問題會熟視無睹，看不到這些物理問題中隱藏的本質內容.這時，需教師點破他們所無視的“隱性點”.

案例：重力做功規律的教學，如圖2所示.

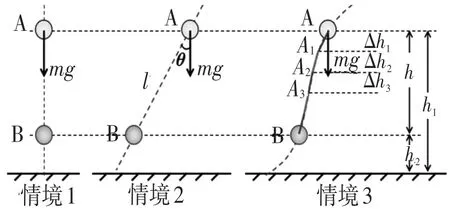
圖2

情境1：小球從A點沿豎直方向下落到B點，下落高度為h，求重力所做的功.

情境2：小球從A點沿傾斜直線向下運動到B點，下落高度為h，求重力所做的功.

情境3：小球從A點沿曲線路徑向下運動到B點，下落高度為h，求重力所做的功.

對于情境1：學生認為，重力方向與位移方向一致，重力做功為WG=mgh.

對于情境2：學生認為，重力方向與位移方向夾角為θ，重力做功為WG=mglcosθ=mgh.

對于情境3：大部分學生都提出用微元法，將曲線分割成很多段微小的直線段，每一小段中重力做功等同于情境2中的情況，做功為ΔWG=mgΔh，則全過程中重力 做 功為 WG=mgΔh1+mgΔh2+mgΔh3+…即WG=mgh.

教師表示肯定的態度.但學生沒有看到一個更為本質的問題：實際上，由于重力是恒力的緣故，在上述三種情境中，均可以用恒力做功的方法來求解.重力所做的功都等于重力與重力方向上位移大小的乘積.因此，教師做進一步的提問：對于情境3中重力做功的問題，還有更簡潔的求解方法嗎？能否從更為一般的角度來求解.

個別學生提出：由于重力是一個恒力，物體從A點到B點的過程中，物體沿重力方向通過的位移是h，根據恒力做功特點可以推知，重力所做的功就是重力與重力方向上位移大小的乘積，即WG=mgh.

教師給予充分的肯定，繼續點破：從上述三種情境中看，我們可以發現重力做功有什么特點？

至此，學生能夠說出，重力做功與路徑無關，而取決于物體的始末位置.

四、結語

總之，在高中物理教學中，教師要關注學生的“三個點”，即關注學生的“興趣點”、關注學生的“困惑點”和關注學生的“隱性點”.值得注意的是：第一，它的提出并非空穴來風，而是立足于“以學習者為中心”教學觀基礎上所提出的教學策略；第二，實踐表明，能有效地提升學生的物理核心素養；第三，發展學生的物理素養，要從關注學生的學習過程開始，關注學生的學習有多種答案，本文所說的僅是其中一種比較理想的答案.