例談幾何輔助線的添加規(guī)律

□高建成

（杭州市余杭教育學(xué)院，浙江杭州311100）

例談幾何輔助線的添加規(guī)律

□高建成

（杭州市余杭教育學(xué)院，浙江杭州311100）

在幾何解題教學(xué)中，為了證明結(jié)論的正確性，常常需要添加輔助線.輔助線的添加是有規(guī)律的.在教學(xué)中，教師應(yīng)該引導(dǎo)學(xué)生對幾何問題進(jìn)行逐步分析，隨著分析的進(jìn)程，輔助線就自然生成，結(jié)論的證明也就順理成章.

解題教學(xué)；基本圖形；輔助線；規(guī)律

在幾何教學(xué)中，學(xué)生常常會向教師提出這樣的問題：“老師，這條輔助線是怎樣想出來的？”“老師，添輔助線有規(guī)律嗎？”“添輔助線的規(guī)律是什么？”“老師，為什么你會想到這樣添輔助線，而我就想不到？”……要很好地回答學(xué)生的問題，教師就要回到幾何的本原，回歸基本圖形進(jìn)行思考與挖掘，前者是基于《幾何原本》邏輯推理的理性，這個思維鏈條太長；后者回歸基本圖形，是思維的濃縮與凝煉，能夠提高思維效率.

我們都知道，任何復(fù)雜的幾何圖形都是由基本圖形組成的，這些基本圖形是組成一個幾何問題圖形的最簡單、最重要、最基本的，但又是具有特定性質(zhì)的圖形，能明確地闡明應(yīng)用條件和應(yīng)用方法的圖形[1].添加輔助線利用基本圖形分析，就是一種建立在對每一個基本圖形和圖形性質(zhì)的分析、認(rèn)識、應(yīng)用基礎(chǔ)上，將不完整的、殘缺的基本圖形補(bǔ)充完整，從而添加輔助線的分析、思考方法.

任何一個復(fù)雜的平面幾何圖形，都是由若干個基本的平面幾何圖形組合而成，當(dāng)若干個基本的平面幾何圖形組合而成為一個平面幾何問題時，許多條件、性質(zhì)、結(jié)論就隱去了.所以幾何解題教學(xué)中的分析和思考，就是要將這一綜合過程反過來進(jìn)行，剖析、再現(xiàn)并找到這些基本的平面幾何圖形，應(yīng)用這些基本平面幾何圖形的條件、性質(zhì)、結(jié)論，使問題得到解決.

顯然，基本圖形不是構(gòu)成幾何圖形的基本元，例如線段、垂線、三角形、圓等，它們必須是完整的圖形，有特定的性質(zhì)，更為重要的是要能講清楚這個圖形的應(yīng)用條件和應(yīng)用方法，才能進(jìn)入基本圖形的集合.下面，以一道幾何證明題為例，說明如何利用基本圖形尋找、添加輔助線進(jìn)行解題教學(xué).

一、案例分析

案例：如圖1，已知在△ABC中，AB=AC，AD⊥BC，垂足是D，BE是∠ABC的角平分線，過E作EF⊥BE交BC于點(diǎn)F，EG⊥BC，垂足是G，求證：DG=BF.

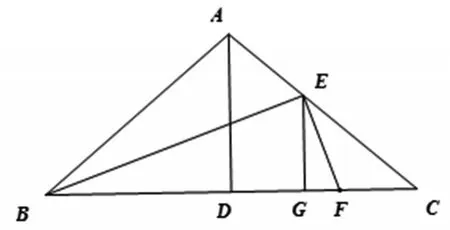
圖1

分析：本題的條件中出現(xiàn)BE是∠ABC的角平分線和EF⊥BE，EF既是角平分線又是BE的垂線，就出現(xiàn)角平分線和向角平分線所作的垂線，所以可應(yīng)用等腰三角形中重要線段的基本圖形進(jìn)行證明，角分垂，輔助線就呼之欲出.而現(xiàn)在角平分線BE的垂線EF與角的一邊BC已經(jīng)相交，而與另一邊BA尚未相交，所以應(yīng)將它們延長到相交，也就是延長FE交BA的延長線于點(diǎn)H，補(bǔ)全基本圖形（如圖2），這是基本圖形分析法中作輔助線的基本想法.

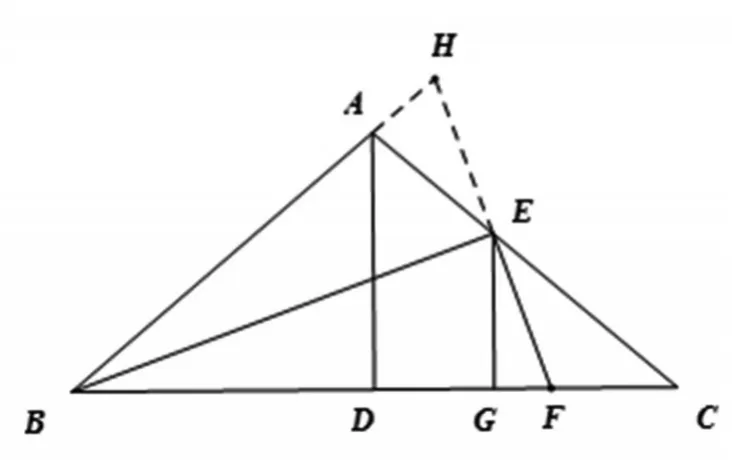
圖2

就可得△BEH≌△BEF，BH=BF，EH=EF，這里應(yīng)用的等腰三角形中的重要線段就是這個問題的第一個基本圖形（如圖3）.

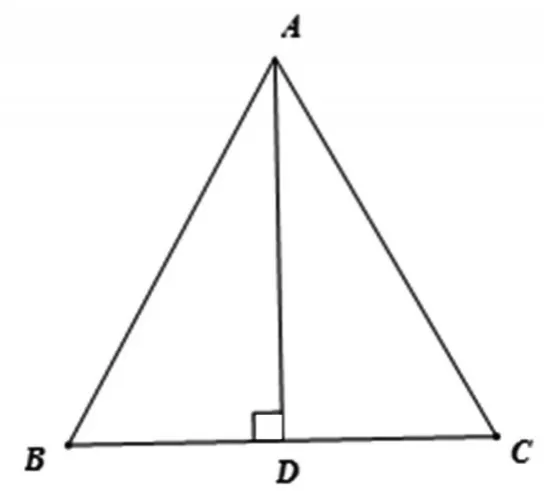
圖3

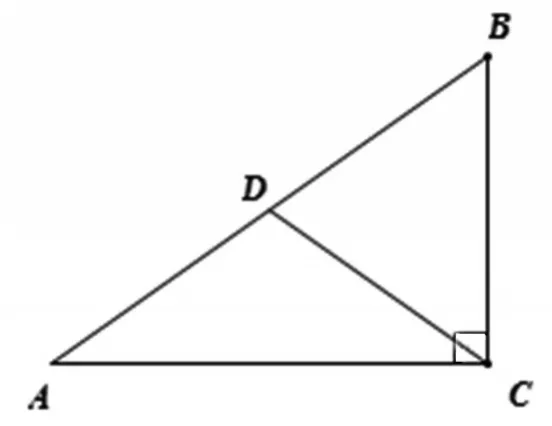
圖4

現(xiàn)在圖形中是有直角三角形而沒有斜邊上的中線，所以應(yīng)將斜邊上的中線添上，圖形上已有中點(diǎn)E，顯然就要取BH的中點(diǎn)I，連結(jié)EI交AD于點(diǎn)J，就可得EI=BH，這里應(yīng)用的直角三角形斜邊上的中線就是這個問題的第二個基本圖形，也就是添加第二條輔助線的來源（如圖5）.

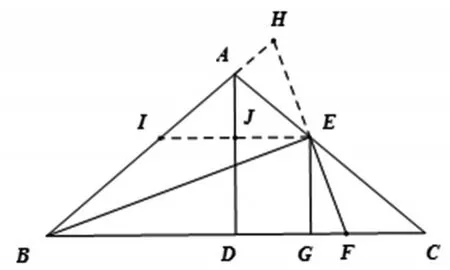
圖5

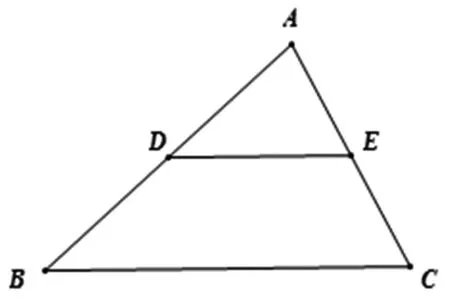
圖6

在證明了IE∥BF后，就出現(xiàn)IE是△ABC內(nèi)一條邊BC的平行線段，所以可應(yīng)用平行線型相似三角形進(jìn)行證明，也就可得△AIE∽△ABC，而已知AB=AC，AD⊥BC，垂足是D，所以AI=AE，AJ⊥IE，垂足是J，并可得J是IE的中點(diǎn)，JE=IE（如圖7）.

圖7

這里應(yīng)用的平行線型相似三角形就是這個問題的第四個基本圖形（如圖8）.

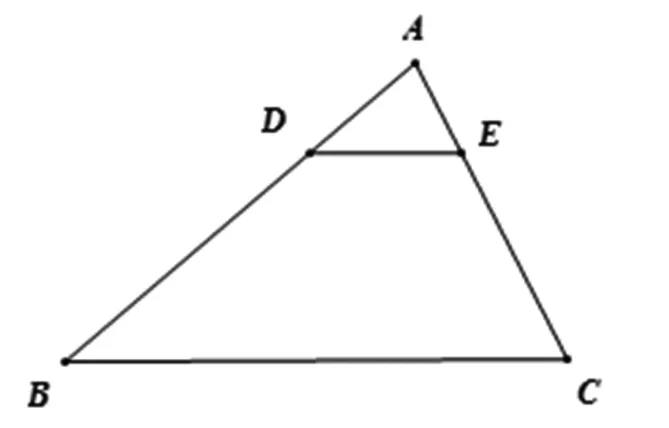
圖8

現(xiàn)在的問題就成為要證明DG=JE，由于條件還給出EG⊥BC，垂足是G，所以EG∥JD，而EJ∥GD，從而應(yīng)用平行線的性質(zhì)就能證明DG=JE，至此證明完成.這里應(yīng)用的平行線就是這個問題的第五個基本圖形（如圖9）.

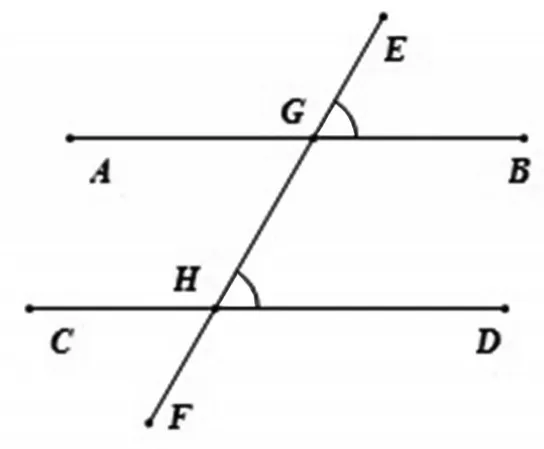
圖9

通過這一例題的分析，就可以發(fā)現(xiàn)像這樣一道比較復(fù)雜的幾何問題（圖形），實(shí)際上是由五個基本圖形組合而成的，分析并找到這五個基本圖形，也就找到了添加輔助線的位置，再應(yīng)用這五個基本圖形的性質(zhì)，就可以使問題得到解決，這樣一種分析方法就是基本圖形分析法，利用基本圖形分析來添加輔助線就找到了規(guī)律.

二、教學(xué)啟示

（一）幾何問題中輔助線的添加是有規(guī)律可循的

任何一個復(fù)雜的平面幾何圖形，都是由若干個基本的平面幾何圖形組合而成的，當(dāng)若干個基本的平面幾何圖形組合而成為一個平面幾何問題時，許多平面幾何圖形的條件、性質(zhì)、結(jié)論就隱去了，尋找基本的平面幾何圖形，并對殘缺、不完美的基本平面幾何圖形進(jìn)行補(bǔ)充和完善，就是添加輔助線的本質(zhì)、規(guī)律所在.對平面幾何圖形進(jìn)行剖析后發(fā)現(xiàn)，平面幾何中的基本圖形，綜合起來有七大類：全等三角形、相似三角形、等腰三角形、平行線、特殊角三角形、與面積方法相關(guān)的三角形、與圓相關(guān)的角等等.這就要求我們在教學(xué)中，對基本圖形要進(jìn)行系統(tǒng)深入分析，在一個幾何問題中，為什么會想到要應(yīng)用這個基本圖形而不是想到要應(yīng)用另外的一個基本圖形，顯然是決定于這個基本圖形的特征，決定于這個基本圖形不同于其他基本圖形的屬于他本身獨(dú)具的本質(zhì)屬性，決定于這個基本圖形和其他基本圖形的本質(zhì)上的差異，因此，學(xué)生如何能夠迅速抽離出基本圖形，并選取圖形中有用條件進(jìn)行分析就很關(guān)鍵.

有了這種基本認(rèn)識，教師在面對前面的問題“老師，添輔助線有規(guī)律嗎？”“添輔助線的規(guī)律是什么？”“老師，這條輔助線是怎樣想出來的？”“老師，為什么你會想到這樣添輔助線，而我就想不到？”時，就能作出正確的回答：探尋隱去的基本圖形.幾何問題中添輔助線的規(guī)律，只要經(jīng)過認(rèn)真的學(xué)習(xí)，是可以學(xué)會，可以掌握的.

（二）幾何問題中的每一條輔助線都是分析的結(jié)果

對每一條輔助線都能夠講清楚它是怎樣想出來的.題目千變?nèi)f化，唯有思維方法不變，規(guī)律要個人參悟.只能意會幾何問題中的所有的輔助線是從哪里來的.它們都應(yīng)該是由人的大腦想出來的，應(yīng)該是人們經(jīng)過分析、思維得到的，而絕不是從天上掉下來的.因此，幾何問題中的每一條輔助線都應(yīng)該是分析的結(jié)果，從而對每一條輔助線，我們也就能夠明白它是怎樣想出來的.在平面幾何教學(xué)中，教師應(yīng)將每一條輔助線想出來的過程，剖析出來并展示在學(xué)生的面前，在一個幾何問題的分析過程中，在任何一個步驟上，教師都能接受并經(jīng)受得住學(xué)生的提問，并能給予正面、直接和正確的回答.

我們所講的每一道例題，要有意識地采用展示思維過程的方法來進(jìn)行介紹，問題很清楚，有了正確的思維過程，正確的證明過程就是必然的歸宿，而沒有正確的思維過程，正確的證明過程不可能從天上掉下來.正確的思維過程就是：反復(fù)回歸到基本圖形，從復(fù)雜圖形中識別圖形內(nèi)在結(jié)構(gòu)，利用基本圖形性質(zhì)去想象輔助線.

（三）幾何問題中的輔助線是逐步添加出來的

幾何問題的分析和思維過程，是一步一步推進(jìn)的，老師的講課就應(yīng)該是像剝筍一樣，一層一層地剝出來，讓學(xué)生清楚地看到一步一步走向成功的思維過程，這是幾何教學(xué)成功的關(guān)鍵，也是衡量教師教學(xué)水平和教學(xué)能力的一條重要標(biāo)準(zhǔn).因此，輔助線的添加應(yīng)該隨著分析過程的進(jìn)行，分析到哪里，添加到哪里，因而是逐步添加出來的.

尤其是當(dāng)一個問題中出現(xiàn)多條輔助線時，這些輔助線的添加有一個先后的次序和過程，只能是一條一條、有先有后地想出來或添出來，從而也就只能隨著分析過程的進(jìn)行和發(fā)展，逐步添加，逐步完成，也就是分析到哪里就添到哪里，這樣就能夠完整地向?qū)W生顯示每一條輔助線是怎樣想出來的，整個問題的解決又是怎樣一步一步想出來的.在這樣一個前提下，我們還可以進(jìn)一步發(fā)現(xiàn)，幾何問題中的輔助線是既不能少添，這樣問題就會解決不了；也不能多添，因為這時多添加出來的部分就會是說不清楚道理的.

綜上所述，平面幾何基本圖形分析法的獨(dú)創(chuàng)之處，就在于具體而周全地展示每一個平面幾何問題的思維、分析過程，詳盡地介紹每一個平面幾何問題是怎樣一步一步想出來的，基本的平面幾何圖形也是隨著思考的進(jìn)程而被逐個發(fā)現(xiàn)出來的，一條條輔助線也是隨著分析的過程而自然“生長”出來.這樣，就從根本上消除了學(xué)生長期以來存在著的對平面幾何學(xué)習(xí)、實(shí)質(zhì)上就是對添輔助線問題學(xué)習(xí)的畏懼心理 .

［1］陸麗麗.一個基本圖形的拓展與應(yīng)用［J］.中學(xué)數(shù)學(xué)（初中版），2012（9）：79-81.