例析向量題的求解策略

韋 能

(廣西欽州市第二中學，廣西 欽州 535099)

例析向量題的求解策略

韋 能

(廣西欽州市第二中學，廣西 欽州 535099)

由于向量類題型具有“難度大”、“知識跨度大”以及“綜合性強”等特點，一度成為出題者追捧的對象，學生在求解此類問題時常常會因為沒有正確的解題思路而困擾.因此，教師們在教學的過程中就要不斷地給學生們灌輸正確的解題策略，引領學生們深度剖析向量類題型，培養學生們的思維品質，優化課堂的教學質量.

高中數學;向量問題;解題策略

向量題在高中數學中占據著重要的地位.學生們要在向量的定義中，清晰地知道向量的“大小”與“方向”所包含的意義，因為這決定著向量是一種“數”與“形”的結合.因此，向量的許多問題都可以利用“數形結合”的思想去解決.在實際的教學中，教師們就要教會學生們如何充分地利用向量的雙重身份，準確無誤地求解向量類題型.

一、巧借圖形，優化解題

“向量”問題往往可以放到圖象中去解決，學生們在處理平面向量的時候，要充分地利用向量的加法和減法的運算法則以及它們的幾何意義，然后在圖象中表現出來，通過學生們自己作出的圖象，研究圖象中的關系與節點，往往會有利于題目的正確求解，同時也大大地提高了解題的效率.

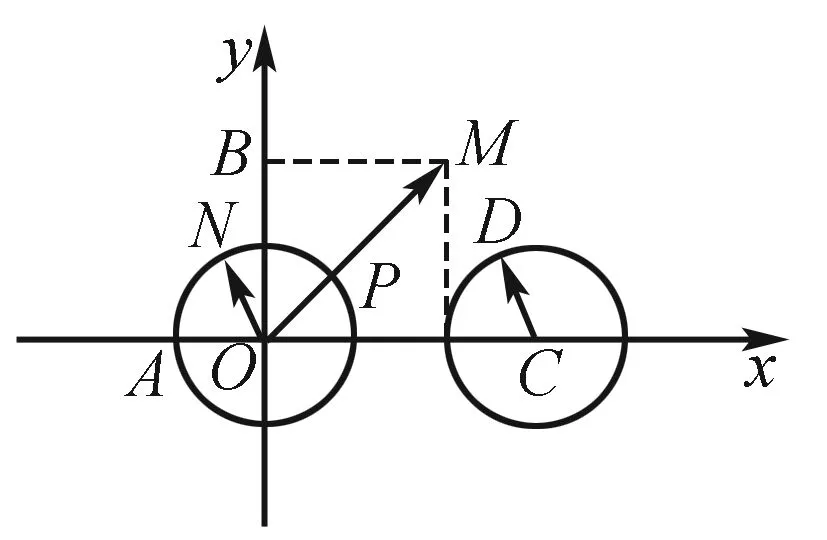
二、靈活建系，巧解難題

在求解平面向量題時，有時可用建立平面直角坐標系這個方法，借助向量的坐標的運算巧妙地解題，這也是“數形結合”思想重要的體現，是學生們必須掌握的解題策略，可大大地減低運算的難度.

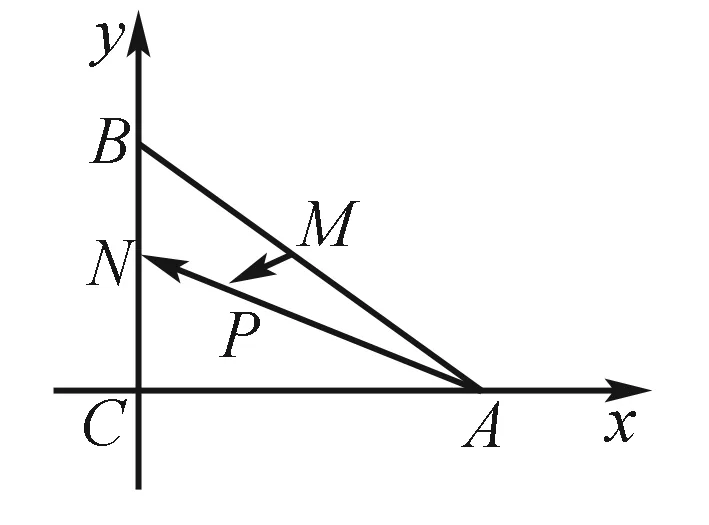
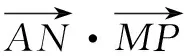
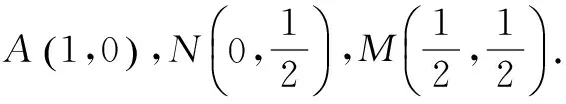
點撥本道題運用到了建立平面直角坐標系去求解的策略，具有一定的綜合性，因此畫出圖形更有利于學生們的解決，理清自己的思路，比較直觀，同時借助線性規劃問題中的平移的技巧，使得難題化簡為易.

三、巧構基底，去繁為簡

“基底”一詞，相信學生們并不陌生，而在向量類題型中，有時候靈活地去構造基底，往往能使得問題化簡為易，提高解題的效率.主要依托理論：選取一組基底e1，e2，利用平面向量的基本定理，將原問題轉化成關于e1，e2的代數問題.

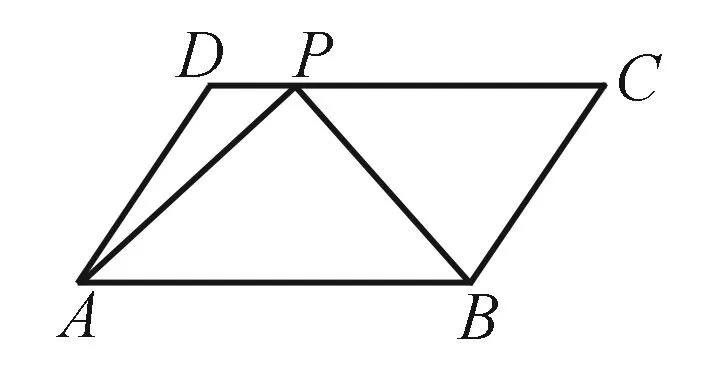
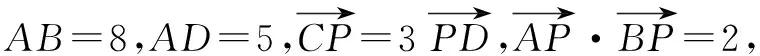
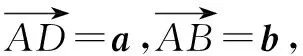
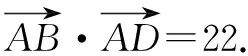
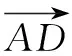
總之，求解向量類問題的方法還有很多，這就需要學生們在學習的過程中不斷地探索與總結，教師們要在學生的解題方法與教學模式之間架設好橋梁，不斷引領著學生，反復地積累，相信在今后遇到平面向量類問題就會迎刃而解！

[1]潘秀梅.坐標法在平面向量問題中的巧用[J].高中數理化，2017(08).

[2]孫香蘭.轉化思想在向量問題中的應用[J].高中數理化，2017(04).

[責任編輯：楊惠民]

G632

A

1008-0333(2017)25-0037-02

2017-07-01

韋能(1980.06- )男，廣西欽州人，本科學歷，中學一級，從事數學教學與研究.