多元最值問題的解決策略探究

崔金華

(江蘇省溧陽市光華高級中學，江蘇 常州 213300)

多元最值問題的解決策略探究

崔金華

(江蘇省溧陽市光華高級中學，江蘇 常州 213300)

本文就常見的多元最值問題，給出了最有效的三種求解方法.

多元最值；解決方法；策略

多元最值問題通常是以含有若干個變量的等式或不等式為條件，求含有這幾個變量的代數式的最值問題.該題型形式一般為:已知F(x,y,…)=0(或者F(x,y,…)≥0)，求G(x,y,…)的最值.

這類問題的解決方法頗多，涉及的知識面較廣，是很多數學思想方法的理想載體，因而成為高考和競賽中倍受青睞的一種題型，并且具有較好的區分度.以下結合具體的實例，探究該類問題的一些常用的求解方法.

一、消元法

例3 (2017揚州期末第14題)已知一個長方體的表面積為48，所有棱長之和為36，則這個長方體的體積的取值范圍為____.

以上三例表明，通常以等式為條件時，可以利用消元法，減少變量個數，再借助其他工具(基本不等式、導數等)求出最值.

二、換元法

解析1 考慮到待求分式上下次數不等，可以考慮借助常數1將目標化為齊次式再來處理.

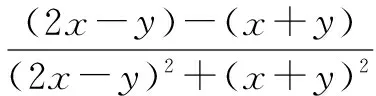
從例5的解法可以看出，對于一個問題的觀察與思考，著眼點不同，解決的方法也不同.三種解法分別從三個不同的角度思考，進行適度換元，在簡化形式的同時也讓問題露出其本質.

三、主元法

以上兩例都是在以幾個變量之間滿足的不等關系為條件的前提下求最值，從解決的方法上我們可以體會到一種“先局部再整體”的思想，也可以理解為“利用不等關系進行消元”.

不等式是高中數學的重點和難點，多元最值問題與不等式聯系最為密切，而“基本不等式”又是這類最值問題常用的工具.在解決這類問題時，對問題所給出的條件進行適當的聯想很有必要，同時結合所要解決的問題，能從不同的角度進行探索與思考，從而找到合理的解決途徑.文中的例5便是一個很好的典范.雖然本文通過若干例題介紹了幾種常用方法，但在解決具體問題時仍需仔細觀察、深入思考、靈活運用，方能有效提高解題技能.

[1]陳瑞琪.突破數學傳統教學模式的一次嘗試[J].上海教育, 1998(12):58-59.

[責任編輯：楊惠民]

G632

A

1008-0333(2017)25-0016-02

2017-07-01

崔金華(1985-)男，江蘇溧陽人，本科，中學二級教師，從事高中數學教學與研究.