深度比較催發深度理解
——以《認識百分數》為例

江蘇南通市通州區金沙小學 張 英

深度比較催發深度理解
——以《認識百分數》為例

江蘇南通市通州區金沙小學 張 英

學生思維能力和解決問題的能力都是建立在理解的基礎上。所以“為理解而教”顯得尤為重要。我們在課應利用各種方法為學生理解性學習提供助力，比較就是一種非常有效的方法。

小學數學 比較 深度理解

數學理解是學生在已有知識經驗的基礎上，通過觀察、比較、分析、推理、概括等活動，對數學知識中的概念、原理、公式、法則等進行解釋，主動建構意義，并在建構意義的過程中，通過同化或者順應，將新知識納入原有的認知結構的一種思維活動。學生思維能力和解決問題的能力都是建立在理解的基礎上。所以“為理解而教”顯得尤為重要。我們在課堂應利用各種方法為學生理解性學習提供助力，比較就是一種非常有效的方法。人們對數學知識概念、原理等的深刻認識，大多都是在比較中實現的。現就以蘇州吳江教科研手拉手活動中聽到的《認識百分數》為例，談一談我的想法。

一、深度比較，深化對百分數意義的理解

當學生的頭腦中對新知的內涵與外延都有比較完整、清晰的認識，說明他們初步建立了概念。認識百分數也是如此，在幫助學生理解百分數意義的過程中，教師多次采用了比較的方法，對同類對象或者異類對象的異同點進行辨別，在層層遞進的比較中幫助學生充分理解百分數的意義，深化了對百分數本質的理解。

1.比較中厘清百分數外延

僅憑一個例子來抽象出百分數的意義，是單薄無力的。而來自學生的鮮活例子往往又是同質、重復的。所以選擇怎樣的材料，教師是深思熟慮的。當學生利用舊有的分數知識解釋氨綸10%、已下載65%、鈣含量3%等的意義之后，教師出示手機屏幕截圖，問學生看到百分數沒有，它表示什么意思？因為有了先前的經驗，學生明白這個21%是目前電量和總電量進行比較的結果，目前電量占總電量的。 教師問：“看到這個信息，我該干嘛了？”學生齊答充電。教師用課件出示電量的變化圖，問學生目前電量大約是總電量的百分之幾？從21%到50%，再到100%，當學生充分理解100%表示什么意思后，教師追問：“如果繼續充電，目前電量可能超過100%嗎？為什么？”學生認為不可能，把總電量看作單位1，再怎么充電都不可能超過單位1。教師說：“那你覺得生活中會不會有超過100%的分數？能舉個例子嗎？”學生不吱聲。這時候教師出示線段圖，連著問了三個問題：學生果園里有75棵桃樹，100棵梨樹，此時桃樹的棵樹是梨樹的百分之幾？根據市場需要果農們又栽了25棵桃樹，現在桃樹是梨樹的百分之幾？如果再栽10棵，桃樹的棵樹是梨樹的百分之幾？隨著數據的變化百分數也在變化，從75%到100%再到110%。這里暗藏著比較，學生舉的例子基本都是部分與整體關系兩個數量之間的比較，而教師補充的例子就非常精心。手機充電情況，讓學生理解了目前電量和未充電量的總和是100%，手機充電不會高于100%，而桃樹和梨樹的關系比較一下子沖破學生的視界，讓學生的視線也變得越來越開闊：兩種獨立量之間的關系是可以超過100%的我們都知道，百分數的內涵是表示兩個數量之間的倍比關系，而外延是這兩個數量可以是 “部分與整體的關系”，也可以是“兩個獨立數量之間的關系”。在鮮活的例子的引領下，學生下意識有了比較，思維不斷跨越，厘清了百分數的外延。

2.比較中明晰百分數內涵

在多個百分數的例子交流之后，教師指著板書：氨綸10%表示氨綸成份占衣服總成份的；脂肪3%表示脂肪含量占牛奶總量的目前電量100%表示目前電量占總電量的；110%表示桃樹棵樹占梨樹棵樹，問學生：“剛才我們交 流了這么多的百分數，它們表示的意義各不相同，但本質是一樣，都表示什么？”學生回答都是一個量和另外一個量比較的結果，都是一個數是另一個數的百分之幾。這段教學又是一次比較，通過適切的具有代表性的一組實例，引導學生類比發現它們的共同屬性，從而抽象出百分數的意義。理解和掌握概念的過程就是在比較中明晰同類事物共同屬性的過程。經過這段教學，百分數的意義浮出水面，但是學生對百分數內涵的理解并不完整。所以教師并不滿足于此，追問學生有沒有什么疑問。學生說：“為什么百分數會叫百分率或者百分比呢？”老師說：“是呀，為什么會叫百分率或者百分比呢？讓我們從幾個例子中體會”。然后教師出示近視率30%等例子，讓學生填一填。引導學生從百分數意義角度去解釋百分率的含義，引導學生將百分數和學過的比的知識進行比較。幫助學生體會近視率30%，既表示近視人數是小學生總數的,也可以表示近視人數與小學生總數的比是30:100。百分數既表示兩個量之間的倍比關系，又表示為后項為100的比。在實例的引領下，學生通過比較分析不僅有效溝通了與比之間的聯系，而且進一步加深了對百分數意義內涵的理解。不僅于此，教師還設計了一道練習題：①一根繩子減去，減去了米。②一噸煤噸，運走了它的。讓學生辨一辨哪些分數可以改成百分數，引導學生把百分數置于整個認知系統中去理解。在選擇的過程中，學生自動比較與分數的聯系與區別，更是對百分數不能表示具體數量，只能表示兩個量之間的一種關系有了特別深刻的理解，至此學生頭腦中的百分數認識內涵更加飽滿、外延更為清晰。這種理解不再是形式上的，而是觸摸到本質的。定義也不再是形式化的定義，而是學生思維上的真理解。

二、深度比較，深化對百分數價值的理解

有了分數為什么又要學百分數？百分數在生活中是否得到廣泛的使用？百分數的價值如何得到凸顯？這些都是我們教學中經常思考的問題。在挖掘百分數作用和價值的教學中，教師又一次采用了比較的方法，在比較中學生腦洞大開、豁然開朗。教師出示三位隊員的投籃情況統計表，問學生誰投得準一些。

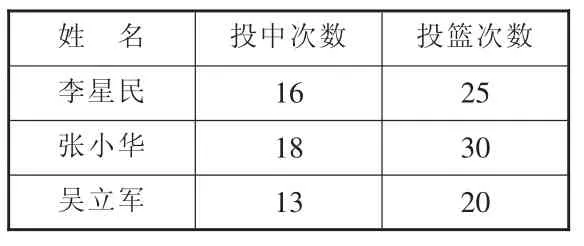
三名隊員投籃情況統計：

經過討論和辨析，學生發現僅關注投中次數不行，關注失球次數也不合理，要比較誰投的準一定要比投中比率，也就是投中次數占投籃次數的幾分之幾。因為給出的數據比較特殊，所以學生自然而然將這些分數通分成分母是100的分數來比較。但是如果遇到一些一般數據呢？如果跟學生說為了便于統計和比較，我們通常把這些分數用分母100的分數來表示，學生能接受化成分母是100的分數再比較的方法嗎？未必！所以，教師又做了第二層次的教學，又出示一組數據。

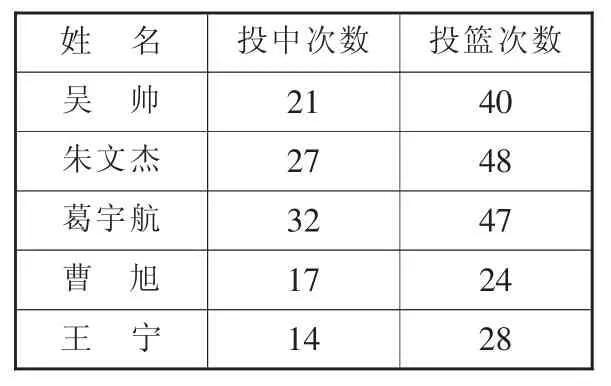
五名隊員投籃情況統計：

在學生分別求出投中次數占投籃次數的幾分之幾后，教師問：“你們打算準備通分嗎？”學生說太麻煩了，教師追問學生：“那怎么辦呢？”學生說：“也可以用小數來比較。”教師追問：“對呀，化成小數也能比較出結果，但是——”一個但是，引發了學生思考，有學生站起來：“如果用小數比的話，就看不出投中次數占投籃次數的幾分之幾了。”教師表揚學生會思考，然后繼續追問：“那有什么辦法既能比出大小，又能看出投中次數占投籃次數的幾分之幾嗎？”經過短暫的小組討論，學生認為可以取這這些小數的近似值，轉化成分母為100的分數比較大小。教師又問：“為什么分母非得是100，為什么不轉化成分母為10或者1000的分數呢？”學生的思維又給激活了，經過討論，學生感覺分母為100精確度比較合適。這時候教師將8位同學的投籃命中率用分母為100的分數展示出來。教師問學生有什么想說的，有學生說比起來非常方便，還有學生站起來說：“我發現有些分數，分子是小數。”教師相機說：“我們以前學的分數里沒有這樣的寫法。所以，我們需要換一種書寫的形式，我們一般寫成百分數的形式。”現在感覺怎樣？學生說非常簡潔，比起來一目了然。讓我們回顧這個過程，兩組數據比較在里面起了決定性的作用，正是比較讓學生思維起了沖突，通分嫌麻煩、小數比較不能看出兩個數量之間的關系，從而逼出了將所有分數轉化成分母是100的分數的需求。學生經歷和體驗了百分數的產生過程，便于統計和比較的特點深入學生內心，深切體會到百分數存在的價值。

烏申斯基認為，比較是一切理解和思維的基礎。本節課，學生的認識經歷了“比較——發現——理解”的過程。在對比中不斷思考，思維清亮明澈。課堂充滿著熱烈的討論、閃爍著思維的火花，不停迸發著細思妙想，對百分數的認識不僅有寬度更有深度！