一種破片側向飛散參量的工程計算模型*
印立魁,趙太勇,侯秀成,陳智剛
(中北大學地下目標毀傷技術國防重點學科實驗室,太原 030051)
一種破片側向飛散參量的工程計算模型*
印立魁,趙太勇,侯秀成,陳智剛
(中北大學地下目標毀傷技術國防重點學科實驗室,太原 030051)
為建立柱形戰斗部破片飛散參量的計算模型,考慮長徑比和破片類型的影響修正Gurney公式構建了戰斗部破片初速的軸向分布模型,修正Shapiro公式構建了精度較高的破片偏轉角模型,所建模型計算值與實驗結果吻合較好,優于現有計算模型。
殺傷戰斗部;初速;偏轉角;工程計算
0 引言
破片飛散狀態直接影響殺傷戰斗部對目標的作用效果。破片初速和偏轉角(或稱拋射角)作為表征破片飛散的基本參量,其計算方法一直受到國內外學者的關注。Randers-Pehrson等[1]系統構建了破片飛散模型,但其初速模型對端部破片的計算值誤差較大;張壽齊[2]和黃廣炎[3]等分別提出破片初速的軸向分布公式,但構建的公式過于復雜,不便于工程計算;Shapiro提出一種破片偏轉角公式[4],但該式的適用性有限;周培基等[5]和秦承森等[6]推導出破片偏轉角的一般計算式,但兩式需要破片速度的詳盡信息,難以用于工程計算。
文中基于一端起爆的圓柱戰斗部破片側向飛散參量的實驗數據,系統構建了計算精度較高的破片飛散模型,并且形式相對簡單,便于工程應用。
1 破片初速的軸向分布模型
現有破片初速軸向分布模型[1-4]均是修正經典初速模型——Gurney公式得到。Gurney公式用于計算長徑比K≥2的戰斗部破片的最大初速,其表達式為:

(1)
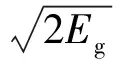
考慮戰斗部裝藥長徑比K和破片類型對破片初速的影響,文中對一端起爆的情況構建如下破片初速軸向分布模型:
v0L=fv(α)·fv(K)·fs·v0
(2)
式中:fv(α)為破片沿初速軸向分布的修正系數,其中α表示破片初始位置在戰斗部軸向的相對位置,α∈[0,1],起爆端α=0;fs為殼體類型對破片初速的影響,對整體殼體取1,對預制破片殼體取值為0.8~0.9;fv(K)為戰斗部長徑比對破片最大初速的修正系數,作者擬合文獻[4]中試驗數據得到:
fv(K)=(1+0.115 6K)-1,K>0.5
(3)
由于端部效應的影響,破片初速沿軸向先增大后減小。分析文獻[7-8]中圓柱裝藥(結構見圖1中的說明)的一端中心起爆的破片初速軸向分布的試驗數據,發現對兩端敞口情況α≈0.65處破片有最大初速,對兩端有端蓋情況α≈0.75處破片有最大初速,即端蓋使破片初速沿軸向的極大值點右移。并構建f(α)的表達式:
fv(α)=1-k(α-Cα)n
(4)
表1給出擬合5組實驗數據得到的k的取值。

表1 式(4)、式(10)中的參量取值
式(1)~式(4)構成了文中的破片初速軸向分布模型。
馮順山軸向初速公式[3]是常用的工程模型,對一端起爆的等厚殼體的圓柱裝藥,其表達式為:
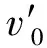
(5)
式中:A=0.361 5,B=1.111,C=0.192 5,F=3.03。
圖1(a)和圖(b)的上圖給出文中模型、馮順山公式計算值與實驗值的對比,可見文中模型精度更高。
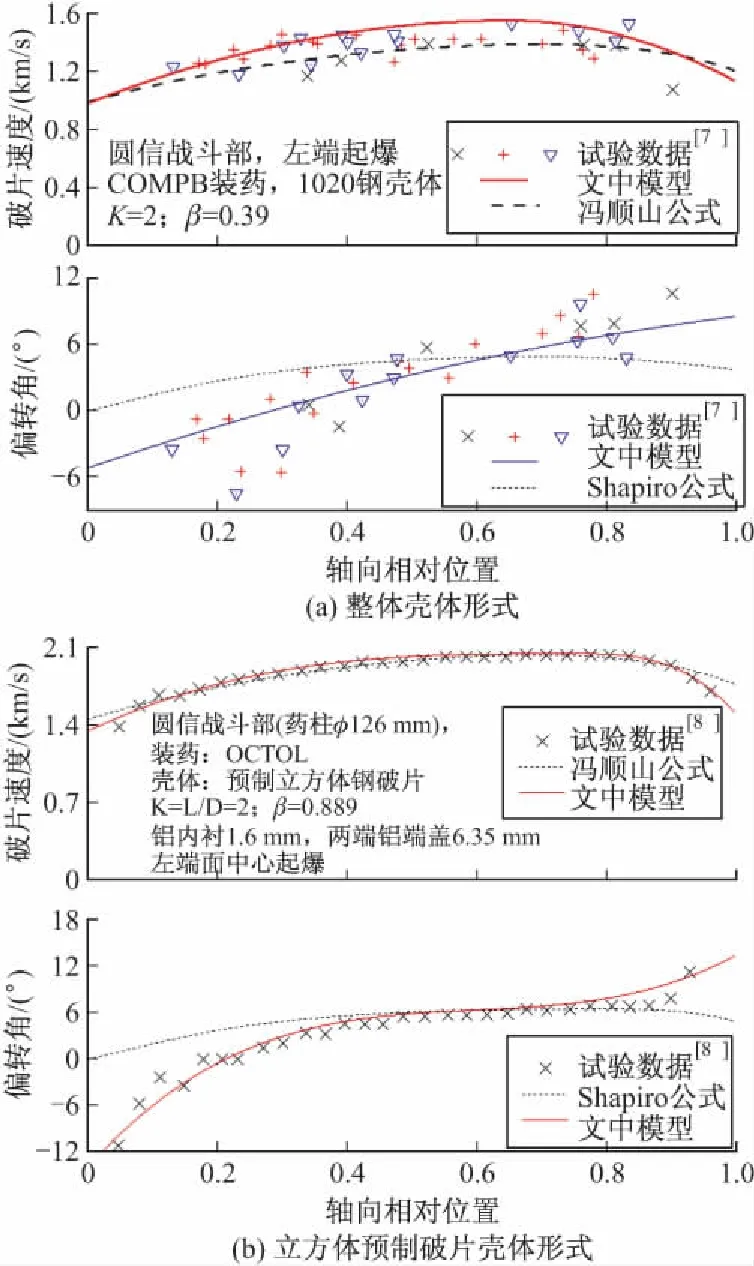
圖1 式(2)、式(5)、式(7)、式(8)的計算值與實驗[7-8]值的比較
2 破片偏轉角模型
計算破片偏轉角的最常用模型是基于Toylor假設推導的Shapiro公式[4],其形式為:
(6)
圖2描述了式(6)中各參量的意義。文中角度單位默認為rad。
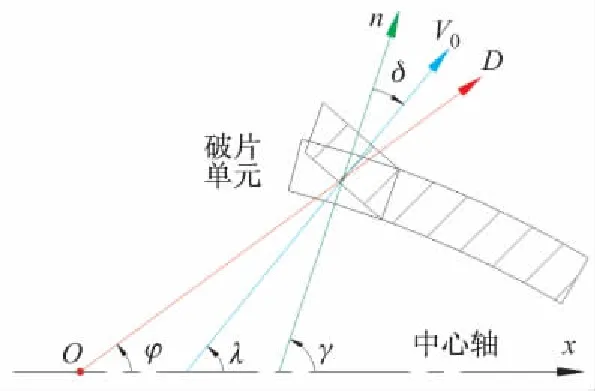
圖2 戰斗部破片偏轉角計算說明圖
圖2中:O為起爆點;n為殼體法線初速度;D為爆轟波速度;v0為破片初速度。
對圓柱裝藥γ=π/2,x=2Kr0α,上式可化為:
(7)
如圖1(a)和圖1(b)的下圖可見,Shapiro公式對邊緣處破片(距兩端面約25%長度內的破片)的計算值與實際結果偏差較大,這主要為端部稀疏波的影響所致。由于Cα處破片初速最大,受端部稀疏波影響最小,文中以此處破片的偏轉角(即δ0(Cα))為基準,對其用f(α)修正表示軸向破片的偏轉角,即:
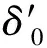
(8)

(9)
結合式(1)~式(4),式(7)~式(9),得:
(10)
分析文獻[7-8]中實驗數據選取:
(11)
表1給出擬合試驗數據所得式中的參數取值。
式(8)、式(10)、式(11)構成了文中的破片偏轉角模型,圖1(a)和圖1(b)的下圖給出文中模型、Shapiro公式計算值與實驗值的對比,可見文中模型計算精度優于Shapiro公式,與實驗值吻合更好。
3 結論
1)Shapiro公式對端部破片偏轉角的計算值誤差較大;
2)構建了戰斗部破片側向飛散參量的計算模型,模型計算值與實驗結果比較吻合,并且形式相對簡單,適于工程計算。
該模型基于K=2的戰斗部的試驗結果得到,對一般戰斗部的破片偏轉角計算有一定的參考價值。
[1] PEHRSON G R.An improved equation for calculating fragment projection angle [C]∥ 2nd International Symposium on Ballistics.1976.
[2] 張壽齊.圓柱形有殼裝藥側向飛散速度分布的預估 [J].爆炸與沖擊,1988,8(3):215-221
[3] HUANG G Y,WEI L,FENG S S.Axial distribution of fragment velocities from cylindrical casing under explosive loading [J].International Journal of Impact Engineering,2015,76:20-27.
[4] 隋樹元,王樹山.終點效應學 [M].北京:國防工業出版社,2000:86.
[5] CHOU P C,CARLEONE J,FLIS W J,et al.Improved formulas for velocity,acceleration,and projection angle of explosively driven liners [J].Propellants,Explosives,Pyrotechnics,1983,8(6):175-183.
[6] 秦承森,劉義,杭義洪,等.周培基拋射角公式的改進 [J].爆炸與沖擊,2005,25(2):97-101.
[7] CHARRON Y J.Estimation of velocity distribution of fragmenting warheads using a modified gurney method:ADA 074 759 [R].1979.
[8] PREDEBON W W,SMOTHERS W G,ANDERSON C E.Missile warhead modeling:computations and experiments:ADA 047 294 [R].1977.
AnEngineeringCalculationModeloftheLateralDispersingParametersofFragment
YIN Likui,ZHAO Taiyong,HOU Xiucheng,CHEN Zhigang
(National Defence Key Subject Laboratory of Underground Target Damage Technology,North University of China,Taiyuan 030051,China)
In order to build the computing model of cylindrical warhead fragment dispersing parameters,considering the influence of the ratio of length to diameter and the type of fragment,the revised Gurney equation was used to construct the axial distribution model of warhead fragment initial velocity.The fragment deflection model with high precision was modified by revised Shapiro formula.The calculated values of the model was identical with the experimental results and had better integrated performace than existing models.
antipersonnel warhead; initial velocity; deflection angle; engineering calculation
10.15892/j.cnki.djzdxb.2017.02.022
2016-04-29
印立魁(1984-),男,河南商丘人,講師,博士,研究方向:彈箭系統仿真。
TJ760
A

