降階控制器性能指標權系數設計方法*

劉文東,李華濱,包為民

(1 北京航天自動控制研究所,北京 100854; 2 北京宇航系統工程研究所,北京 100076; 3 中國航天科技集團公司,北京 100037)

降階控制器性能指標權系數設計方法*

劉文東1,李華濱2,包為民3

(1 北京航天自動控制研究所,北京 100854; 2 北京宇航系統工程研究所,北京 100076; 3 中國航天科技集團公司,北京 100037)

為解決低階反饋控制高階系統的合理性問題,利用基于閉環系統時間尺度特性分析方法,分析了控制性能指標中權系數對六階滾轉駕駛儀系統時間尺度特性的影響,討論了原系統二階、四階控制對反饋狀態的選取與系統當前慢模態的差別,對不同控制的控制性能進行了仿真對比。結果表明:只有通過設計控制性能指標中的權系數,使得反饋狀態變量完全包含當前系統慢模態時,對系統的降階控制才能達到控制性能要求。

兩時間尺度;LQR設計;降階控制;權系數

0 引言

降階控制在控制系統設計中有廣泛的應用。對恰當的被控對象降階模型設計的控制律同樣能夠滿足期望的性能要求。之所以利用降階控制,一方面是由于系統建模的局限性,設計者面對的被控對象模型階數往往低于真實對象階數;另一方面是由于原系統求解復雜,對系統降階設計可以簡化計算,滿足特定任務需求。

廣義上講,幾乎所有的系統都是多尺度系統[1]。對于多尺度系統中最典型的兩尺度問題,可將原系統拆解為兩個子系統分別求解。Shinar在攔截問題[2],Ardema在軌跡規劃問題[3]上都利用了系統的兩尺度特性,然而其對快慢變量的選取依靠的是經驗。Kokotovic分析了線性系統的快慢模態分離方法[4],并證明了對慢模態設計LQR控制器[5]的性能指標,但其控制性能對系統參數變化敏感。

在古典控制方面,Nesline針對LQR降階控制的穩定性問題提出了關于性能指標權系數矩陣的建議[6],但其并未對系統能否使用降階控制這一前提進行驗證。文中利用閉環尺度分塊方法對文獻[7]中六階模型進行了尺度分析,調節尺度差μ觀測系統降階控制包含的控制量,并將其控制性能與二階、四階控制性能對比,得到了設計降階控制所需包含的最少控制量及控制性能對指標權系數的要求。

1 兩尺度數學模型

對于線性定常系統:

y=Cx

(1)

若通過反饋控制使得閉環系統具有兩尺度特性,則可通過一系列變換將式(1)轉化為下式的形式:

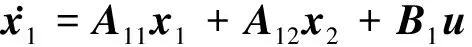
y=C1x1+C2x2

(2)

式中:μ為小于1的小量;x1、x2維度分別為n1×1和n2×1。進而可將其分解為兩個快慢子系統近似。

慢子系統為:

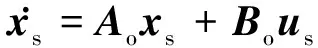
ys=Coxs+Dous

(3)

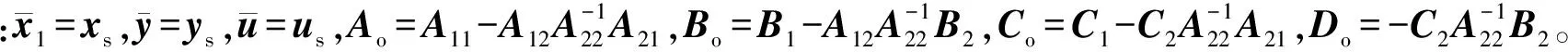
(4)

快子系統為:

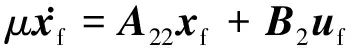
yf=C2xf

(5)

原系統的控制可用兩個子系統的控制復合近似為:

uc=us+uf=Goxs+G2xf

(6)

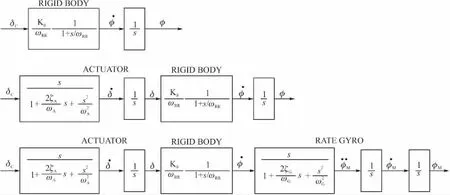
圖1 系統框圖

2 降階控制器設計及性能指標分析

對于輸出調節器問題,控制性能指標為:

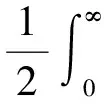
(7)

由文獻[5]知,兩尺度系統復合控制為:

(8)

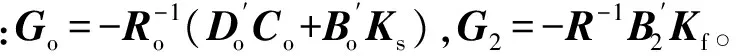
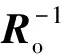
(9)

對于式(9)得到的降階控制,不能依據LQR方法[8]得到其性能指標。文獻[5]指出,通過解Riccati方程:

0=Pr(A-BF)+(A-BF)TPr+FTRF+CTC

(10)

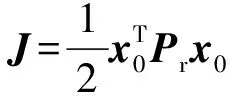
3 降階控制器設計

3.1 時間尺度分析

對系統的認識越深入,系統模型就越復雜。通常只能根據已知的系統模型設計控制器去控制真實的更高階數的系統。而有時雖然已知系統的高階模型,仍希望能夠通過設計低階而有效的控制器對其進行控制。

對于滾轉駕駛儀,二階、四階、六階模型如圖1所示,控制性能指標為:

(11)

表1 模型參數

根據二階、四階模型分別設計的LQR最優反饋控制為:

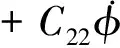
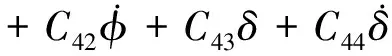
(12)

式中:C21=3,C22=0.103,C41=3,C42=0.127,C43=8.81,C44=0.030 9。

文獻[6]已經指出,若利用δ2c、δ4c控制六階系統,則δCMX必須小于某一數值才能保證系統穩定。雖然此時穩定性得以保證,但使用二階、四階控制的合理性并未得到驗證,即二階、四階控制的控制性能無法保證。

根據多尺度理論[9],高階系統能夠被低階控制的前提即為系統呈現多時間尺度特性。考慮到六階系統可以寫成如下狀態空間形式:

(13)

若令尺度差μ=0.3,依據閉環兩尺度分塊方法,隨著δCMX以0.1°的間隔從0°到10°變化,整個系統呈現的時間尺度特性如表2所示。

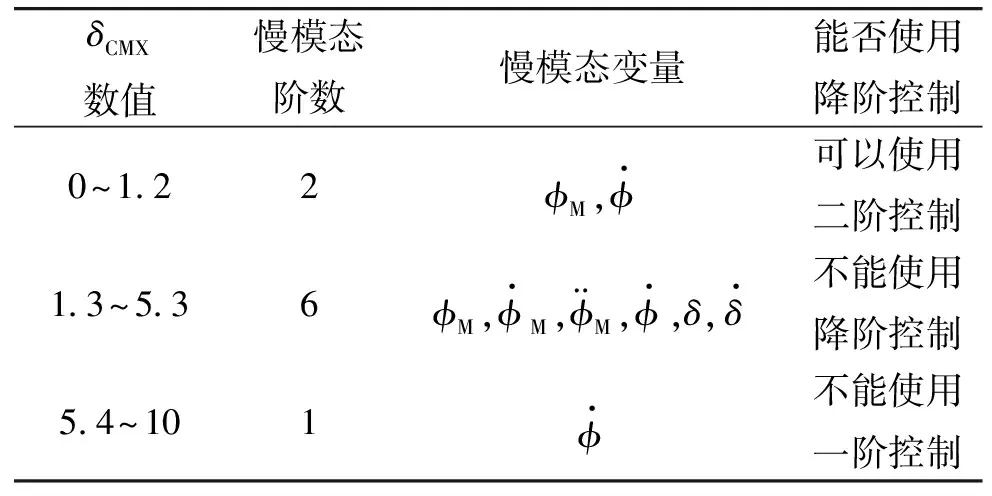
表2 系統時間尺度特性(μ=0.3)

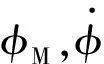
由于尺度差μ直接影響系統快慢模態分塊結果,而該參數的設置應結合具體系統實際情況。故令μ=0.8,重新觀察系統時間尺度特性。

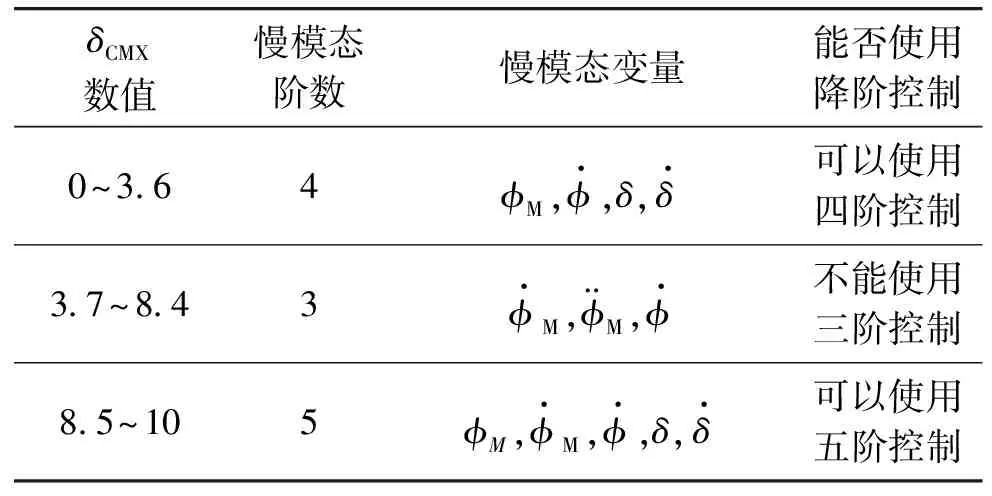
表3 系統時間尺度特性(μ=0.8)

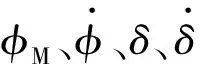
綜合表2、表3可見,尺度差μ越大,慢模態的最低階數就越高,系統能夠使用降階控制的最低階數就越高。同樣也可以看到,系統的時間尺度特性隨控制性能指標中的權系數變化,在針對不同控制系統設計降階控制器時,有必要分析其合理的降階系統階數。

3.2 控制性能對比分析

在上節分析了系統時間特性的基礎上,對二階控制、四階控制、基于閉環尺度特性的降階控制及全狀態反饋的控制性能進行對比分析。

由圖2可見,當δCMX∈(0°,1.2°]時,系統的慢模態與二階控制選取的狀態相符,故初始段Jr位于J2下方,與J2幾乎重合,降階控制性能略優于二階控制。由于此段四階控制包含了所有慢模態及部分快模態,故其控制性能J4要優于J2、Jr,略低于全狀態反饋J6。δCMX位于其他區間時,依據系統時間尺度特性,系統不再適合使用降階控制,即使其目前控制性能指標未發散,也不可預知其發展趨勢,設計δCMX時應避免其值落入該區域。

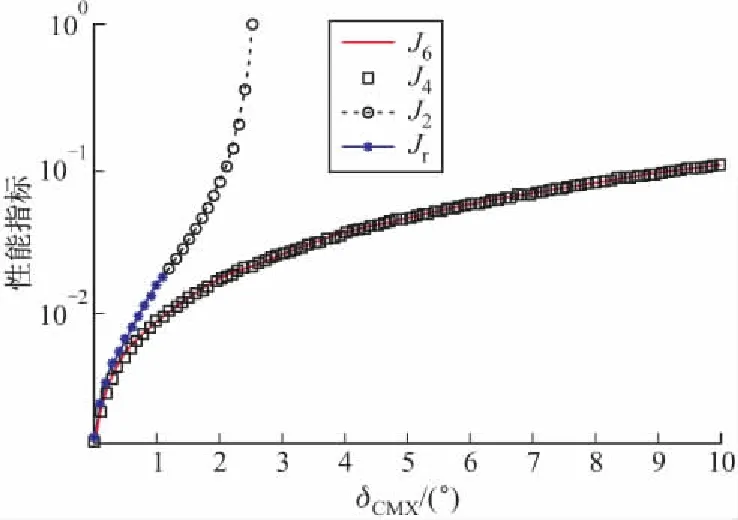
圖2 降階控制與二階、四階控制性能(μ=0.3)

由圖3可見,初始段δCMX∈(0°,3.6°],系統呈現四階慢模態特性,此時利用二階控制相當于主觀降低被控對象階數,其控制性能J2迅速惡化。而四階控制選取的狀態與慢模態相符,故初始段J4與Jr接近。對于中間段δCMX∈[3.7°,8.4°]由于不能使用降階控制,該段不予討論。對于末端δCMX∈[8.5°,10°],降階控制無論階數或者控制性能都更接近全狀態反饋,然而使用降階控制的目的就是為了簡化計算,末端對系統的簡化不大,故選取權系數δCMX時也應避免選取在該段。

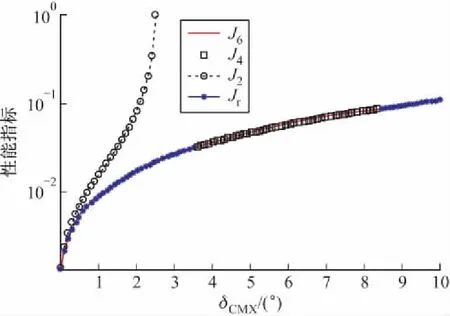
圖3 降階控制與二階、四階控制性能(μ=0.8)

綜合圖2、圖3可知,若通過選取δCMX數值,使反饋的控制量已經包含當前系統全部慢模態,則其控制性能能夠得以保證;若反饋的控制量只包含當前系統部分慢模態,則該控制器設計存在不合理性,其控制效果無法預知。

4 結論

對于特定的控制系統,一旦確定了尺度差μ,即可分析系統控制性能指標中權系數對系統時間尺度特性的影響,由此可以確定適合該系統的低階反饋狀態變量,只有包含全部慢模態的反饋控制才能夠保證系統控制性能,在此基礎上,可根據權系數與系統開環剪切頻率的關系調整權系數保證系統的穩定性,進而得到恰當的低階控制器。

[1] WEINAN E.Principles of Multiscale Modeling [M].北京:科學出版社,2012：1-5.

[2] SHINAR J,FARBER N.Horizontal Variable Speed Interception Game Solved by Forced Singular Perturbation Technique [J].Journal of Optimization Theory and Applications,1984,42(4):630-636.

[3] ARDEMA M D,RAJAN N.Separation of time scales in aircraft trajectory optimization [J].Jounal of Guidance，Control,and Dynamics,1985; 18(2)：275-278.

[4] KOKOTOVIC P V,HADDAD A H.Controllability and time-optimal control of systems with slow and fast modes [J].IEEE Transactions on Automatic Control，1975,20(1)：111-113.

[5] CHOW J,KOKOTOVIC P.A decomposition of near-optimum regulators for systems with slow and fast Modes [J].IEEE Transactions on Automatic Control，1976,21(5):701-705.

[6] NESLINE F W,ZARCHAN P.Why Modern Controllers Can Go Unstable in Practice [J].Journal of Guidance,Control,and Dynamics,1984,7(4):495-550.

[7] NESLINE F W,ZARCHAN P.A classical look at modern control for missile autopilot design [C]∥1982 Guidance and Control Conference.Reston:ARC AIAA,1982:90-104.

[8] 胡壽松,王執銓,胡維禮.最優控制理論與系統 [M].北京:科學出版社,2005:165-169.

[9] RAMNATH R V.Multiple Scales Theory and Aerospace Applications [M].Reston:American Institute of Aeronautics and Astronautics,2010:61-76.

DesignofReducedOrderControllerPerformanceIndexWeights

LIU Wendong1,LI Huabin2,BAO Weimin3

(1 Beijing Aerospace Automatic Control Institute,Beijing 100854,China; 2 Beijing Institute of Astronautical Systems Engineering,Beijing 100076,China; 3 China Aerospace Science and Technology Corporation,Beijing 100037,China)

To solve rationality problem using low order feedback to control high order system,a method of system decomposing based on closed-loop time scale characteristic was used.The influence of performance index weights on sixth order roll autopilot system characteristic was analyzed.The differences of feedback state choosing between second order,fourth order and current system reduced order were discussed,and the performances were simulated and compared respectively.The results show that:Only if the feedback states contain all slow modes through design of performance index weights,the reduced control can achieve the performance requirement.

two-scale system; LQR design; reduced control; weights

10.15892/j.cnki.djzdxb.2017.02.003

2016-05-30

國家自然科學基金青年基金(61403355)資助

劉文東(1987-),男,遼寧大連人,博士研究生,研究方向:兩尺度系統、飛行控制。

O232

A