“直觀想象”在全國卷函數試題中的應用探析*

林麗娟 林新建

福建省漳州第一中學 (363000)

“直觀想象”在全國卷函數試題中的應用探析*

林麗娟 林新建

福建省漳州第一中學 (363000)

“直觀想象”是高中數學核心素養的重要內涵.

“直觀想象”是指借助幾何直觀和空間想象感知事物的形態與變化，利用圖形理解和解決數學問題的過程.

“直觀想象”主要包括：借助空間認識事物的位置關系、形態變化與運動規律；利用圖形描述、分析數學問題；建立形與數的聯系；構建數學問題的直觀模型，探索解決問題的思路.

下面以全國卷函數試題為例，就“直觀想象”在解題中的應用作一探析，以饗讀者.

1.運用“直觀想象”引領圖形特征的感知

運用“直觀想象”策略，可以較好地引領函數圖形特征的感知，進而借助圖形特征可將問題輕松予以解決.

例1 (2009年高考新課標卷Ⅰ理科第9題)

已知直線y=x+1與曲線y=ln(x+a)相切，則a的值為( ).

A．1B．2C． -1D．-2

解析：本題若依常規方法求解有一定的運算量，但若運用“直觀想象”策略予以求解根本不用計算，瞬間可得答案.

由“直觀想象”可知：函數y=ln(x+1)的圖像在直線y=x+1的下方，從而知欲使得曲線y=ln(x+a)與直線y=x+1相切，則曲線y=ln(x+a)必是曲線y=ln(x+1)向左平移而得，結合選項容易排除A、C、D，故選B.

例2 (2013年高考新課標卷Ⅰ理科16題)

若函數f(x)=(1-x2)(x2+ax+b)的圖像關于直線x=-2對稱，則f(x)的最大值是___________.

其實，若運用“直觀想象”策略對函數的圖形特征作感知，可將問題輕松予以解決，運算量也很小.

由“直觀想象” 知函數f(x)有兩個零點1，-1，又f(x)的圖像關于直線x=-2對稱，故f(x)另有兩個零點-3，-5，所以f(x)=-(x-1)(x+1)(x+3)(x+5).

再運用“直觀想象”對f(x)的圖像作感知，可知若f(x)的圖像向右平移兩個單位，其最大值不會改變，于是我們可將求函數f(x)的最大值轉化為求函數h(x)=-(x-3)(x-1)(x+1)(x+3)的最大值了.

至此，直接配方即得h(x)=-(x2-5)2+16，故f(x)的最大值為16.

與高考參考解答比較，這樣的解法另辟蹊徑，輕松快捷，凸顯了“直觀想象”在引領函數圖形特征感知、簡化解題途徑上的重要作用.

2.運用“直觀想象”引領形數關系的建立

運用“直觀想象”策略，可以較好地引領形數關系的建立，進而借助形的直觀可將函數問題輕松予以解決.

例3 (2012年高考新課標卷Ⅰ理科21題)

(Ⅰ)求f(x)的解析式及單調區間；

解析：本題難在第(Ⅱ)問，許多考生不知從何入手，望題興嘆而已.

其實，若能運用“直觀想象”策略建立起形與數之間的關系，問題可輕松獲得解決.

由“直觀想象”知，要使上式對一切實數x∈R成立，函數y=ex的圖像必須在函數y=(a+1)x+b圖像的上方，故必須有a+1>0，因此，要使(a+1)b最大，必須b>0.

再由“直觀想象”知，直線y=(a+1)x+b必須與函數y=ex的圖像相切.至此問題就容易解決了.

設切點為P(x0,y0)，則y0=ex0=(a+1)x0+b，且ex0=a+1.聯立可得x0=ln(a+1)，b=(a+1)-(a+1)ln(a+1).

故(a+1)b=(a+1)2-(a+1)2ln(a+1).

與高考參考答案比較，這樣的解法另辟蹊徑、簡潔優美，使我們感到——運用“直觀想象”策略可輕松引領形數關系的建立，這樣不但回避了分類討論帶來的麻煩，而且思維更加流暢、更容易接近問題的本質.

3.運用“直觀想象”引領解題思路的生成

運用“直觀想象”策略，可以較好地引領解題思路的自然生成，使得難題的解決進行得輕松自在，輕而易舉.

例4 (2010年高考新課標卷Ⅰ理科21題)

設函數f(x)=ex-1-x-ax2.

(Ⅰ)若a=0，求f(x)的單調區間；

(Ⅱ)若當x≥0時f(x)≥0，求a的取值范圍.

解析：本題第(Ⅱ)問很難，運用常規方法如“參數分離”等均無法將其解決，怎么辦？

其實，若運用“直觀想象”策略對函數的圖像作探究，不難探索出問題求解的簡潔思路，將問題的解答臻于完美.

因為f(0)=0，即f(x)的圖像過原點，而f(x)≥0對一切x≥0都成立，所以由“直觀想象” 知，f(x)的圖像在x=0右側附近必須遞增，所以f′(x)≥0對x=0右側附近成立.

又因為f′(x)=ex-1-2ax，f′(0)=0，所以同樣由“直觀想象”知，f′(x)的圖像在x=0右側附近也必須遞增，從而f″(x)≥0對x=0右側附近成立.

有了這個發現就好辦了，接下來我們只要證明：

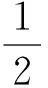
證明：由f(x)=ex-1-x-ax2知，f′(x)=ex-1-2ax，f″(x)=ex-2a.

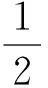
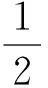
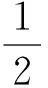
由于“直觀想象”，我們猜想出a的范圍，進而將問題轉化而輕松求解，凸顯了“直觀想象”在探索問題解決思路、簡化難題求解途徑上的重要作用.

“直觀想象” 在數學解題中有著重要的作用，在直觀想象核心素養的形成過程中，學生能夠進一步發展幾何直觀和空間想象能力，增強運用圖形和空間想象思考問題的意識，提升數形結合的能力，感悟事物的本質，培養創新思維，平時教學和高考復習都應予以足夠的重視.

*本文是2016年度漳州市基礎教育課程教學研究課題“基于全國考試的高三有效性復習研究”的研究成果.