一個三角不等式的求解及推廣

史建軍

江蘇省丹陽高級中學 (212300)

一個三角不等式的求解及推廣

史建軍

江蘇省丹陽高級中學 (212300)

1.問題的提出及求解

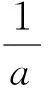
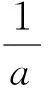
由柯西不等式可知：

2.問題的變形

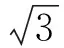
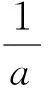
3.問題的推廣

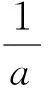
“=”當且僅當圓內接n邊形A1A2…An為正n邊形時成立.

圖1

證明：如圖1，設圓心為O，連結A1O,A2O,…,AO，設∠A1OA2=θ1,∠A2OA3=θ2,…,∠AnOA1=θn，則由余弦定理有

l21=R2+R2-2R·Rcosθ1，l22=R2+R2-2R·Rcosθ2，…，l2n=R2+R2-2R·Rcosθn.

引理任意四面體的各棱長平方和不大于其外接球半徑平方的16倍，即：設四面體ABCD的6條棱長分別為l1,l2,…,l6，外接球半徑為R，則l21+l22+…+l26≤16R2.“=”當且僅當四面體的重心和外心重合時成立.

證明：以四面體的外接球球心(外心)為原點建立空間直角坐標系，則各棱長平方和為