注重過程教學 完善認知結構

宋振蘇

江蘇省大港中等專業學校(222043) 周法青江蘇省連云港開發區高級中學 (222067)

注重過程教學 完善認知結構

宋振蘇

江蘇省大港中等專業學校(222043) 周法青江蘇省連云港開發區高級中學 (222067)

新課程標準中關于知識三維目標是：“知識與技能，過程與方法、情感、態度與價值觀”，這說明強調教學的過程觀是新課程標準所要突出的基本教學理念之一.現代認知心理學則認為數學知識教學的過程是一個動態的生成過程，是教師指導學生學習數學知識和技能的雙邊活動過程，是學生對數學知識的發生與發展的認識過程；而認知結構則是學生在學習數學知識時在頭腦中逐漸形成的認知模式結構，是客觀、內在的心理范疇內的東西，因此教學的過程也是學生在教師的組織和引導下歷經感受和理解所學知識并逐步改造和完善自身數學認知結構的過程，基于這些內涵的理解，這就要求教師在數學課堂教學的實踐中，應注重數學知識的過程教學，以此來發展、完善和優化學生的認知結構.本文擬結合課堂教學的實踐就注重過程教學，完善和優化學生認知結構談點粗淺體會和認識.

一、注重知識發生過程是完善認知結構的前提

眾所周知，數學是“思維的體操”，數學教學的過程是感受知識的形成過程發展學生思維能力的過程，教學過程中如果只為完成教學任務，或為節約時間，將一些思維價值豐富的知識發展和生成的過程簡化和揚棄了，只留下一些本質的邏輯的結論，掩蓋了思維的過程，將知識和方法作為結果直接拋給學生，這樣學生就沒有機會歷經和感受知識的形成過程，就會使學生對這些知識缺乏一個完整的認識過程，使學習變成一種枯燥的沉重的記憶負擔，當然也就形成不了完善的數學認知結構.

例如，在教學“三角函數的誘導公式”這一內容的過程中，如果只是簡單的將幾組公式介紹一下，然后拋給學生讓學生去死記硬背，甚至將其編成順口溜“奇變偶不變，符號看象限”讓學生去背，這樣就會坐失培養學生數形結合能力和探究能力的大好契機，同時學生也形成不了一個完善的認知結構，一到做題時就去翻課本，找公式，使學生對這部分知識的學習成為負擔和包袱；反之，如果借助單位圓，運用所學知識，數形結合，歷經這幾組公式的條件的分析和推導過程，這樣在公式推導出來的同時，所學的知識和方法不僅能得以加強和鞏固，思維的能力也得到了鍛煉與訓練，同時對公式的內涵與結構形式也留有較為深刻的認識，這樣學生的認知結構也得到及時的完善和優化.

因此，在一些概念和公式的課堂教學過程中，要精心設計其產生與發生的過程，努力創設問題情境，充分展示知識產生、發生的全過程，以達優化和完善學生認知結構之目的.也就是說，教學過程中強調揭示數學知識的發生過程不僅有利于學生思維能力的訓練，體現“思維的體操”的功能，而且更有利于學生掌握知識的來龍去脈，構建完善的認知結構.

二、注重知識深化過程是完善認知結構的主干

知識的發展、深化過程是知識形成過程中最精彩、最關鍵的環節，是完善學生認知結構的主干環節.在這一教學過程中，既要對數學概念、公理、定理、公式、法則等數學知識的發現、提出、抽象、概括、推證過程作出通俗的解釋，又要對其作出本質的揭示，進而闡明條件與結論的邏輯聯系.也就是說在實際的教學過程中，既要精心設置系列問題，合理創設問題情境，也要充分暴露和展示這些知識的產生的思維過程，解決學生在知識認知上的認識沖突，從而完善和優化學生的認知結構.

例如，在教學雙曲線這一概念時，為了加深對雙曲線定義的內涵和外延的理解和掌握，可設置如下一組系列問題：

(1)若將雙曲線定義中的“小于|F1F2|”換為“等于|F1F2|”，其余的不變，則動點的軌跡是什么？

(2)若將雙曲線定義中的“小于|F1F2|”換為“大于|F1F2|”，其余的不變，則動點的軌跡是什么？

(3)若將雙曲線定義中的“絕對值”去掉，其余的不變，則動點的軌跡是什么？

(4)若令雙曲線定義中的“常數為零”，其余的不變，則動點的軌跡是什么？

(5)若將雙曲線定義中的“小于|F1F2|”去掉，其余的不變，則動點的軌跡是什么？

通過對這一組系列問題的解答和辯析，既掌握了雙曲線的定義，也深刻理解了雙曲線定義的內涵和外延，同時也解決了一些與雙曲線定義有關的軌跡問題.

這里通過設置系列問題達到了對數學概念知識的深刻認識和理解的思維展示，這組系列問題對深化和鞏固雙曲線這一概念起到了重要的作用，與此同時，學生的認知結構也得到優化和完善.

從以上教學過程的實踐可以看出通過對知識的發展、深化過程，使學生在頭腦中編織出知識的網絡結構，構建起知識的完整框架和結構，使知識結構與認知結構更加優化和完善.

三、注重知識應用過程是完善認知結構的核心

數學問題的解決過程，也就是數學知識的探索和應用過程，著眼于數學知識的應用就是要求學生用所學的知識、方法去分析問題和解決問題，實踐證明只有在應用數學知識解決數學問題的這一過程中，學生認識和理解所學數學知識間的內在聯系才能得到更加深刻感悟和理解，才能對具有觀念性的數學思想與方法領悟得更加深刻，進而有效地從整體上更好地把握和認識數學知識，建構和完善合理優化的數學認知結構.

其實在解答這一問題的過程中，忽視了運用等比數列的前n項和公式時，一定要對公比分q=1和q≠1兩種情形進行分類討論這一環節，因此產生了錯誤的答案，其實當q=1時，也符合本題的題設，故所求數列的公比為q=1和q=-2.

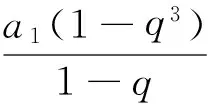
因此應用所學知識解決問題的教學過程，就是對原有的數學知識進行加工、梳理和辨析的過程，同時也是對新知識進行理解和鞏固的過程，更是認知結構得以完善和優化的過程.

四、注重思想方法形成過程是完善認知結構的歸宿

數學知識是“載體”，而思想方法則是“靈魂”，數學思想方法的形成過程就是數學知識在應用的過程中逐漸產生與形成的，是數學能力逐步運用的過程，也是良好的數學認知結構形成與完善的過程，因此在數學課堂教學的過程中，特別在應用數學知識解決問題時所運用的靈魂性思想和方法與形成和訓練而成的能力則是數學課堂教學的最終目的和歸宿，知識在運用的過程中不斷得到補充和完善，并向著更深、更高層面發展，這也是數學課堂教學的高層次追求.

例如，在解答問題“(2007年廣東卷壓軸題)設a∈R，若函數f(x)=2ax2+2x-a-3在區間[-1,1]上有零點，求實數a的取值范圍”時，常規方法是運用二次函數的知識直接求解，不僅運算較為繁難，而且解答過程冗長，產生這一思維誤區的原因是轉化不合理、不到位而造成的.其實這里可讓學生運用函數方程思想，即先將參數a從方程中分離出來，建構出新的函數，再巧妙運用換元變形可得如下簡捷、巧妙的解法：

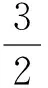
通過本題的教學不僅簡捷、巧妙地解答了這個問題，而且幫助學生通過對本題的分析求解，使學生形成了“化歸與轉化”、“函數與方程”、“數形結合”、“分類與整合”等數學思想和方法，完善和優化了學生在思想與方法等方面的數學認知結構，為以后的解題提供和儲備了重要的數學思想和方法，同時，在這些教學思想方法的形成與運用的過程中，學生的能力也得到提高和升華，達到課堂教學的最終目的和歸宿.

綜上所述，從現代認知心理學角度來看，數學知識的教學過程就是改造和完善學生認知結構的過程，也是知識的發生、發展、深化和應用的過程，更是數學思想方法螺旋上升和循環生成的過程，因此注重數學知識的過程教學有著極其重要的現實意義.