斷環(huán)區(qū)域上的二重積分

傅守忠，梁小芬

（肇慶學院 數(shù)學與統(tǒng)計學院，廣東 肇慶 526061）

斷環(huán)區(qū)域上的二重積分

傅守忠，梁小芬

（肇慶學院 數(shù)學與統(tǒng)計學院，廣東 肇慶 526061）

本文討論了將斷環(huán)區(qū)域上的二重積分化為累次積分的計算方法，并給出幾個利用該方法計算會變得相對簡單的實例．

斷環(huán)區(qū)域；二重積分；累次積分

0 引言

1 斷環(huán)區(qū)域上二重積分的計算公式

引理1[1-2]若f(x,y)在xy平面的閉區(qū)域D上可積，又設極坐標變換

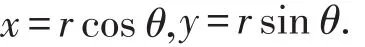
將rθ平面上的區(qū)域Δ變換為xy平面上的區(qū)域D,則

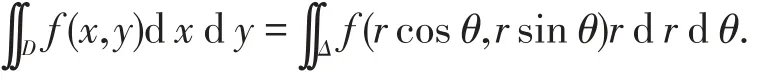
定理1[1]249設xy平面中的區(qū)域D為斷環(huán)區(qū)域，即在極坐標下可表示為

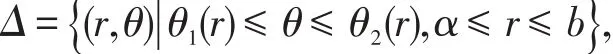
證 由引理1和二重積分化累次積分的計算方法可直接得到.

推論1 被積函數(shù)f(x,y)≡1的二重積分等于積分區(qū)域的面積，特別在上述定理的區(qū)域中

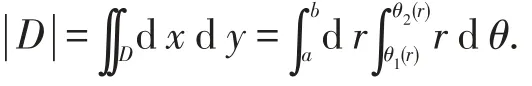
2 斷環(huán)區(qū)域上二重積分示例

例1 求區(qū)域D的面積，其中D于極坐標下是在r=1和r=2圍成的環(huán)內，被極軸θ=0和曲線所截部分(見圖1)．

解 根據(jù)第1節(jié)中的推論，區(qū)域D的面積為

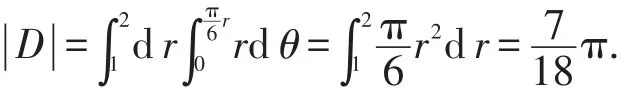
注：若用θ-型區(qū)域，則

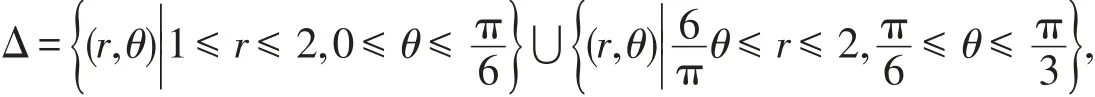
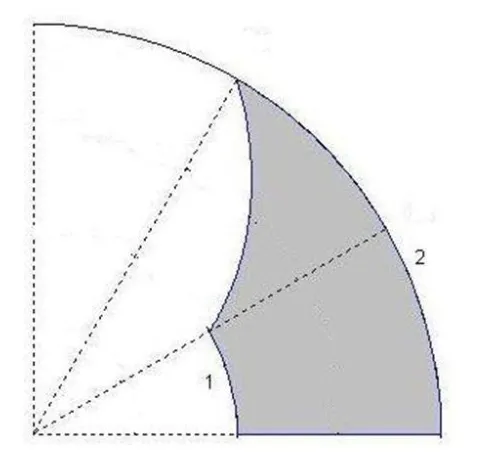
圖1 例1的積分區(qū)域

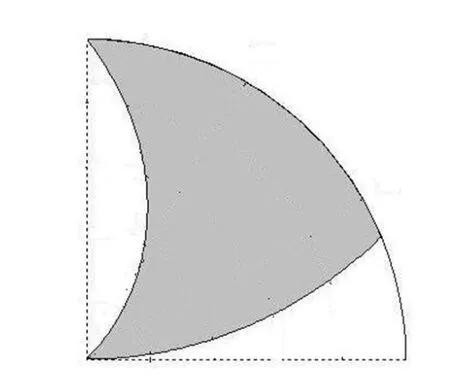
圖2 例2的積分區(qū)域

解 區(qū)域D在極坐標下可以表示為

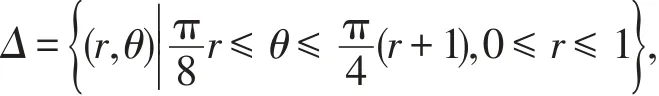
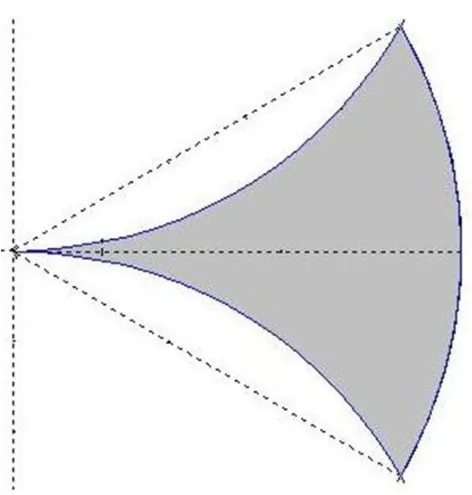
圖3 例3的積分區(qū)域

解法1（將D看做R-型區(qū)域） 由于積分區(qū)域對于變量y是對稱的，而被積函數(shù)又是y的偶函數(shù)，因此只需計算上半區(qū)域的積分.又因圓x2+(y-1)2=1的極坐標方程為r=2sin θ,所以區(qū)域D的上半部分在極坐標下可以表示為

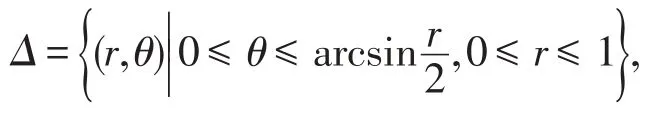
根據(jù)定理1得

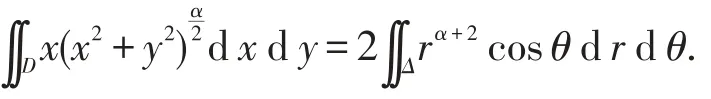
注意到坐標原點(0,0)(即r=0)是被積函數(shù)唯一可能的瑕點（當α＜-1時），先考慮區(qū)域

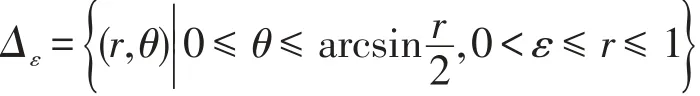
上的積分，

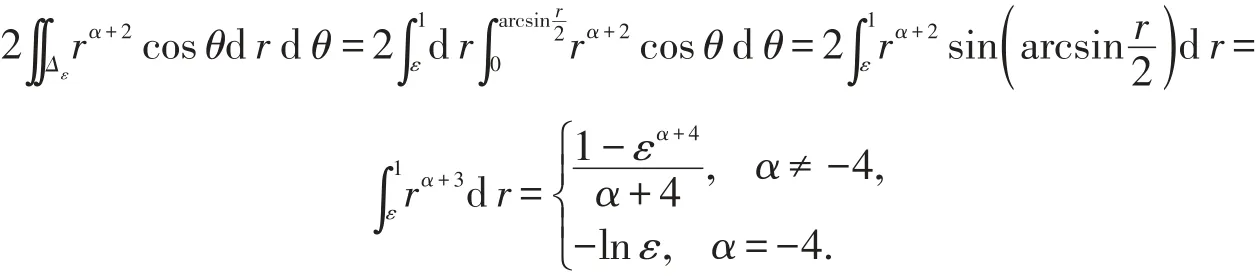
再令ε→0+,上式當且僅當α＞-4時收斂，此時

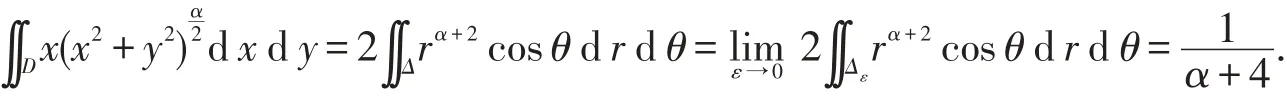
解法2（將D看做θ-型區(qū)域） 區(qū)域D的上半部分在極坐標下也可以表示為

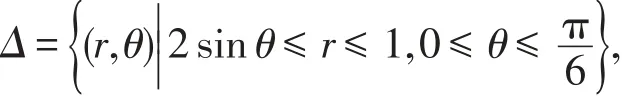
類似地，先考慮區(qū)域Δδ上的積分，其中

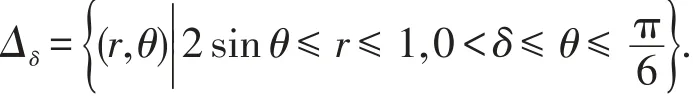
情形1:當α=-3時，

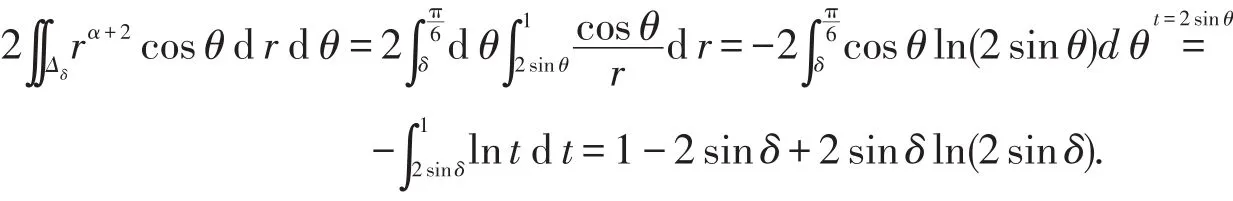
當ε→0+時，上式收斂，且其極限為1.

情形2:當α=-4時，

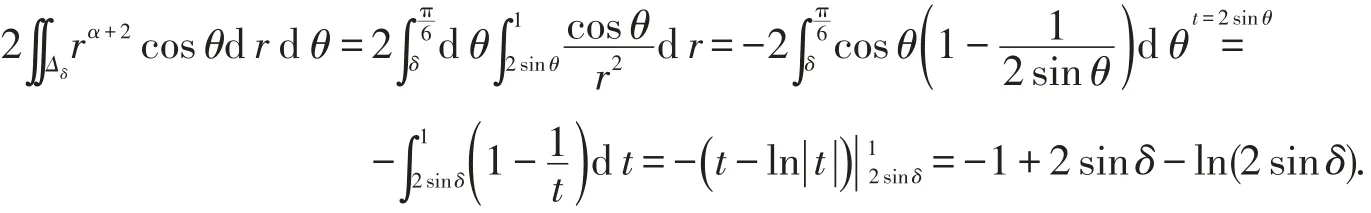
當δ→0+時，上式極限不存在.

情形3:當α≠-3且α≠ -4時，

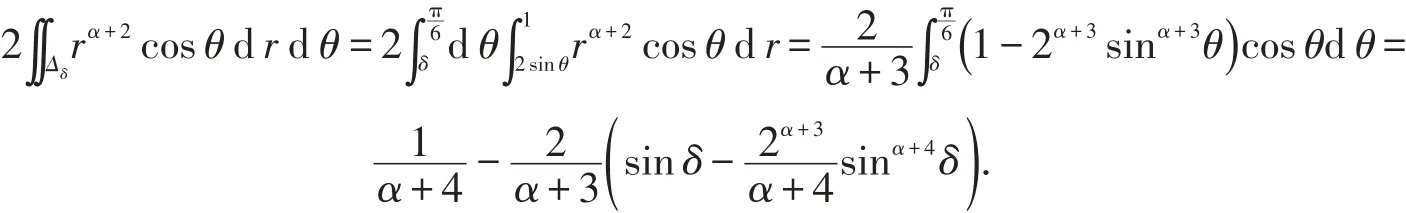
令δ→0+,則在該情形中當且僅當α＞-4時收斂，且

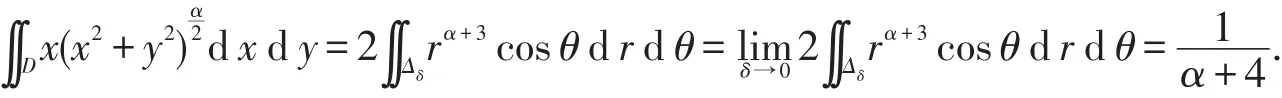
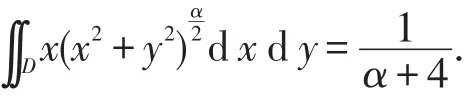
注：在直角坐標下計算，該積分所化成的累次積分非常復雜；在極坐標下，用θ-型區(qū)域計算比用R-型區(qū)域計算要復雜許多.

綜合情形1～3可得，當且僅當α＞-4時原積分收斂，且

3 小結

本文所構造的3個二重積分的例子，無論是在直角坐標下化累次積分，還是在極坐標下化作先對r再對θ的累次積分，都比較繁瑣；而化成先對θ再對r的累次積分，則相對簡捷．

[1] 華東師范大學數(shù)學系.數(shù)學分析:下冊[M].北京:高等教育出版社,2011:211-243．

[2] 歐陽光中,朱學炎,金福臨,等.數(shù)學分析:下冊[M].3版.北京:高等教育出版社,2007:269-315．

The Double Integrals with Broken Ring Domain

FU Shouzhong,LIANG Xiaofen
(School of Mathematics and Statistics,Zhaoqing University,Zhaoqing,Guangdong 526061,China)

The calculation of the double integral on broken ring domain by using repeated integral are discussed and some examples to apply this method are given.

broken ring area;double integral;repeated integral

O172.2

A

1009-8445（2017）05-0005-04

2016-12-23

廣東省高校教學質量與教學改革工程建設項目(2014JP217)

傅守忠(1966－),男,內蒙古卓資人,肇慶學院數(shù)學與統(tǒng)計學院副教授,博士.

（責任編輯：陳 靜）