滲透數學思想方法“三步曲”

陳美青

摘要：教師對學生數學思想方法的滲透，要經過循序漸進和反復訓練。作為教師，就要明確對所教內容中所蘊含的數學思想方法，在備課時要從課堂導入、新知識教學、練習鞏固等幾個方面在課堂上滲透數學思想方法。

關鍵詞：課堂教學；有效滲透；數學思想；方法

2011年版的數學課程標準強調：學生的學習應由“雙基”變為“四基”，即在掌握數學基礎知識和基本技能的基礎上，學生還要獲得基本活動經驗和基本思想方法。學生學習數學的目的已不再是以簡單的“接受數學知識”為核心，培養基本活動經驗和基本思想方法成為數學學習的重中之重。作為教師，應啟發學生思維，逐步積累和形成數學思想方法，重在“滲”，著眼于“透”，潛移默化地影響學生。在小學數學教學中如何有效發展學生數學思想方法呢？本人結合教學實踐，淺談幾點做法。

序曲促體驗

小學生注意力易分散，為了吸引學生，讓學生保持良好的學習狀態，教師要精心設計導入這個環節，既能激發學生的學習興趣，又讓學生初步感悟數學思想，收到一箭雙雕的作用。如在教學“圓的面積”時，筆者是這樣導入新課的：讓學生先復習已學過的圖形的計算公式，并說說這些公式是怎樣推導出來的，及時引入轉化思想，并告訴學生，今天我們就繼續用這種轉化的方法來探討圓的面積計算公式，因為目標明確，且有一定的學習活動經驗，學生在操作活動中很快發現了拼成的近似長方形與圓的關系，得心應手地推導出了圓的面積計算公式，并進一步加深了對“轉化”思想的認識，并從中感悟了極限思想。因此教師備課時，首先要讀懂教材，讀透教材，找出教材中哪些部分可以作為培養學生思想方法的素材，深入理解教材；其次，在讀懂教材的基礎上，應深入理解“隱藏”在數學知識后的數學思想方法，有意識地訓練學生運用數學思想方法，解決數學中的實際問題。充分體現“教學設計成為編者意圖的再現和再創造”的作用。

探究新知中培養數學思想

引導學生對于新知識的探究，是數學教學中的重點、難點，是學生有效掌握數學知識、學習數學技能的過程，更是培養學生產生并運用數學思想方法的過程。即在數學問題的探究發現過程中，運用“創設情境—建立模型—解釋應用與提升”的學習模式，讓學生在掌握數學知識技能的同時，更要真正領略數學的精髓——數學思想方法。

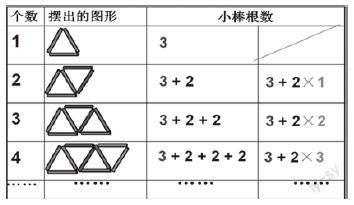
如在教學《圖形中的規律》時，筆者讓學生探究100個連接三角形的規律時，先讓學生討論，達成共識，必須選取較小的三角形來研究，并填寫學習單。用小棒擺成的三角形個數（如下圖）列式計算。讓學生通過同桌合作的方式，擺小捧、觀察比較、合作探究等實踐活動，認真探索擺連接三角形的數量與小棒總數的關系，找出了其中的規律。學生從具體圖像表述——數學語言表達——抽象數學符號語言的建模過程中，體悟到“數形結合”“化繁為簡”“一一對應”“圖像抽象化”等數學思想方法，并感受到成功的喜悅。因此，作為教師，不能為了解題而解題，應對解題活動加以指導，要在解題過程中教給數學思想方法，恰當運用這些方法，不僅能提高解題效率，還能激發學生強烈的求知欲與創新精神。

復習與鞏固

數學知識的掌握，數學技能的培養，學生智力的開發與數學思維的培養都要輔以適量的練習才能得以鞏固和深化。教學課堂的練習主要是鞏固新知，讓學生在形成技能的同時，向數學能力轉化。因此，教師在練習題的設計中，不僅要體現具體知識和技能的訓練，更要有明確的數學思想方法的教學要求。

例如，在《圖形中的規律》練習中，學生在探究連接三角形的排列規律后，教師提問：同學們用“數形結合”的方法擺小棒，用列表格的方法進行整理，探究了連接的三角形數量與小棒數量的關系與規律，它們有什么聯系嗎？如果用小棒擺成四邊形、五邊形或者其他圖形，所擺圖形的數量與小棒的數量又有什么規律可循呢？在這個環節中，可以大膽放手，讓學生通過具體操作，并加以想象、推理，概括歸納出連接正四邊形、正六邊形或其他圖形所擺圖形的數量與小棒數量的規律。從這些訓練中，學生理解和掌握基本數學知識，培養基本數學技能，獲得基本數學經驗，培養學生類比推理、抽象概括能力。教師應該在練習設置中，通過練習不斷探索和總結，從中找到共性，讓學生在學習中培養最本質、最有價值的數學思想方法。

教師對學生的數學思想方法滲透，需要經過循序漸進和反復訓練，才能使學生有所領悟。作為教師，要明確對所教內容中蘊含的數學思想方法，在備課時要對教材從思想方法角度仔細分析，將數學思想方法教學落到實處。

參考文獻

[1]顧泠沅.數學思想方法[M].北京：中央廣播電視大學出版社，2004.

[2]張志淼.數學學習與數學思想方法[M].鄭州：鄭州大學出版社，2006.

[3]滿慧.小學數學思想方法教學的研究與實踐[D].南京：南京師范大學出版社，2011.