Schwarzschild時空中的幾何量子失協

彭小清，吳 韜，b*

（阜陽師范學院 a.物理與電子工程學院；b.量子信息技術研究中心，安徽 阜陽 236037）

Schwarzschild時空中的幾何量子失協

彭小清a，吳 韜a，b*

（阜陽師范學院 a.物理與電子工程學院；b.量子信息技術研究中心，安徽 阜陽 236037）

本文研究了在施瓦西黑洞背景下狄拉克粒子的幾何量子失協隨著霍金效應的變化規律。在霍金溫度趨于0時，所獲得的幾何量子關聯與最初態相近。然后隨著T的增加，所獲得的幾何量子關聯會單調減小。這是因為霍金效應所產生的場熱的作用，而且還發現當r偏大時，因為泡利不相容原理和費米-狄拉克統計規律共同作用使得狄拉克系統不能被完全激發，T即使趨向于無窮大，物理上可獲得的幾何量子關聯無法完全消失，這個現象與在標量場中是完全不同的。此外，我們對所有的兩體幾何量子關聯進行了研究。結果表明，當霍金溫度趨向于0時，粒子A的B1幾何量子關聯最大，粒子BⅠ和BⅡ粒子之間的幾何量子關聯幾乎一樣，且都隨著霍金溫度的增大而單調增大。

Schwarzschild黑洞；量子關聯；量子失協；量子糾纏

在量子通信和量子計算[1,2]中量子關聯被認為是一種十分重要的資源。2001年Ollivier和Zurek[3]首先提出了用量子失協度量量子關聯。此后，量子關聯吸引了越來越多的關注[4-10]，許多學者從不同的視角相繼提出了多種不同的方式度量量子關聯。例如，幾何量子失協(Geometric quantum discord，GQD)[6,7]、改進的 MID（AMID）[8,9]、負熵和測量引起的干擾（Measurement-induced dis-turbance,MID）[10]等等。

另一方面，近幾年來，Schwarzschild黑洞背景下的霍金效應作為一種時空中的量子熱效應也引起了大量的關注[11-16]。文獻[11]在施瓦西黑洞背景下研究了狄拉克粒子系統的基于最小條件熵的量子關聯演化規律。在此文獻的啟發下，本文研究了施瓦西黑洞背景下霍金效應影響的狄拉克粒子系統的幾何量子失協動力學。結果表明，當霍金溫度趨于0時，系統所獲得的幾何量子關聯與最初態接近，然后隨著霍金溫度T的增加，所獲得的幾何量子關聯會單調減小。這是因為霍金效應所產生的熱場的作用，而且還發現當r偏大時，因為泡利不相容原理和費米-狄拉克統計規律共同作用，狄拉克系統并不能被完全激發[11]，T即使趨于無窮大，物理上可獲得的幾何量子關聯也無法完全消失，這個現象與在標量場中是完全不同的。此外，隨著霍金效應的增大，可獲得的兩體幾何量子關聯迅速減小而不可獲得的兩體量子關聯卻逐漸增大，而可以獲得的幾何量子關聯之所以減小并不是因為受到黑洞的破壞，而是由于分配的區域發生了重置而造成的。

1 幾何量子關聯的數學度量

本文采用幾何量子失協作為量子關聯的度量方式，對一個兩比特X態的幾何失協一般解析表達式為[6]

對一般的兩比特X態，其密度矩陣可以表示為：

該矩陣有七個實參數，由于局域操作等價性，設ρ14和ρ23也是實數，所以此矩陣實際上有五個獨立的參數，如果選擇在Bloch分解下表示該X態，則這五個特征參數可分別表示為[17]：

當量子態ρ處于式（2）所示的X態時，它的特征參數由式（3a～3e）表示。因此，有=(0,0,x)t和T=diag{t1,t2,t3}，X態的幾何失協表示如下：

2 Schwarzschild時空中狄拉克的量子化

1916年，施瓦西提出了一種稱為施瓦西黑洞的物理模型，它設定的不帶電荷而且沒有自旋，并且黑洞的中心是奇點。本文中出現的常數諸如引力常數G、光速c、約化普朗克常量以及波爾茲曼常數都規定為一個單位，則其度規可以寫成：

其中M為黑洞質量。將該度規帶入狄拉克方程[18]

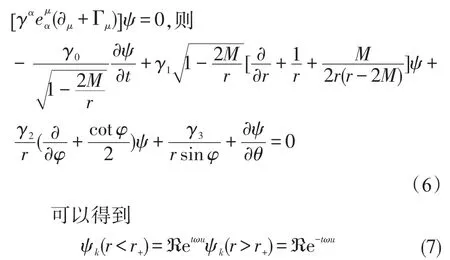
分別對應的是視界內外臨近的一組正頻費米波模[19]。其中?表示施瓦西黑洞所對應的四分量旋[20]，ω表 示 狄 拉 克 頻 率 ，μ=t-r*和r*=r+2Mln[r-2M]/2M表示烏龜遲緩坐標。波模ψk(r＜r+)和ψk(r＞r+)構成一組完備的正交基，之后對狄拉克場進行相應的量子化。

另外，引入類光 Kruskal坐標，用Damour-Ruffini方案[21]對式（7）進行解析拓展，得到 Kruskal波模。而對于Dirac場，可以采取同樣的方法將其量子化，獲得的就是Dirac場對Kruskal波模的展開。找到適當的內積，就可以得到施瓦西時空和Kruskal時空中產生算符和湮滅算符之間Bogoliubov變換[22]關系，因此,模K的 Kruskal真空態表示為：

T=1/8πM是此黑洞的霍金溫度[19]，分別代表的是視界線內外的標準的正交基，上標{+,-}則分別代表著正粒子真空和反粒子真空，同理，Kruskal唯一激發態表示為：

3 SCHWARZSCHILD黑洞背景下的幾何量子失協變化規律

考慮Alice和Bob最初共享如下形式的Werner態[23]：

Ailce用Minkowski模表示，Bob用黑洞模表示。由于黑洞視界的內外部是沒有因果關聯的，因此,對視界內的粒子Trace就行了(此處為BII粒子），根據式（8）和(9)可得到：

式中α=(e-ωk/T+1)-1/2,β=(eωk/T+1)-1/2，其矩陣形式：

由式（3a-3e）可得在Bloch分解下的五個特征參數為：

圖1 在頻率一定情況下GQD隨T的變化曲線

圖1給出了在頻率ω一定的情況下，幾何量子關聯（GQD）隨著霍金溫度（T）的變化曲線。從圖中可以發現：當T趨向于0時，可以想象此時的黑洞正在走向極端，而這個時候能夠探測到的量子失協，與剛開始的Werner態相比較，能夠發現它們的大小幾乎是相等的，并沒有十分明顯的差別。然后，隨著T的增大，因為霍金效應所產生的熱場的作用，所獲得的量子關聯會單調遞減。

此外，從圖中還可發現：當r偏大時，T即使趨向于無窮大，在物理上可獲得的幾何量子關聯也沒有辦法完全消失，此現象與在標量場中是完全不同的。這是由于泡利不相容原理和費米-狄拉克統計規律共同作用，狄拉克系統并不能被完全激發[11]。

為了進一步理解幾何量子關聯消失的原因，假設B的波模由于受到霍金效應的影響，分生了分離，分離成了BI和BII，這種變化導致了量子關聯的重新分配。所以，分別對視界外部區域的波模BI和粒子A求跡，就可以獲得ABII和BIBII的密度矩陣。

ABII的密度矩陣為：

亦即

因此，由式（3a-3e）可得在Bloch分解下的五個特征參數為：

BIBII的密度矩陣為：

亦即

因此，由式（3a-3e）可得在Bloch分解下的五個特征參數為：

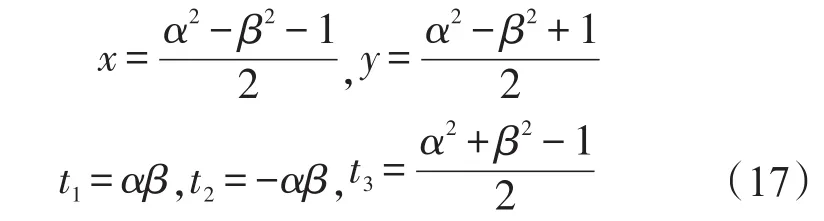
由式（17）可以觀察到：在兩個子系統之間，量子屬性與參數r是沒有關系的，因為在一開始的推導過程中，我們就已經把這種影響消除了，所以在此處不再予以考慮。在圖2中繪畫出了在r=0.9時，所有兩體幾何量子關聯隨著T升高的變化圖像。在圖中可以看出，當霍金溫度趨向于0時，粒子A和B1的幾何量子關聯最大，而粒子B和BII，粒子A和BII之間的幾何量子關聯幾乎為零，且都隨著T的升高而單調增大。當霍金效應增強時，從圖2中可以非常清晰地看到，能夠獲得的量子關聯以一個很快的速度減小，與此同時兩個不可獲得的兩體關聯卻漸漸增大。能夠獲得的量子關聯之所以減小，并不是由于它受到了黑洞的影響，而是被重新分配到了其他的區域，而在這些區域中造成了其幾何量子關聯的無法獲得。

圖2 r=0.9時兩體幾何量子關聯隨T的變化曲線

4 小結

在施瓦西黑洞背景下，討論了霍金輻射對狄拉克粒子幾何量子失協的影響。結果表明，當霍金溫度趨于0時，系統所獲得的幾何量子關聯與最初態接近，然后隨著T的增加，所獲得的幾何量子關聯會單調減小。這是因為霍金效應所產生的熱場的作用，而且還發現當r偏大時，因為泡利不相容原理和費米-狄拉克統計規律共同作用，狄拉克系統并不能被完全激發[11]，T即使趨于無窮大，物理上可獲得的幾何量子關聯也無法完全消失，這個現象與在標量場中是完全不同的。此外，隨著霍金效應的增大，可獲得的兩體幾何量子關聯迅速減小而不可獲得的兩體量子關聯卻逐漸增大，而可以獲得的幾何量子關聯之所以減小并不是因為受到黑洞的破壞，而是由于分配的區域發生了重置而造成的。

[1]Nielsen M A,Chuang I L.Quantum computation and quantum information[M].Cambridge：cambridge university press,2000.

[2]Bennett C H,DiVincenzo D P.Quantum information and computation[J].Nature,2000,404：247-255.

[3]Ollivier H,Zurek W H.Quantum discord：a measure of the quantumness of correlations[J].Physical Review Letters,2002,88(1)：017901.

[4]Celeri L C,Maziero J,Serra R M.Theoretical and experimental aspects of quantum discord and related measures[J].International Journal of Quantum Information,2011,9(7/8)：1837-1873.

[5]Modi K,Brodutch A,Cable H,et al.The classicalquantum boundary for correlations：Discord and related measures[J].Reviews of Modern Physics,2012,84(4)：1655-1707.

[6]Daki B,Vedral V,Brukner C.Necessary and sufficient condition for nonzero quantum discord[J].Physical Review Letters,2010,105(19)：190502.

[7]Luo S,Fu S.Geometric measure of quantum discord[J].Physical ReviewA,2010,82：034302.

[8]Wu S J,Poulsen U V,Molmer K.Correlations in local measurements on a quantum state,and complementarity as an explanation of nonclassicality[J].Physical ReviewA,2009,80(3)：032319.

[9]Girolami D,Paternostro M,Adesso G.Faithful nonclassicality indicators and extremal quantum correlations in two-qubit states[J].Journal of Physics AMathematical and Theoretical,2011,44(35)：352002.

[10]Luo S.Using measurement-induced disturbance to characterize correlations as classical or quantum[J].Physical ReviewA,2008,77：022301.

[11]Xu S,Song X K,Shi J D,et al.Probing the quantum correlation and Bell non-locality for Dirac particles with Hawking effect in the background of Schwarzschild black hole[J].Physics Letters B,2014,733(6)：1-5.

[12]Bak D.Entropy of universe as entanglement entropy[J].Physics Letters B,2013,721(4/5)：323-328.

[13]Eune M,Kim W.Entropy and temperatures of Nariai black hole[J].Physics Letters B,2013,723(1/3)：177-181.

[14]Flassig D,Pritzel A,Wintergerst N.Black holes and quantumness on macroscopic scales[J].Physical Review D,2013,87：084007.

[15]Bodendorfer N.Black hole entropy from loop quantum gravity in higher dimensions[J].Physics Letters B,2013,726(4/5)：887-891.

[16]Zhang B C,Cai Q Y,Zhan M S,et al.Towards experimentally testing the paradox of black hole information loss[J].Physical Review D,2013,87(4)：044006.

[17]Chen Q,Zhang C J,Yu S X,et al.Quantum discord of two-qubit X states[J].Physical Review A,2011,84(4)：042313.

[18]Brill D R,Wheeler J A.Interaction of neutrinos and gravitational fields[J].Reviews of modern physics,1957,29：465.

[19]Jing J L.Late-time behavior of massive Dirac fields in a Schwarzschild background[J].Physical Review D,2004,70(6)：065004.

[20]Wang J,Pang Q,Jing J.Projective measurements and generation of entangled Dirac particles in Schwarzschild spacetime[J].Annals of Physics,2010,325：1190.

[21]Damour T,Ruffini R.Black-hole evaporation in the Klein-Sauter-Heisenberg-Euler formalism[J].Physical Review D,1976,14(2)：332-334.

[22]Barnett S M,Radmore P M.Methods in theoretical quantum optics[M].New York：Oxford University Press,1997：67-80.

[23]Bellomo B,Lo Franco R,Compagno G.Entanglement dynamics of two Independent qubits in environments with and without memory[J].Physical Review A,2008,77(3)：032342.

Geometric quantum discord in Schwarzschild spacetime

PENG Xiao-qinga,WU Taoa,b*
(a.School of Physics and Electronics Engineering;b.Research Center of Quantum Information Technology,Fuyang Normal University,Fuyang Anhui236037,China)

In this paper,we mainly studies the effect of the Hawking radiation on the geometric quantum discord(GQD)for Dirac particles in the background of Schwarzschild black hole.It is shown that when the Hawking temperatureT→0 the quantum properties of physically accessible state are same for the initial situation.For finite Hawking temperatureT,the accessible GQD monotonously decreases along with increasingTowing to the thermal fields generated by the Hawking effect,and the accessible GQD will be disappeared when the Hawking temperature is more than a fixed value which increases with the parameterrof Werner state growing.Then we analyzed where the lost physically accessible GQD go,and found that they are redistributed to all the bipartite states.Moreover,it is found that when the Hawking temperature is infinite,corresponding to the case of the black hole evaporating completely,the GQD ofρAB1andρABⅡare identical.The inaccessible correlation between modes BⅠand BⅡ,between modesAand BⅡmonotonously increase with increasingT.

Schwarzschild black hole;quantum correlation;geometric quantum discord;quantum entanglement

O431.2

A

1004-4329（2017）03-035-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2017）03-035-05

2017-05-05

安徽省高校優秀青年人才支持計劃重點項目（gxy1ZD2016190）；阜陽師范學院教研項目（2016JXTD03，2015JYXM34）；阜陽師范學院科研創新團隊（kytd201706）資助。

吳 韜（1975- ），男，博士，教授，研究方向：量子信息。Email：wutaofuyang@126.com。