高中物理臨界問題的一點體會
孫瑞凝
(山東省肥城市泰西中學(xué)2016級16班,山東 肥城 271600)
高中物理臨界問題的一點體會
孫瑞凝
(山東省肥城市泰西中學(xué)2016級16班,山東 肥城 271600)
高中物理的臨界問題一直是高考中的熱點,在臨界問題的解決過程中,關(guān)鍵是確定臨界術(shù)語,找出臨界條件,問題就容易解決了.
高中物理;臨界值問題;平衡
在高中物理的解題過程中,分析一個物理過程轉(zhuǎn)變?yōu)榱硪粋€物理過程是經(jīng)常遇到的,也就是臨界問題.高中物理中的臨界問題一直是高考中的熱點.分析近幾年的高考的物理典型題,不難發(fā)現(xiàn)對物理過程的臨界問題考察一般是運用物理現(xiàn)象的臨界狀態(tài)分析.
在臨界問題的解決過程中,關(guān)鍵是確定臨界術(shù)語,找出臨界條件,也要能夠立足課本,確立高于課本的指導(dǎo)方針,對臨界問題的概念和計算方法理解到位,不留盲點.在物理復(fù)習(xí)中,專題的練習(xí)大部分都是課本上的例題、習(xí)題,以及例題和習(xí)題的變式,所以要能夠掌握基礎(chǔ)知識和基礎(chǔ)技能,精通課本.
對于臨界值的求法,則有兩種方法,一種是用物理規(guī)律求極值,例如,臨界條件、邊界條件等.第二種方法是用數(shù)學(xué)方法求極值,如不等式、二次函數(shù)、三角函數(shù)和解三角形等.
一、運動學(xué)和力學(xué)中常見的臨界問題
例1 一輛貨車以V0=8m/s的速度勻速行駛,經(jīng)過一輛交警車旁的時候,交警發(fā)現(xiàn)該貨車有違章行為,決定追趕并攔截,經(jīng)過2.5s,警車發(fā)動,以加速度a=2m/s2做勻加速運動,則在警車追上貨車之前,兩車之間的最大距離是多少?
分析本題考察的是速度相等的臨界條件,警車和貨車的速度相等的時候,兩車的距離是最遠的.
解由題意可知,兩車速度相等的時候,距離是最遠的得v警=at,v貨=v0,則v警=v貨,
可以得到at1=v0
則兩車相距較遠的時候,警車所用的時間為
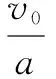
這是貨車行駛的距離為:
x貨=v0(t0+t1)=8×(2.5+4)m=52m
警車行駛的距離為:
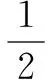
可得到兩車的距離為x貨-x警=36m
點撥運動學(xué)和力學(xué)中的臨界值問題,比較常見的是追擊和相遇問題,也就是討論兩物體運動的過程中,在相同的時間內(nèi)達到的空間的位置,以例1為例,則存在兩個關(guān)系,一個是時間關(guān)系,一個是位移關(guān)系,在做題的過程中,畫草圖也能夠得到.在該問題中,臨界條件則是兩車的速度相等,也就是能否追的上的臨界條件,也是判斷分析的切入點.
二、豎直平面內(nèi)的圓周運動的臨界值問題
例2 如圖1所示,將細繩為L,一端固定在O點,另一端系一質(zhì)量為m的小球,如果使小球在恰好豎直平面內(nèi)做圓周運動,,則小球到達最低點的速度是多少?
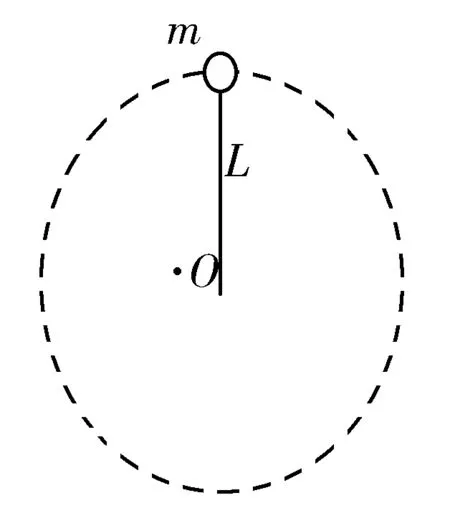
圖1
分析小球在做圓周運動的時候,其臨界最小的速度為mg=mv2/r,
解由物體做圓周運動的時候可知,當(dāng)物體達到最低點的時候,因為向心力跟重力相等
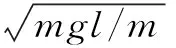
點撥在小球做圓周運動的時候,在圓形軌道中,臨界條件是一樣的,只要求出小球在受力平衡的時候受力情況,則可以求出相應(yīng)的臨界值速度.同理,在圓運動的過程中,也可以換成輕桿,則這時候臨界條件變?yōu)榱?
三、電學(xué)中常見的臨界值問題
例3 如圖2所示,在一個水平向右的勻強電場中,場強未知,在選點O上掛有一繩長為l的細繩,下端系著質(zhì)量為m,電量為+q小球,將小球拉到水平位置靜止進行釋放,當(dāng)小球擺到C點的時候,再重新擺回.當(dāng)OC與豎直方向成30°角,求小球在運動過程中的最大速度是多少?
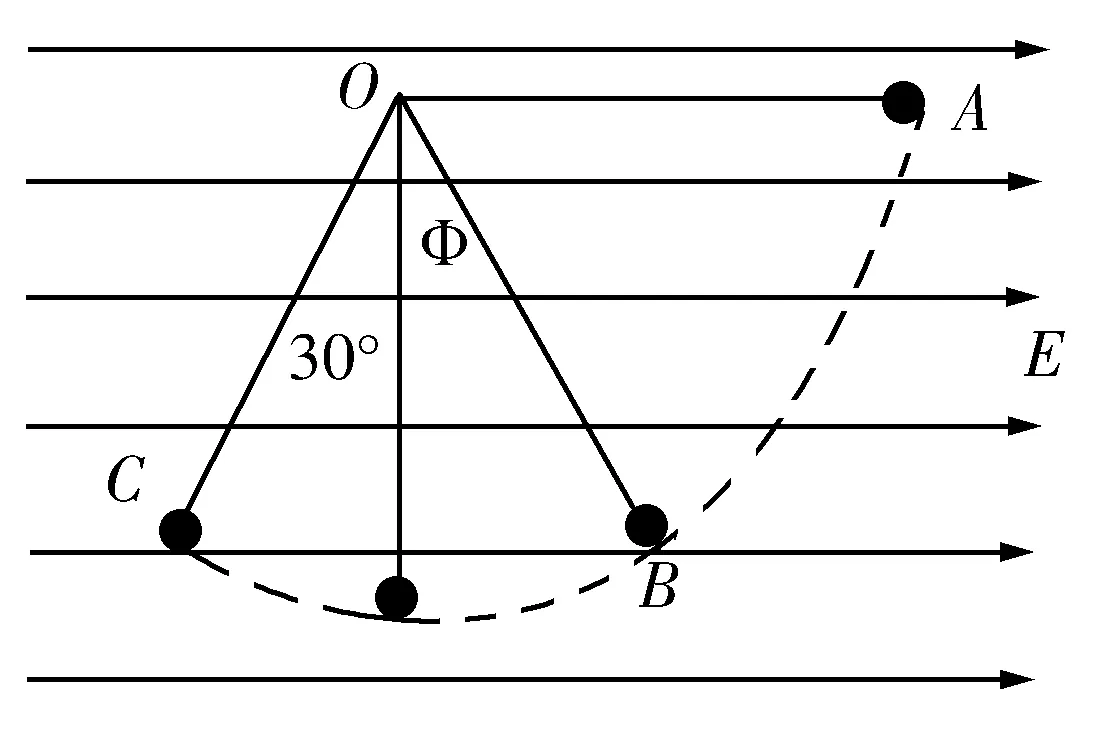
圖2
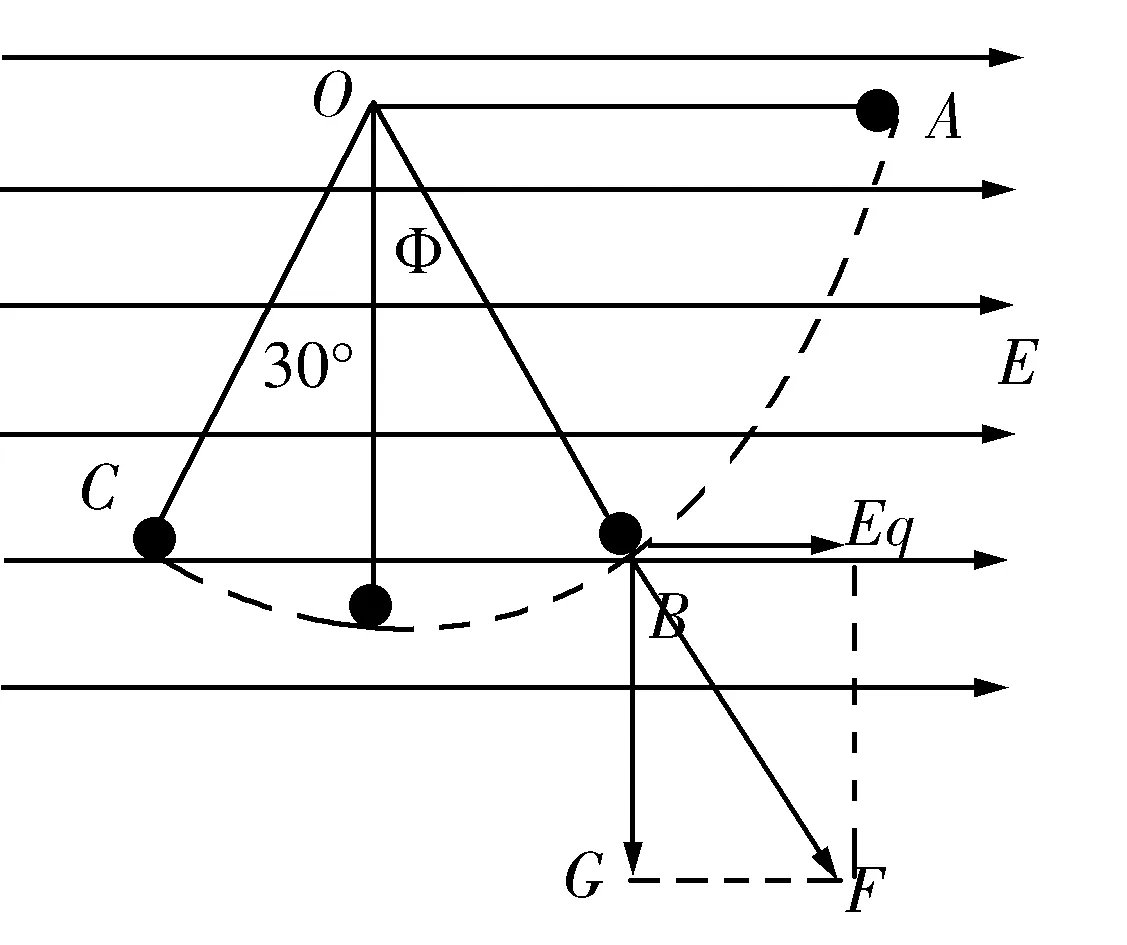
圖3
分析在該電場中,小球從A到C的運動類似單擺運動,單擺的過程中,物體到達平衡位置的時候有最大速度,也就是當(dāng)小球達到B點處于平衡,具有最大速度,這時候小球與豎直位置成φ=30°也或者是在小球運動的過程中,從A到C的運動,是在重力場和電場的復(fù)合作用下進行的,也就是在由這兩種場力組成的復(fù)合場力與小球共線,為小球的平衡位置,這時候小球有最大速度.

則可以求出
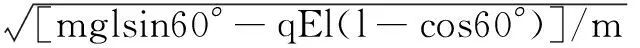
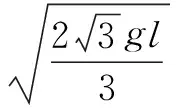
點撥在電場和重力場的綜合場的作用下進行分析,則首先要能夠找到其臨界問題的臨界條件,對臨界條件中物體的受力進行分析.在該題的解題過程中,首先要能夠意識到小球的運動類似單擺,找到單擺在靜止的過程中受力情況則可以分析出小球的臨界速度.
此外,在有關(guān)物體在質(zhì)量守恒和帶電粒子在有界磁場中的運用的過程中,牛頓運動定律的臨界值的過程中也經(jīng)常會遇到臨界值的問題.這些問題的過程中主要是通過分析物體運動的過程中所處的臨界狀態(tài)和臨界值,則可以以這個為突破口進行受力分析,使問題得以解決.
在臨界值問題中,臨界狀態(tài)的判斷和分析要能夠與平衡態(tài)和極限思維練習(xí)在一起,在給定的物理情景中求物體物理量的最大值或者是最小值,跟高等數(shù)學(xué)中國的極限值思維是相似的,所以,在解答這一類題目的過程中,首先在腦海中有有清晰的物理情景,再進行物理過程的分析,根據(jù)物體的受力情況,找到相應(yīng)的臨界值條件或者是極值的條件,解決問題,這樣也可以培養(yǎng)思維邏輯能力和分析能力.同時也要能夠夯實課本上的主要公式和定理,這樣可以熟練地運用所學(xué)知識,在分析的時候很快找到相應(yīng)的思路.
[1]聞韜. 運用臨界條件解決高中物理帶電體在磁場中運動的問題[J]. 亞太教育,2016,(04).
[2]胡俊梅. 高中物理臨界極值問題的處理方法[J]. 和田師范專科學(xué)校學(xué)報,2012,31(05).
G632
B
1008-0333(2017)22-0084-02
2017-06-01
孫瑞凝(2001.10-),女,山東肥城,高中在讀.
責(zé)任編輯:閆久毅]

