PGSA算法在船舶電網繼電保護整定中的應用
冒如權,李成陽
?
PGSA算法在船舶電網繼電保護整定中的應用
冒如權1,李成陽2
(1.海軍駐上海地區艦艇設計研究軍事代表室,上海,200011;2.武漢船用電力推進裝置研究所,武漢430064)
對于具有較大規模的船舶電網,基于設計者經驗的保護整定方法已經難以滿足需要。PGSA算法是一種特性優良的優化算法,本文通過MATLAB編寫基于PGSA算法的優化程序,對采用反時限過電流保護的某型工程船的保護整定參數進行了尋優,從而獲得了具有優良特性的保護整定參數。
PGSA算法 船舶電網 繼電保護 參數整定
0 引言
采用綜合電力推進系統的船舶電網具有電網拓撲復雜、電壓等級高、短路電流大等特征。當船舶電網出現短路等故障時,繼電保護系統應能滿足可靠性、速動性、選擇性和靈敏性的要求,快速切斷故障支路,防止故障擴大,保證船舶電網的穩定可靠運行。隨著船舶電網規模的日益復雜,基于經驗的繼電保護整定方法已經難以滿足需要,因此有必要借鑒陸上電網的整定方法,通過某種優化算法對船舶繼電保護的整定值進行尋優,以期獲得具有更加優良特性的整定結果。PGSA(模擬植物生長)算法,是一種模擬植物生長過程的智能優化算法。本文根據PGSA算法原理,在MATLAB中編寫優化算法模塊,對采用反時限過電流保護的某型工程船船舶電網的保護進行整定。
1 PGSA算法原理
目前已有的智能優化算法原理大多數來自于人類對自然和社會的觀察和模擬,PGSA算法是其中一種較為優秀的仿生優化算法。該算法借鑒植物向光性原理,通過模擬植物在自然環境中枝葉生長的過程,最終獲得目標函數的最優解。植物的生長過程主要受到體內生長素分布的影響,生長素越高的地方,植物生長出枝條的可能性越大。植物受到較強陽光照射的部位,生長素的濃度較高。這些部位獲得優先生長的機會,因此整個植株不斷向陽光方向生長。假設有一株植物在一個受到約束條件限制的n維空間里生長,定義空間位置向量X=(1,2,…n)。定義()為背光函數,背光函數反應了光照在生長空間中分布,若背光函數()越大,表示該位置的光照強度越低。將植物形狀簡化為三個部分,分別為根、樹干和樹枝。記假定植物根的初始生長位置為0,按照約定步長在樹干上尋找到比根光照強度更大的位置,這些位置被稱為生長點。樹干上生長點的數量為,那么生長點的空間坐標向量stem=(stem1,stem2, …stemK)。用向量stem=(stem1,stem2, …stemK)表示在這些生長點處的生長素的濃度,該向量可以通過公式(1)進行計算:
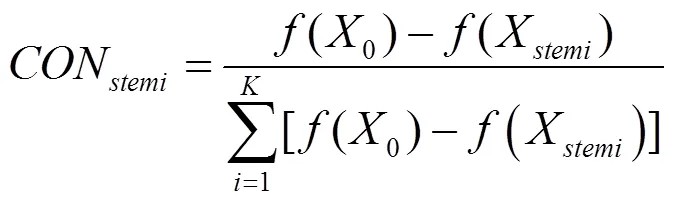
圖 1生長素狀態空間
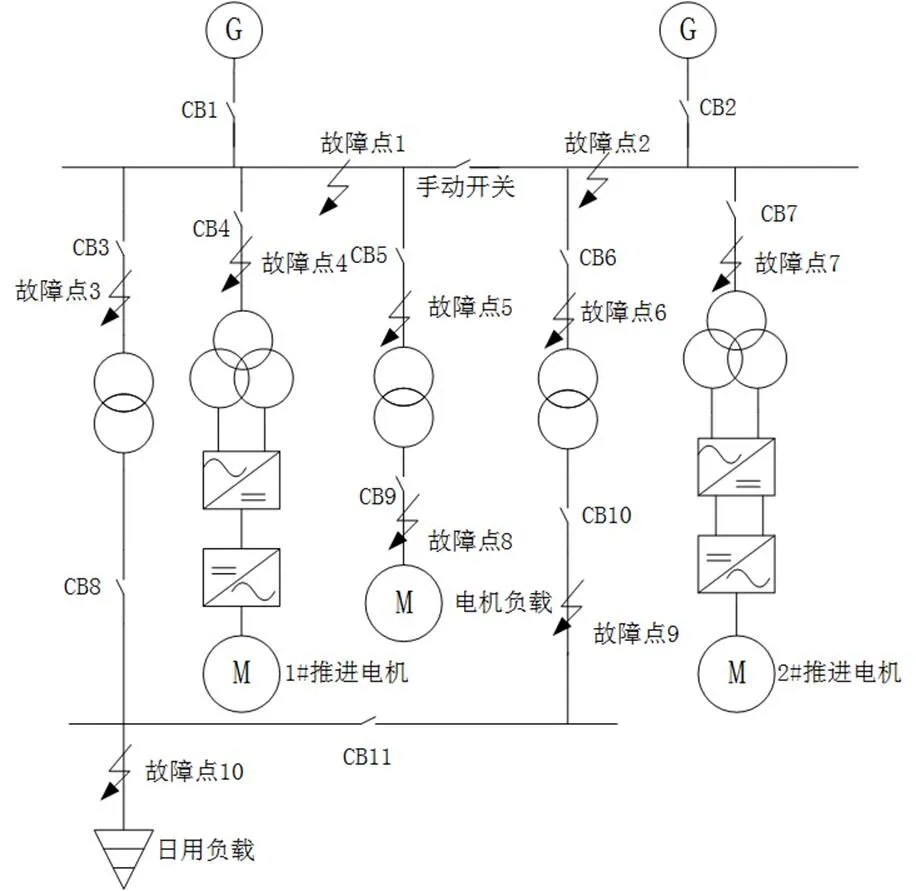
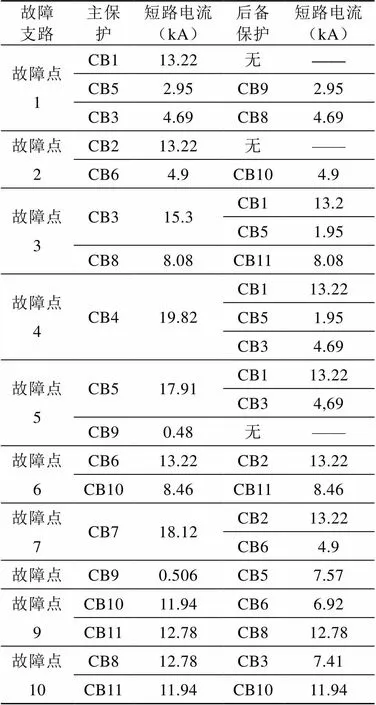
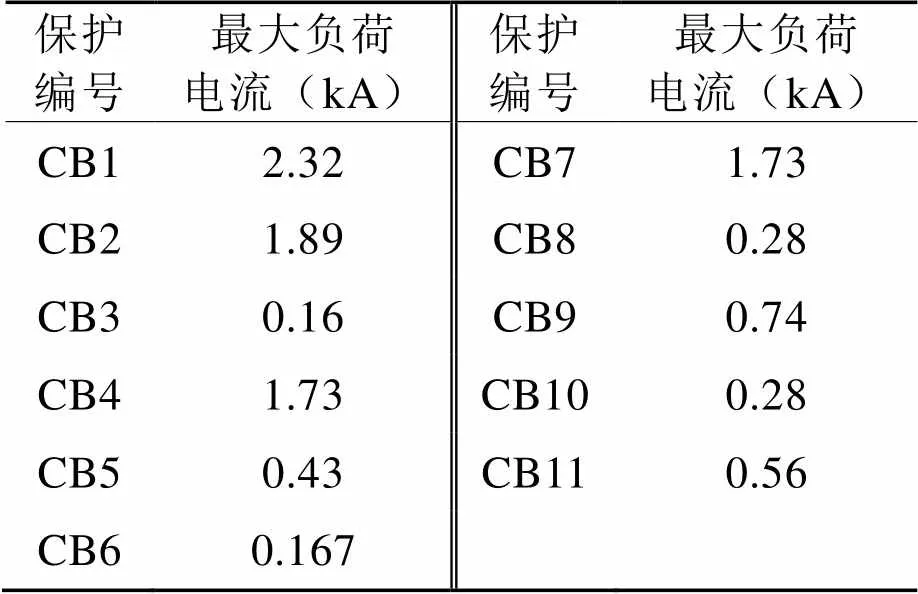
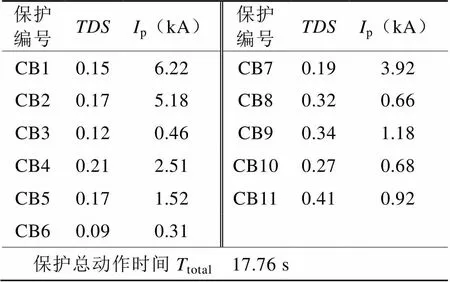
若隨機數P滿足{stemi≤ 此時生長點集合中共有+個生長點,根據公式(2)可得,所有生長點的生長素分布濃度之和滿足方程(3): (3) 再次通過計算機產生[0,1]中隨機數,通過P落入狀態空間的位置確定下一個樹枝的生長點。重復上述過程,植物將不斷并生長出新的樹枝,直到樹枝長滿所有的生長空間,已經無法找到新的生長點為止。此時可以認為已經尋找到了最優解,即最后一個生長樹枝的起始點。PGSA算法優點在于該算法將目標函數和約束條件分開處理,不需要構造新的目標函數,并且原理較為簡潔,易于使用計算機對算法進行實現[1]。 保護整定的目標是保護能夠在滿足選擇性、可靠性和靈敏性的前提下,當電網出現故障時,故障支路的主保護能夠盡快動作,保護整體動作時限最短[2]。 反時限過電流保護的特點是保護時限隨著過電流增大減小,通過時間級差來保證主后備保護的選擇性。與三段式定時限過電流保護相比,反時限過電流保護能夠更快的切除故障,并且實現反時限過電流保護的設備成本更低,適合應用于船舶電網。基于IEEE/ANSI規定的通用的反時限過電流保護的電流-時間動作特性曲線為[3]: 其中為保護動作時限,為繼電器中流過的過電流,1、2、3是反時限保護系數,為時間常數,p為保護繼電器中的啟動電流。若≤I,那么時間為負,表示流過保護短路電流未達到保護的啟動電流,那么反時限保護將不工作。只有當I時,時限為正,反時限過流保護才能工作。按照IEC推薦的標準反時限保護模型,取3=0,1=0.14,2=0.02。標準反時限過電流保護時間曲線為: (5) 若電力系統共計有條支路,當第條支路發生故障時,該支路的主保護動作,保護的動作時限為t,那么保護的目標函數為: 上式中w稱為權重系數,反映了線路負載的重要性。由于船舶電力系統規模較小,為了簡化分析,故取w=1。將式(5)帶入式(6)中,可得反時限過電流保護的目標函數: (7) 式中TDS保護的時間常數,pk時保護的啟動電流,I是支路故障時流經保護的短路過電流。由式(7)可知,目標函數f是反時限過電流保護的整定系數TDS和啟動電流I的函數。因此整定的優化變量為k和啟動電流pk。同時,反時限過電流保護的整定系數和啟動電流I需滿足一定的約束條件。 首先保護的參數需要在一定范圍內進行整定。保護的時間常數和啟動電流需要滿足上下限的約束。時間常數的上下限由保護的特性決定。為了滿足保護的可靠性,保護的啟動電流I的下限為最大負荷電流Imax乘以系數1,保證保護在正常運行狀態下不發生誤動。為了滿足保護的靈敏性,保護的啟動電流I的上限為所有短路情況中的最小短路電流Imin乘以系數2,保證保護故障情況下不發生誤動。上述約束條件可用式(8)和式(9)表達: (9) 同時,相鄰的保護需要滿足選擇性,若支路發生故障,那么支路的主保護應優先于后備保護的動作,因此在主保護和后備保護的時限需要滿足一定的時間級差,即滿足方程(10): t表示主保護的保護時限,t表示保護的保護時限。對于微機保護,考慮到斷路器跳閘時間、計算誤差以及時間繼電器的誤差等因素,一般誤差不小于0.2 s[4]。 以某型裝備電力推進系統的工程船為例,將PGSA算法應用于該船電網的反時限過電流保護參數的整定中。工程船電網的拓撲結構如圖2所示,為了簡化分析,將部分發電機組及其支路進行了合并。其中發電機的控制系統中已經配置過電流保護,為了保證系統支路出現故障時,船舶能夠可靠保證單側運行,因此變壓器原邊側母線手動開關在故障發生時為開路狀態。整個系統中未添加電流方向判斷元件。變頻器的控制器中包括了過電流保護功能,因此推進電機支路不考慮負載電動機向短路點的回饋電流。電網中共計有10個故障節點,所有斷路器均配置反時限過電流保護。 圖2工程船電網拓撲圖 在工程船的電力系統中,通過ETAP電網計算軟件對流過保護支路的主后備保護對的短路電流計算,結果如表1所示。 表1工程船電網短路電流 故障支路主保護短路電流(kA)后備保護短路電流(kA) 故障點1CB113.22無—— CB52.95CB92.95 CB34.69CB84.69 故障點2CB213.22無—— CB64.9CB104.9 故障點3CB315.3CB113.2 CB51.95 CB88.08CB118.08 故障點4CB419.82CB113.22 CB51.95 CB34.69 故障點5CB517.91CB113.22 CB34,69 CB90.48無—— 故障點6CB613.22CB213.22 CB108.46CB118.46 故障點7CB718.12CB213.22 CB64.9 故障點8CB90.506CB57.57 故障點9CB1011.94CB66.92 CB1112.78CB812.78 故障點10CB812.78CB37.41 CB1111.94CB1011.94 對流過保護的最大負荷電流進行計算,計算結果如表2所示。 表2流過保護的最大負荷電流 保護編號最大負荷電流(kA)保護編號最大負荷電流(kA) CB12.32CB71.73 CB21.89CB80.28 CB30.16CB90.74 CB41.73CB100.28 CB50.43CB110.56 CB60.167 時間系數的取值范圍為0.05< TDS < 0.5,啟動電流I的取值范圍的上下限系數1=2=1。若主后備保護的時間級差為常數,容易出現找不到滿足約束條件的最優解的情況,考慮保護的動作誤差和系統擾動的影響,主后備保護的時間級差0.2 s < Δ<10 s。在MATLAB中編寫PGSA優化算法模塊,將優化計算的目標函數和約束條件輸入到PGSA優化算法模塊中完成整定計算。整定結果如表3所示。 表3反時限過電流保護的整定結果 保護編號TDSIp(kA)保護編號TDSIp(kA) CB10.156.22CB70.193.92 CB20.175.18CB80.320.66 CB30.120.46CB90.341.18 CB40.212.51CB100.270.68 CB50.171.52CB110.410.92 CB60.090.31 保護總動作時間Ttotal 17.76 s17.76 s 在整定完成后,需要對整定結果進行選擇性校驗。以故障點1為例,當故障點1處發生短路時,需要動作的保護的時限如表4所示。 表4 動作的保護時限 主保護動作時限(s)后備保護動作時限(s) CB11.12———— CB51.82CB94.56 CB30.66CB80.94 圖3 故障點1反時限保護曲線圖 從整定結果來看,當故障點1故障時,如圖3所示,主保護CB5和后備保護CB9以及主保護CB3和后備保護CB8之間能夠較好的滿足配合性,同時能夠整定參數結果能夠式(8)和式(9)規定的上下限的約束條件。 陸上電網在完成繼電保護的整定后,需要修正主后備保護的整定曲線可能存在交叉問題,比如在圖3中主保護CB3和后備保護CB8的曲線出現了交叉。對于陸上電網,當出現近端故障時,短路電流較大,保護的配合關系正確,隨著故障點遠離電源點,短路電流減小,后備保護可能先于主保護動作,保護間失去選擇性[4]。但是由于船舶電力線路較短,線路阻抗小,故障發生在支路近端和故障發生于支路遠端的短路電流幾乎完全一樣,因此故障點的在支路上的位置差異不會造成后備保護先于主保護跳閘,從而造成電網故障時保護喪失選擇性問題。但是若反時限過電流保護需要能夠在單相接地故障時正確動作,那么需要通過單相接地短路電流作為參數整定的依據,將短路交叉點提前,防止出現保護失配的故障。 [1] 徐自勉. 基于樹木枝梢生長分枝過程的算法[D]. 江西理工大學, 2016. [2] 丁明, 張維, 李生虎. 反時限方向過電流保護最優協調整定分析[J]. 安徽電力, 2009, 29(1): 36-40. [3] 嚴琪, 肖萬芳. 反時限電流保護整定計算相關問題研究[J]. 電力自動化設備, 2008, 28(7): 77-80. [4] 韋嘉, 柏瑜. 反時限過流保護模型和曲線交叉研究[J]. 電測與儀表, 2015, 52(9): 59-60. [5] 侯計兵. 電力系統反時限過電流保護優化整定計算的研究[D]. 華中科技大學, 2011. Application of PGSA Algorithm in Ship Grid Relay Protection Coordination Mao Ruquan1,Li Chengyang2 (1.Representatives Office of Naval Warship Design & Research, Shanghai 200011, China;2. Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China) TM77 A 1003-4862(2017)08-0060-04 2017-06-13 冒如權(1979-),男,工程師。研究方向:艦船電氣及自動化。Email: maoruquan@163.com
2 反時限過電流保護的整定模型

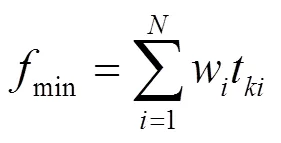
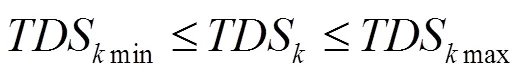
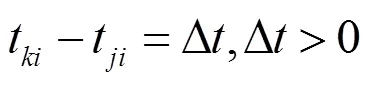
3 船舶電網繼電保護反時限過電流保護的整定