一道圓錐曲線試題的命制與分析

福建省泉州奕聰中學 (362000)

吳 鵬

福建省泉州市第五中學 (362000)

楊蒼洲

一道圓錐曲線試題的命制與分析

福建省泉州奕聰中學 (362000)

吳 鵬

福建省泉州市第五中學 (362000)

楊蒼洲

1 試題內容

設圓F1：x2+y2+4x=0的圓心為F1，直線l過點F2(2,0)且不與x軸、y軸垂直，l交圓F1于C,D兩點，過F2作F1C的平行線交F1D于點E．

(1)證明||EF1|-|EF2||為定值，并寫出點E的軌跡方程；

(2)設點E的軌跡為曲線Γ，直線l交Γ于M,N兩點，過F2且與l垂直的直線與圓F1交于P,Q兩點，記△PQM，△PQN的面積分別為S1,S2，求S1+S2的取值范圍．

2 考查目標

本題主要考查初中平面幾何知識(平行線性質、垂直平分線性質等)，直線的斜率，直線的方程，軌跡及軌跡方程，圓的方程及其幾何性質，雙曲線的定義，雙曲線的標準方程及其幾何性質，直線與圓錐曲線的位置關系，函數的最值問題等基礎知識；考查推理論證能力、運算求解能力，考查數形結合思想、函數與方程思想、化歸與轉化思想等．

3 命制過程

命題者構造了兩個定點，即圓心F1(-2,0)和F2(2,0)，動點E滿足||EF1|-|EF2||為定值，即E點的軌跡是以F1，F2為焦點的雙曲線.母題可見于《人教A版選修2-1》第62頁A組第5題.于是命題者設置了問題(Ⅰ)：證明||EF1|-|EF2||為定值，并寫出點E的軌跡方程．

為進一步突出解析幾何的基本思想方法，第二問中引入了直線、圓、雙曲線、直線與直線的位置關系、直線和圓的位置關系、直線與圓錐曲線的位置關系等大部分解析幾何的知識，以考查學生解析幾何的基本思想方法與運算求解能力、推理論證能力、轉化與化歸能力等，因此設置了問題(Ⅱ)：設點E的軌跡為曲線Γ，直線l交Γ于M,N兩點，過F2且與l垂直的直線與圓F1交于P,Q兩點，記△PQM，△PQN的面積分別為S1,S2，求S1+S2的取值范圍．

4 解題思路

第(Ⅰ)步的求解：先用圓的幾何性質求證

||EF1|-|EF2||為定值，再由定義得到雙曲線的軌跡方程．

第(Ⅱ)步的求解：設直線l:y=k(x-2)(k≠0)，然后再用弦長公式分別求出直線與雙曲線相交所得的弦長，直線與圓相交所得的弦長，從而求出△PQM，△PQN的面積，并利用函數求值域的方法求出S1+S2的取值范圍．

5 試題詳解

(Ⅰ)圓F1：(x+2)2+y2=4，圓心F1(-2,0)，半徑r=2，如圖1所示．

因為F1C∥EF2，所以∠F1CD=∠EF2D.又因為F1D=F1C，所以∠F1CD=∠F1DC，所以∠EF2D=∠EDF2，所以ED=EF2，故||EF1|-

|EF2||=||EF1|-|ED||=2<|F1F2|.

圖1

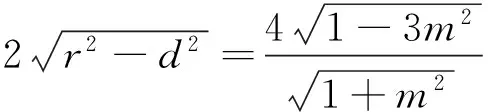
6 試題評價

本題主要檢測的數學學科素養有：運算求解能力，推理論證能力、數據圖像處理能力和知識應用意識.預計本題難度系數0.3，擬作為高考理科數學模擬試卷的第20題.

命題者呈獻給考生的是一個圓錐曲線試題.試題與全國卷圓錐曲線題型風格極其類似，適合作為參加全國卷考試的考生作為臨考的模擬考試.

(1)試題的表述簡潔明了，設問方式干凈利落，有效減少了考生的閱讀負擔.試題的母題可見于《人教A版選修2-1》第62頁A組第5題，背景熟悉，讓學生有一種似曾相識的感覺，這對身處考場的學生來說是很好的精神安慰，有利于學生水平的正常發揮.

(2)切入點多，第一問求定值可用初中平面幾何知識求解，也可用解析法；第二問求弦長，也有較多的切入點，有助于學生各顯神通，給不同層次的學生都提供了機會，對水平高的學生來說可考察知識面的寬度、解題技巧的高明、思維的深度.

(3)試題第(Ⅱ)步，考察過定點的直線與雙曲線、圓相交所成的弦長公式，通過轉化與化歸，函數的最值，重在考查學生數形結合、化歸與轉化、分類與整合的數學思想.此步驟具有明顯的區分度，能有效地區分出優等生與中等生對數學知識不同的掌握程度.

從試題及其解答可以看出本題符合考試大綱對高中畢業生的檢測要求，突出了解析幾何的基本思想方法，從試題的命題過程可以看出命題者有較高的數學素養.