大場景下多目立體視覺標定方法的研究

楚圣輝，張慧萌，陳碩，孟浩，劉國忠

（北京信息科技大學，北京 100192）

大場景下多目立體視覺標定方法的研究

楚圣輝，張慧萌，陳碩，孟浩，劉國忠

（北京信息科技大學，北京 100192）

相機的標定是機器視覺中三維重建的關鍵步驟，其精度也決定三維重建的準確性，為了解決三維重建信息不完整和大視場標定，提出一種多目相機標定的方法。它區別于傳統雙目相機標定，能夠應用于較大視場下，并且通過多個視角，提供比較全面的三維信息。采用張正友標定算法，利用黑白相間棋盤格作為標定靶標，首先通過在四個方向的四臺相機對場景中靶標進行拍攝，求出每個相機的內外參數，然后通過相機之間的矩陣關系和LM優化算法統一相機坐標系，完成多目相機系統的標定，這種方法能夠適用于大場景中，獲得完整的三維信息。最后通過實驗，給出實驗數據驗證此方法的正確性，并提出相機位置與標定精度的關系，此方法可應用于電力培訓的人體動作捕捉系統等大視場立體視覺的系統標定中，為電力培訓方法提供新思路。

大場景；多目標定；張正友標定算法；棋盤格

0 引言

近年來，人體運動捕捉技術[2]已越來越成熟，被應用在影視制作、智能監控、游戲制作、運動分析等領域。電力安全生產涉及到職工的生命安全，也影響電力系統安全、穩定的運行。由于電力系統的特殊性,對工作人員的要求也越來越高，現場的電力培訓雖然效果良好，但由于設備帶電運行，存在很多危險性和不確定性，在現場進行人員培訓具有非常大的局性，動作捕捉技術可以通過識別操作人員的位置和動作，模擬真實的操作環境，并且記錄操作流暢，可以使操作更加規范化。

相機的標定是動作捕捉系統的關鍵，在識別人體動作的過程中，為了確定相機拍攝圖像和實際空間之間的關系，必須要建立相機成像的幾何模型，這個模型的參數就是相機的內外參數，標定的過程就是確定這些參數的過程[1]。

相機的標定可以分為三類：傳統標定[3]、自標定[4]和主動視覺標定法，張正友標定法[5]，是介于傳統標定方法和自標定方法之間，使用黑白相間的棋盤格作為標定物。傳統棋盤格標定法采用兩臺相機同時對靶標進行拍攝，視場范圍相對較小，無法對空間中完整的人體活動進行捕捉，而且兩臺相機從不同角度拍攝，對部分三維信息造成丟失，重建結果不夠完整。

本文使用張正友標定法進行相機的標定，首先運用張正友標定法對四個相機依次進行標定，求出每個相機的內外參數，然后通過矩陣旋轉關系和LM優化算法，統一四個相機的坐標系完成多目相機系統的標定，可適用于較大場景中，建立比較完整的三維信息，并應用于電力培訓的人體動態捕捉中。

1 相機成像模型

在計算機視覺中，為了獲得空間中點的位置，需要通過空間中物體點與相機平面及圖像上的點對進行描述。為了方便描述，需要定義幾種坐標系：圖像物理坐標系，圖像像素坐標系，相機坐標系，世界坐標系[6]。

如圖1，以圖像左上角為O0原點建立像素為單位的圖像像素坐標系u-v，（u,v）代表像素的行和列，x-y表示圖像物理坐標系，（u0,v0）代表原點O1，

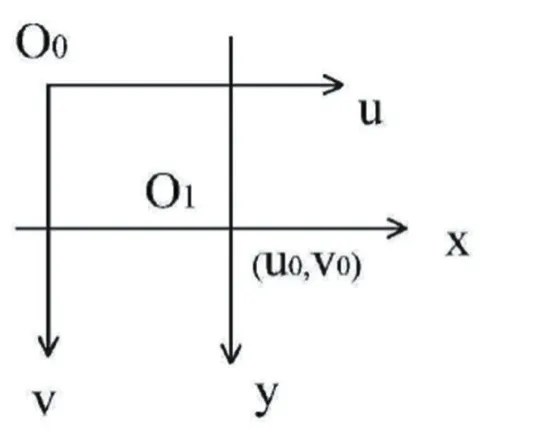
圖1 圖像物理坐標系和像素坐標系

dx和dy分別為每個像素在橫軸x和縱軸y上的物理尺寸，u-v坐標系中的坐標和x-y坐標系下的坐標關系如下：

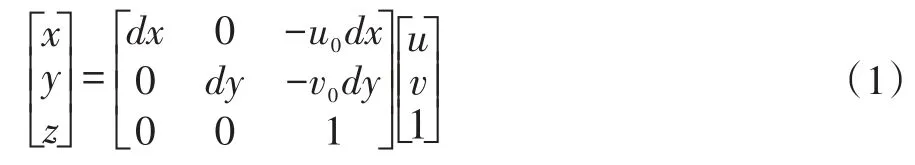
相機成像的幾何關系如圖2所示，Pw（Xw，Yw，Zw）為空間某一點P的世界坐標，PC（Xc,Yc,Zc）為該點在相機坐標系中的坐標

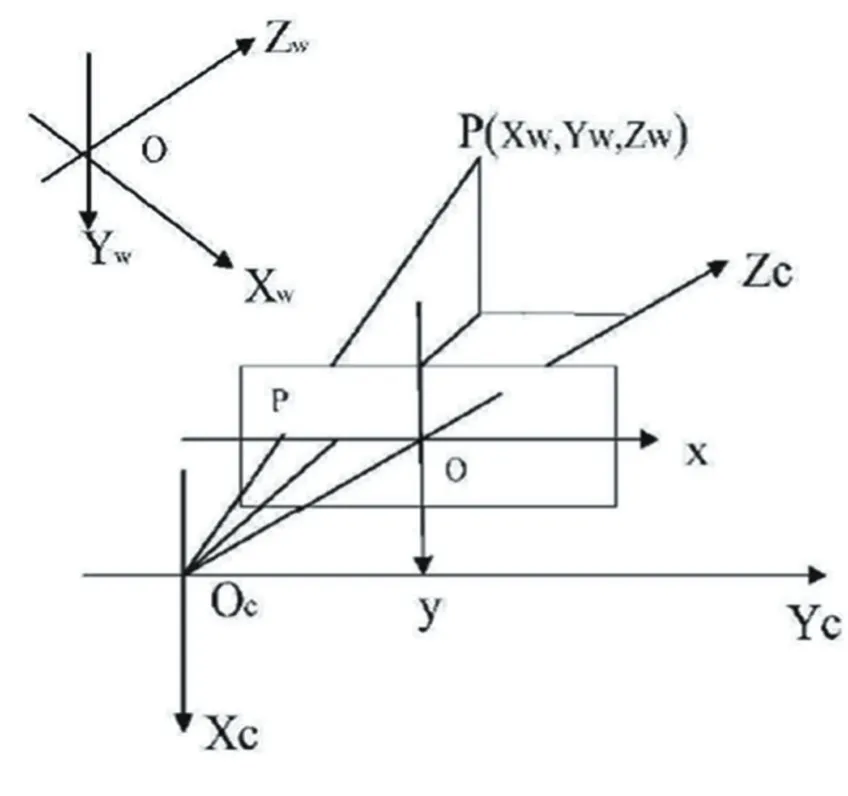
圖2 相機坐標系與世界坐標系

相機坐標系和世界坐標系的關系可用旋轉矩陣R和平移向量t描述

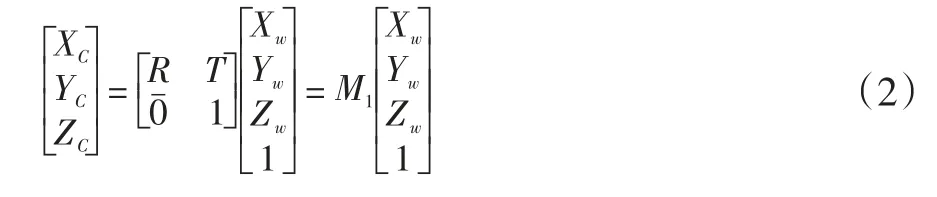
上式（2）中：R為3x3正交單位陣（也稱為旋轉矩陣）；t為三維平移向量。

根據針孔成像模型，利用三角形相似原理，得到相機坐標系和圖像坐標系的關系，用齊次坐標與矩陣的形式表示為：

式（3）中f為相機焦距。

將式（1）、（2）帶入式（3），就可以得到P的世界坐標與像素坐標的關系，如下式

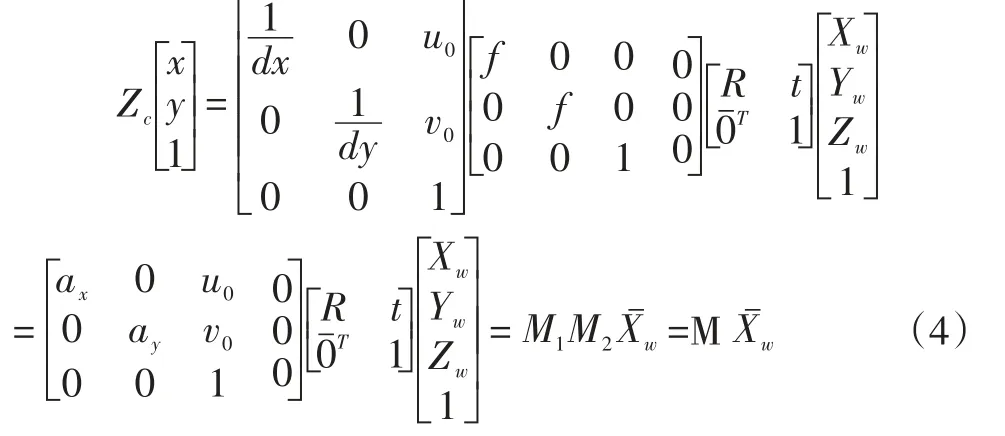
其中ax=f/dx，ay=f/dy，M1是相機的內部參數矩陣，由相機的內參數ax、ay、u0、v0所決定，M2是相機的外部參數矩陣，由旋轉矩陣R和平移向量t所決定。

2 畸變矯正

在實際成像中，考慮到鏡頭工藝等原因，一半都會存在畸變，畸變主要包括徑向畸變和切向畸變[7-8]。

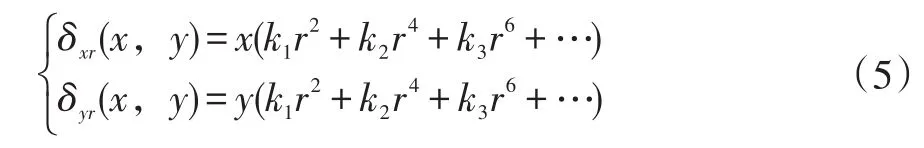
（5）式中：r2=x2+y2,k1,k2,…為相機的徑向畸變參數。

切向畸變δxt、δyt表示為：

式（6）中，p1、p2為相機切向畸變參數。

考慮相機畸變后，P點在歸一化相機物理坐標(xd, yd)表示為：

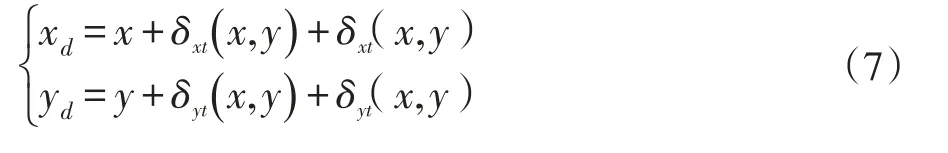
由透視變換轉化為像素坐標系下坐標（u，v）：

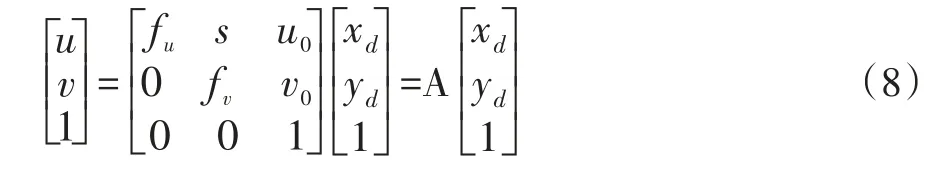
式（8）中，fu、fv為u、v兩方向歸一化焦距，s為坐標軸傾斜因子，u0、v0為主點像素坐標。

由式（5）～（8）可以求出相機內部參數 fu、fv、s、u0、v0，還有畸變系數k1,k2、p1、p2。

3 多相機坐標系統一

得到相機的內外參數之后，需要把所有的相機關聯起來，即確定相機外參數間的關系，先要確定一個統一的世界坐標系，一般以某一相機的相機坐標系為統一坐標系，然后求出每一個相機相對這個統一坐標系的旋轉關系，然后用旋轉關系求相機的平移[9]，最后用LM算法得到最優解。

圖3 相機標定示意圖

世界坐標系中任意一點坐標為W，在第i個和第j個相機坐標系中坐標分別為xi、xj，從世界坐標系到相機坐標系的轉換為：

（9）式中消去W，得到xi和xj之間的轉換關系：

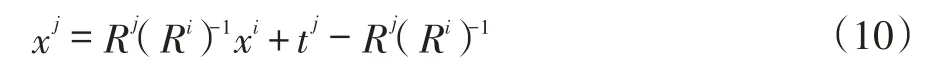
記[R t]=[R （jRi）-1tj-R（jRi）-1]，則式（10）可簡寫為xj=Rxi+t，所以，兩個相機間的選對旋轉為R= R（jRi）-1，平移向量t=tj-Rj(Ri)-1，通過標定，求出所有相機外部參數Ri、ti、Rj、tj，可以得出每個相機在統一坐標系下的關系。

4 標定結果

試驗中使用了四個CCD相機，像素尺寸為5.6μm* 5.6μm，為保證視場范圍，采用了4mm鏡頭，采用黑白相間的棋盤格作為標定靶標，提取棋盤格上角點信息進行相機的標定。對空間中靶標進行了拍攝：

圖4 標定棋盤格

試驗中為保證相機標定的精度，將棋盤格靶標在相機視場內擺放若干位置，分別拍攝了100張不同角度和位置的圖像，如圖5所示：

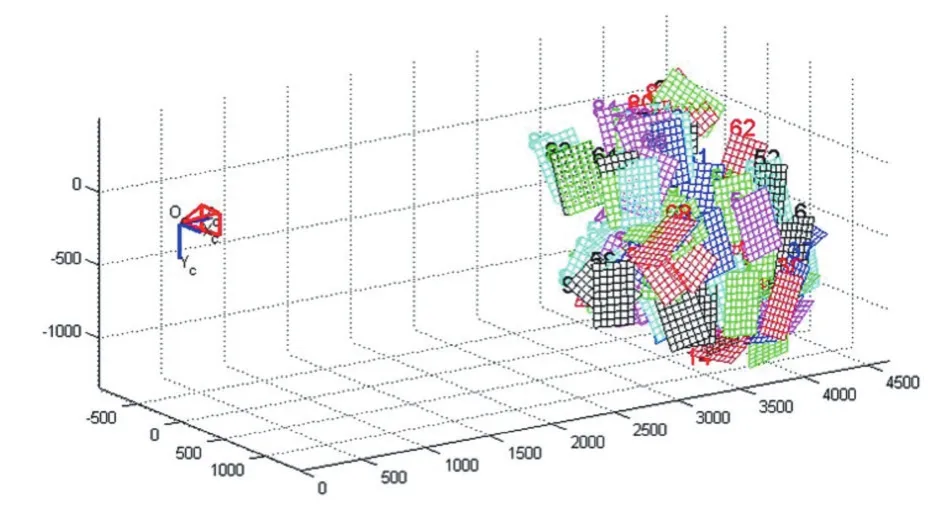
圖5 相機和靶標相對位置關系

四個相機的標定結果為：

1號相機焦距 f1=735.70553，主點坐標 c1= [332.83706，237.34153]，徑向畸變為，k11=-0.09698，k12=0.09186，切向畸變為 p11=-0.00296，p12= 0.00008。

2號相機焦距 f2=734.34412，主點坐標 c2= [348.33989，235.97910]，徑向畸變為，k21=-0.09378，k22=0.06665，切向畸變為 p21=-0.00190，p22= 0.00296。

3號相機焦距 f3=736.95946，主點坐標 c3= [341.89395，252.66362]，徑向畸變為，k31=-0.09217，k32=0.01289，切向畸變為 p31=-0.00061，p32= 0.00334。

4號相機焦距 f4=735.48787，主點坐標 c4= [334.43309,233.13859]，徑向畸變為，k41=-0.10568，k42=0.16539，切向畸變為 p41=-0.00211，p42= 0.00279。

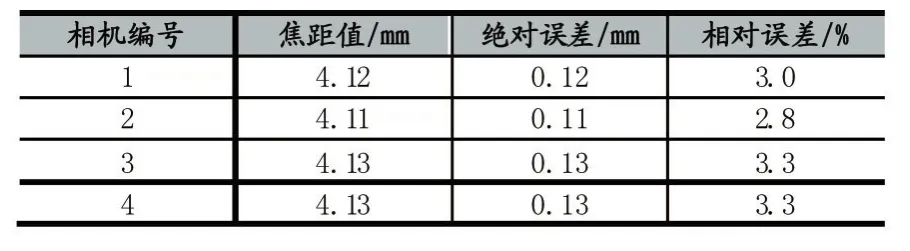
表1 相機焦距和誤差

5 測量結果與分析

利用標定結果對實際空間中兩個固定距離的小圓球進行了測量，如圖6。

首先根據圖像中點的位置，得到兩個點的像素坐標，然后根據標定的相機內外參數，求得兩點在空間中的世界坐標，計算距離[10]，最后與空間中兩點的實際距離作比較，兩小球的距離為500mm（如表2）。

列舉幾個通過相機間內外參求得的兩點空間距離（如表3）。

由表2和表3可知，在上述原理的基礎上通過拍攝圖像進行了實驗，根據實驗數據，相鄰相機間求得兩點間距離精度較高，魯棒性較好，由于實際場景中相機擺放的位置呈一個長方形，2號和3號相機、1號和4號相機之間的距離明顯長于1號和2號相機、3號和4號相機之間的距離，對應的2和3號相機、1和4號相機光軸與靶標平面所成的角度相對較大，所以坐標系統一后，誤差相對較大。由于實驗設備有限，采用了四臺相機，后期可以在2號和3號、1號和4號相機之間增加兩臺相機，減少相機間的距離，進而減小相機與靶標所成角度來增加標定精度。

圖6 空間中點位置

表2 兩個球中心圖像坐標

表3 兩球中心世界坐標

進一步實驗，在四個區域內隨意放置兩個小球點，但是固定他們中心之間的距離為300mm，如圖7所示：

圖7 兩個相機中四個區域

用兩個相機分別對每個區域拍攝十組照片，1號區域為兩個相機的圖像中心，2、3和4號區域為圖像的邊緣，與相機光軸角度較大。

表4 兩球在四個區域距離及誤差

由表4可知，2、3和4號區域相對于1號區域誤差較大，所以每個相機擺放的位置應盡量使人位于圖像的中心，減小與相機光軸所成的角度，以提高后期三維重建和人體動態捕捉的精度。

6 結語

相機的標定是機器視覺和三維重建的基礎，為機器視覺相關技術在眾多領域的應用提供了前提條件，本文在張正友標定法的基礎上，提出了一種多目相機標定，運用黑白相間棋盤格對四個相機依次進行標定，求出每個相機的內外參數，然后通過矩陣變換和LM算法優化數據，統一四個相機的坐標系完成多目相機系統的標定。提出了相機位置與標定精度的關系，在大場景下通過增加相機個數，減小相機光軸與靶標平面之間角度來減小誤差，提高標定精度，本方法用于電力系統培訓中的大視場情況下的人體動作捕捉，滿足人體在場景中位置變化的精度，為電力培訓的方法提供了新的思路。

[1]向澤銳，支錦亦，徐伯初，等．運動捕捉技術及其應用研究綜述[J]．計算機應用研究，2013，30(8)：2241-2245.

[2]馬頌德，張正友．計算機視覺:計算理論與算法基礎［M］.北京:科學出版社，1998.

[3]Tsai R．A Versatile Camera Calibration Technique fFor High-accuracy 3D Machine Vision Metrology Using Off-the-shelf Tv Cameras and Lenses[J]．IEEE Journal on Robotics and Automation，1987，3(4)：323-344．

[4]吳福超，胡占義.攝像機自標定的線性理論與算法[J].計算機學報2001，24（11）：1121-1235．

[5]Zhang Z．A Flexible New Technique for Camera Calibration[J]．IEEE Transactions on Pattern Analysis&Machine Intelligence，2000，22(11)：1330-1334．

[6]馬頌德.計算機視覺：計算理論與算法基礎[M].科學出版社，1998．

[7]Hsieh C H，Chen F C.General Two-stage Kalman Filters[J]．IEEE Transactions on Automatic Control，2000，45(4)：819-824．

[8]Zhang Z．Flexible Camera Calibration by Viewing a Plane from Unknown Orientations[C].iccv．IEEE Computer Society,，1999:666．

[9]Martinec D，Pajdla T．Robust Rotation and Translation Estimation in Multiview Reconstruction[C].IEEE Conference on Computer Vision and Pattern Recognition．IEEE，2007:1-8．

[10]Faugeras O.Three-dimensional Computer Vision:A Geometric Viewpoint[M].Springer-Verlag，1987．

Research of Multi-view Calibration in Wide Field

CHU Sheng-hui，ZHANG Hui-meng，CHENG Shuo，MENG Hao，LIU Guo-zhong

（Beijing Information Science and Technology University,Beijing 100192）

Camera calibration is the key step in the machine vision and three-dimensional reconstruction,Its precision is also determines the accura?cy of the three-dimensional reconstruction,this paper presents a method of multi-camera calibration in order to solve the wide field calibra?tion and incomplete information of three-dimensional reconstruction.It is different from traditional binocular camera calibration,it can be used in the large field of view to provide comprehensive three-dimensional information through the multiple perspectives.This paper adopts Zhang Zhengyou calibration algorithm,in the four directions using four cameras shot on calibration target which is a black and white X-corners in the scene to calculate the internal and external parameters of each camera firstly,Then through the relationship of ma?trix in cameras and the LM optimization algorithm to unify camera coordinate system,complete the multi-camera calibration system,This method can be applied to large scenario,for the complete information of three-dimensional reconstruction.Finally through the experiment, the experimental data is given to demonstrate the correctness of this method and proposed a relationship between the position of the camera and calibration precision.This method is applied to human motion capture system of power training and provides a new way of thinking for power training.

楚圣輝（1989-），男，河北石家莊人，碩士，研究方向為機器視覺、圖像處理

張慧萌（1988-），男，北京人，碩士，研究方向為電力系統仿真培訓、數字圖像處理

陳碩（1993-），女，北京人，碩士，研究方向為視覺測量，數字圖像處理

孟浩（1978-），女，漢族，內蒙赤峰人，博士，講師，研究方向為精密測量理論與技術、非統計理論

劉國忠（1966-），男，山西平遙人，博士，教授，研究方向為生物醫學檢測技術與儀器、光電測量技術及儀器

2017-03-14

2017-05-20

1007-1423（2017）15-0033-06

10.3969/j.issn.1007-1423.2017.15.008

Wide Field;Multi-view Calibration;Zhang Zhengyou Calibration Algorithm;X-corners