基于局部線性重構的近鄰填充算法

溫海標

（廣西師范學院計算機與信息工程學院，南寧 530023）

基于局部線性重構的近鄰填充算法

溫海標

（廣西師范學院計算機與信息工程學院，南寧 530023）

K近鄰填充算法（KNNI）對缺失數據填充時，使用K個近鄰的訓練樣本屬性值的平均值作為KNNI算法的填充值，該值偏離真實值較大，一種有效的方法是K近鄰樣本屬性值的加權平均值作為填充值。如何確定K近鄰樣本的權值，是KNNI算法研究熱點。為此，提出引入局部線性重構方法用于近鄰填充，該方法是用K近鄰樣本重構測試樣本得出權值。實驗結果表明提出的算法比KNNI算法填充效果更好，填充值更接近真實值。

缺失值填充；重構技術；K近鄰；LLR

0 引言

在機器學習的實際應用中，樣本的一些數據經常因為某些原因導致樣本數據不完整，例如數據暫時無法得到、被遺漏等原因導致數據缺失[1]。樣本數據的缺失會影響機器從樣本數據學習得來的模型性能或規則的正確性。因此在機器學習領域，缺失數據填充是基礎而又重要的研究問題。

目前，已有多種方法處理缺失值，例如最近鄰、決策樹、貝葉斯網絡、支持向量機、粗糙集和模糊集、神經網絡等方法[2]。其中K近鄰填充算法[3]時間復雜度低，填充效率和準確率高等優點受到了廣泛研究。其基本原理是通過相似度量函數計算出缺失樣本的K個近鄰完整樣本，計算求得K個樣本的均值作為填充值。KNNI（K-Nearest Neighbor Imputation）存在一個明顯的缺陷，如圖1，當K=3時，A、B、C樣本作為缺失樣本的近鄰，A、B、C樣本的均值作為缺失樣本的填充值，該值偏離真實值的偏差是較大的，因為C樣本離缺失樣本較遠，其中對填充值有較大影響。一個有效的方法是對A、B、C樣本設置權值，離缺失樣本越近，權值越大，即A最大，C最小，A、B、C樣本加權平均值作為缺失樣本的填充值。這種方法就是降低離缺失樣本較遠的整樣本的值對填充值的影響。本文用局部線性重構的方法用于KNNI算法，找出合適的K近鄰樣本權值，進一步降低填充值的偏差。

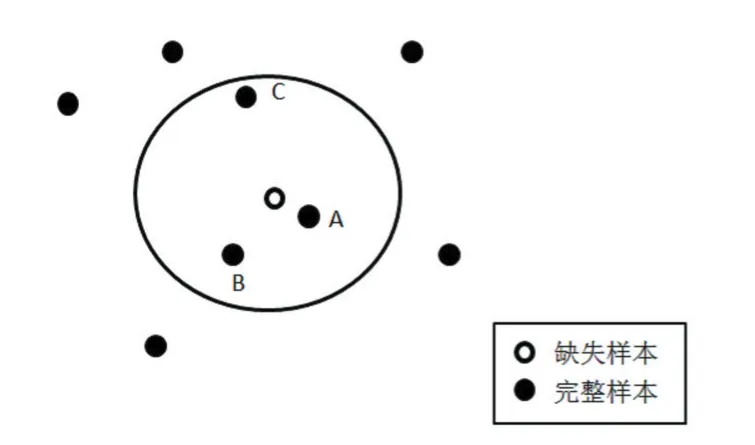
圖1 缺失樣本近鄰點選擇

1 LLR-KNNI算法

1.1 重構技術理論

一個向量被一組線性無關的向量線性組合近似表示，稱為重構[4]。已知一組線性無關向量x1，x2，x3，…，xk，xk∈Rd，和被這組線性近似表示的向量y，y∈Rd，其中d表示向量的元素個數，根據重構理論，得出如下函數：

式（1）中，wi為重構系數，值越大，說明xi向量的元素值和y向量元素值接近。W為重構系數向量。式（2）中的e為重構誤差，e的值越小，說明這組線性無關向量的近似表示的向量與y接近。目前重構技術的應用得到廣泛應用，如人臉識別、圖像去噪、屬性降維等[5]，其中屬性降維中的局部線性嵌入算法較為經典。局部線性嵌入（Locally Linear Embedding，LLE）算法[6]假設在一個高維樣本空間中某個流行局部小領域看成局部線性，即在這個小領域里的某點可以用重構技術被它周圍的點線性重構表示。高維樣本空間中，局部小領域的點是近鄰關系，降維后這些點仍然是近鄰關系，是一種基于流行的降維算法。LLE算法因計算復雜度低，需配置參數少，魯棒性好等優點得到了廣泛應用。

1.2 LLR-KNNI

局部線性重構（Local Linear Reconstruction，LLR）是基于重構理論和LLE算法得出并應用于KNNI算法中，局部指的是重構缺失樣本的完整樣本來自缺失樣本的某個領域，LLR-KNNI算法分為預處理和決策過程，預處理中，首先把數據樣本分為訓練樣本和測試樣本，具有完整數據的作為訓練樣本，含缺失數據的樣本作為測試樣本。樣本屬性可分為一般屬性和決策屬性，缺失樣本的缺失屬性值可以是一般屬性，也可以是決策屬性，LLR-KNNI算法把缺失屬性視為決策屬性，即當缺失屬性值是一般屬性的值時，該屬性作為決策屬性，其他為一般屬性。其次將整個數據樣本除決策屬性之外的其他屬性值規范化到[0，1]區間。決策過程中，每個缺失樣本通過相似度量函數計算出k領域的k個近鄰樣本，通過重構方法找出k個近鄰樣本的重構系數，這個系數稱為權值，權值越大，說明，該權值對應的近鄰樣本與缺失樣本越相似。最后加權求和得出填充值。算法描述如下：

訓練樣本X∈Rn×d，測試樣本Y∈Rm×d，m，n為樣本數，d為屬性個數。

步驟1數據樣本將非決策屬性規范化為[0，1]區間，規范化方法采用最小最大規范化法，如下式：

式（3）中，max和min分別表示樣本屬性A的最大值和最小值。

步驟2通過相似度量函數計算測試樣本的K個近鄰樣本，相似度量函數采用歐氏距離函數：

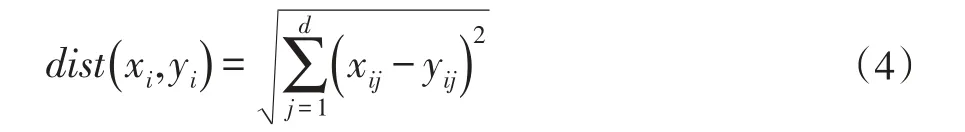
測試樣本與每個訓練樣本根據式（4）計算距離，計算結果從小到大排序，取前K個距離對應的樣本作為測試樣本的K近鄰樣本。

步驟3測試樣本的K近鄰樣本根據下式重構測試樣本

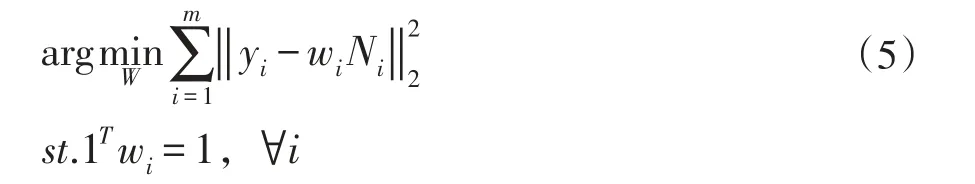
式（5）中，Ni∈Rk×d是近鄰樣本矩陣，存儲的是測試樣本的K個近鄰樣本，wi∈R1×k為近鄰樣本權值向量，W∈Rm×k為近鄰樣本權值矩陣。

步驟4通過求解式（5）的目標函數，得出測試樣本K個近鄰樣本的權值，假設樣本第j個屬性為決策屬性，根據下式計算試樣本的填充值：

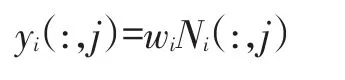
其中Ni（:，j）表示抽取矩陣Ni的第j個列向量。算法的偽代碼如下：

算法1 LLR-KNNI算法

輸入：訓練樣本X，測試樣本Y，近鄰個數K

輸出：測試樣本決策屬性值

2 實驗結果與分析

實驗的評價指標采用均方根誤差（Root Mean Square Error，RMSE），計算公式如下：

其中m為測試樣本的缺失值個數，yi*和yi分別為填充值和真實值。RMSE表明填充值和真實值之間的關系，RMSE值越小，說明填充值與真實值差值越小，即填充值越接近真實值。

實驗過程中，LLR-KNNI算法和KNNI算法分別對缺失樣本填充，分別計算RMSE值，作為比較LLRKNNI算法和KNNI算法的填充性能。

實驗部分的數據集選取UCI[7]機器學習知識庫中的部分數據集（表1）進行實驗，所選的數據集全部是無缺失值的完整數據集，以測試LLR-KNNI算法的填充性能。

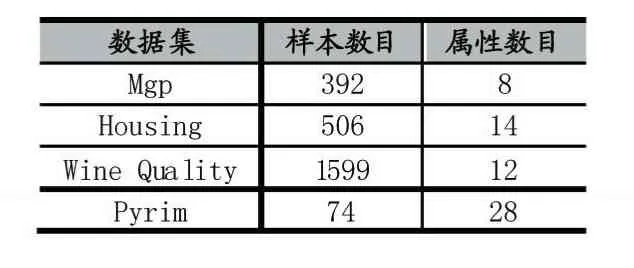
表1 實驗采用的UCI數據集

本文算法采用MATLAB軟件編程實現，MATLAB軟件版本為2014a。系統平臺為AMD AthlonⅡX2 B24 3.0 GHz，4GB內存，操作系統：Windows 7旗艦版。LLR-KNNI算法和KNNI算法近鄰個數K設置為5，實驗的驗證方法采用10折交叉驗證法，對數據集拆分10份，第一次實驗時，第1份設為測試集，其余為訓練集，第二次實驗將第2份設為測試集，其余為訓練集，此操作重復十次。對表1中的每個數據集采用10折交叉驗證法實驗十次，并取十次實驗得出的RMSE的均值加上標準差得出如表2。

從表2可以看出，在每個數據集上，LLR-KNNI算法的RMSE的值比KNNI的小，說明LLR-KNNI算法的填充值更接近真實值，即LLR-KNNI算法的填充性能優于傳統KNNI算法。從每個數據集中的標準差的值可以看出，LLR-KNNI算法的標準差值比KNNI的小，說明LLR-KNNI算法比KNNI算法有更好的穩定性。從圖2更直觀看出LLR-KNNI的優越性，也說明LLRKNNI算法比KNNI具有更好的填充性能。

表2 LLR-KNNI算法和KNNI算法在各數據集上RMSE的比較（均值標準差）

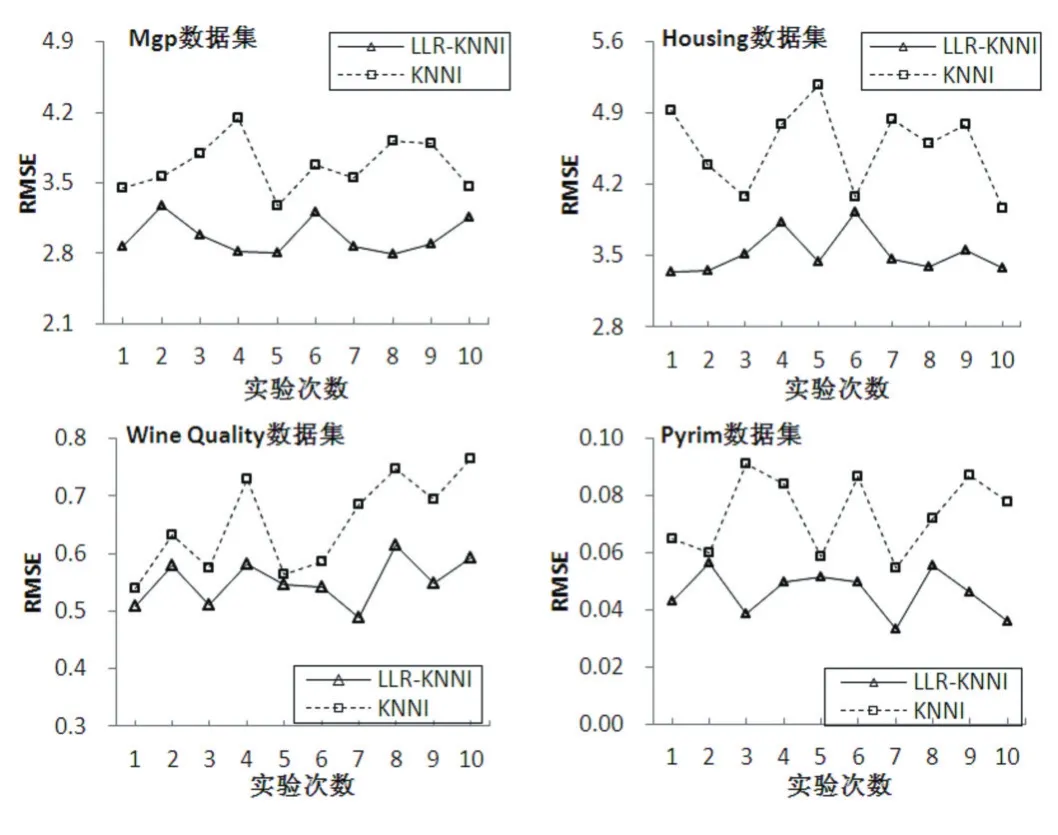
圖2 算法在各數據集十次實驗RMSE對比圖

3 結語

本文的LLR-KNNI算法，使用線性重構的方法得出樣本近鄰點的權值，近鄰樣本權值的大小說明與缺失樣本的相似程度，離缺失樣本越遠，近鄰樣本權值越小，一定程度降低KNNI算法中較遠的近鄰點對算法的填充性能影響。通過對比LLR-KNNI算法和KNNI算法的均方根誤差的實驗分析表明，LLR-KNNI算法的填充性能優于KNNI算法。

[1]Little，Roderick J A，Rubin，et al.Statistical Analysis with Missing Data[J].American Journal of Sociology，1988，26（Volume 94，Num-ber 1）:1322-39.

[2]Zhang S，Jin Z，Zhu X.Missing Data Imputation by Utilizing Information Within Incomplete Instances[J].Journal of Systems&Software，2011，84（3）:452-459.

[3]Cover T，Hart P.Nearest Neighbor Pattern Classification[J].IEEE Transactions on Information Theory，1967，13（1）:21-27.

[4]Kang P，Cho S.Locally Linear Reconstruction for Instance-Based Learning[J].Pattern Recognition,2008,41（11）:3507-3518.

[5]Zhang L,Chen C,Bu J,et al.Active Learning Based on Locally Linear Reconstruction[J].IEEE Transactions on Pattern Analysis& Machine Intelligence,2011,33（10）:2026-38.

[6]Roweis S T,Saul L K.Nonlinear Dimensionality Reduction by Locally Linear Embedding[J].Science,2000,290（5500）:2323-6.

[7]UCI Repository of Machine Learning Datasets[DB/OL].http://archive.ics.uci.edu/-m.

Nearest Neighbor Filling Algorithm Based on Local Linear Reconstruction

WEN Hai-biao

（School of Computer and Information Engineering,Guangxi Teachers Education University，Nanning 530023）

Knearest neighbor filling algorithm for filling missing data,the average value of training sample attributes uses Kneighbor values as the filling value of KNNI algorithm,the value is far from the real values,an effective method is to sample attribute weighted Knearest neighbor average as filling value.How to determine the weights of Knearest neighbor samples is a hot research topic of KNNI algorithm.For this reason,proposes a method of local linear reconstruction for nearest neighbor filling.The method uses the Knearest neighbor sample to reconstruct the test sample.The experimental results show that the proposed algorithm is better than the KNNI algorithm,and the filling value is close to the real value.

溫海標（1989-），男，廣東河源人，碩士研究生，研究方向為數據挖掘、機器學習

2017-03-24

2017-05-15

1007-1423（2017）15-0003-04

10.3969/j.issn.1007-1423.2017.15.001

Missing Values Filling;Reconstruction Technique;KNearest Neighbor;LLR