探究高中數(shù)學(xué)教學(xué)中如何培養(yǎng)學(xué)生的求異思維

吳長山

(江蘇省新沂市高級(jí)中學(xué)，江蘇 新沂 221400)

?

探究高中數(shù)學(xué)教學(xué)中如何培養(yǎng)學(xué)生的求異思維

吳長山

(江蘇省新沂市高級(jí)中學(xué)，江蘇 新沂 221400)

本文結(jié)合作者工作實(shí)際，探討了高中數(shù)學(xué)教學(xué)過程中，如何培養(yǎng)學(xué)生的求異思維，希望通過研究分析能提升學(xué)生們的學(xué)習(xí)能力，僅供參考.

高中；數(shù)學(xué)；教學(xué)；培養(yǎng)；求異思維；能力；分析

高中數(shù)學(xué)是一門相對(duì)復(fù)雜的學(xué)科，具備的知識(shí)內(nèi)容也非常復(fù)雜，而在教學(xué)過程中，很多老師采用的是“灌輸式”的教學(xué)方式開展教學(xué)，學(xué)生也只能跟著老師的方式聽課，不能夠互動(dòng)只能自己思考琢磨，這不利于學(xué)生掌握知識(shí).重視學(xué)生的求異思維與創(chuàng)新精神是新課改后提出來的基本要求，培養(yǎng)學(xué)生這兩方面內(nèi)容能夠幫助學(xué)生提高解題能力.因此，探討如何培養(yǎng)學(xué)生的求異思維是本課題研究的重點(diǎn).

一、為學(xué)生提供進(jìn)行求異思考的機(jī)會(huì)

在教學(xué)過程中，讓學(xué)生求異思維得到發(fā)展是教學(xué)的核心任務(wù)，在高中數(shù)學(xué)教學(xué)過程中，需要老師積極創(chuàng)設(shè)各種問題情境，讓學(xué)生在情境模式中進(jìn)行題型思考，從而培養(yǎng)異思維.例如，在教學(xué)過程中，老師可以把指數(shù)函數(shù)在底數(shù)不同的條件下的函數(shù)，以多媒體圖象的方式展示給學(xué)生，然后再通過電腦將圖象的性質(zhì)打亂，之后在讓學(xué)生進(jìn)行圖象重組，這樣的方式不僅能夠讓學(xué)生全面增加對(duì)指數(shù)函數(shù)的認(rèn)識(shí)，而且還能在一定的程度上讓學(xué)生理解問題內(nèi)容，能夠通過研究分析得出正確答案.

二、運(yùn)用啟發(fā)與誘導(dǎo)方式讓學(xué)生有意識(shí)進(jìn)行質(zhì)疑和求異

對(duì)于高中生而言，雖然 他們具備一定的學(xué)習(xí)能力自律能力，但是針對(duì)一些能力的形成，還是需要老師在教學(xué)過程中，不斷地對(duì)其進(jìn)行誘導(dǎo)和鼓勵(lì).

例如：在蘇教版“函數(shù)”知識(shí)點(diǎn)學(xué)習(xí)的過程中，對(duì)于學(xué)生的求異思維培養(yǎng)，老師可以通過使用函數(shù)的三要素、基本性質(zhì)、表示方法等知識(shí)對(duì)學(xué)生進(jìn)行啟發(fā).例如：“函數(shù)f(x)具備奇偶性的條件是那些？會(huì)不會(huì)是函數(shù)f(x)=0？”

針對(duì)該問題，很多學(xué)生都認(rèn)為老師的答案是正確的，自己本身沒有進(jìn)行認(rèn)真的思考，就錯(cuò)誤地認(rèn)為答案是f(x)=0.

而老師針對(duì)該現(xiàn)象需要積極地做好學(xué)生的啟發(fā)與引導(dǎo)工作.讓學(xué)生了解函數(shù)的奇偶性的條件是什么.通過老師的引導(dǎo)和啟發(fā)，學(xué)生會(huì)明白：奇函數(shù)為f(-x)=-f(x)；偶函數(shù)為：f(-x)=f(x).

在學(xué)生掌握這些知識(shí)后，接下老師就可以繼續(xù)提問，奇函數(shù)和偶函數(shù)的圖象關(guān)系具備哪些相似點(diǎn)？此時(shí)學(xué)生就可以自如回答：奇函數(shù)的圖象關(guān)于原點(diǎn)對(duì)稱，偶函數(shù)的圖象關(guān)于y軸對(duì)稱.老師就可以繼續(xù)提問學(xué)生：這兩個(gè)特點(diǎn)有什么交集的地方？此時(shí)，老師提出問題后，可以適當(dāng)?shù)貙?duì)學(xué)生進(jìn)行誘導(dǎo)，并且鼓勵(lì)學(xué)生勇于思考問題，在激發(fā)學(xué)生以及鼓勵(lì)學(xué)生后，最后就將答案得出：f(x)定義域關(guān)于原點(diǎn)對(duì)稱.

三、細(xì)心設(shè)置練習(xí)題型，讓學(xué)生在解題中形成求異思維

在高中數(shù)學(xué)學(xué)習(xí)過程中，需要掌握的數(shù)學(xué)知識(shí)結(jié)構(gòu)非常繁雜，這也是有數(shù)學(xué)自身的性質(zhì)決定的.大量的理論、公式進(jìn)行結(jié)論論證是高中數(shù)學(xué)的特點(diǎn)，因此，老師在高中習(xí)題設(shè)計(jì)的過程中，需要從學(xué)生的角度進(jìn)行思考，要以多方面的角度對(duì)數(shù)學(xué)習(xí)題進(jìn)行設(shè)計(jì)，從而讓學(xué)生能在輕松無壓力的條件下將求異思維培養(yǎng).

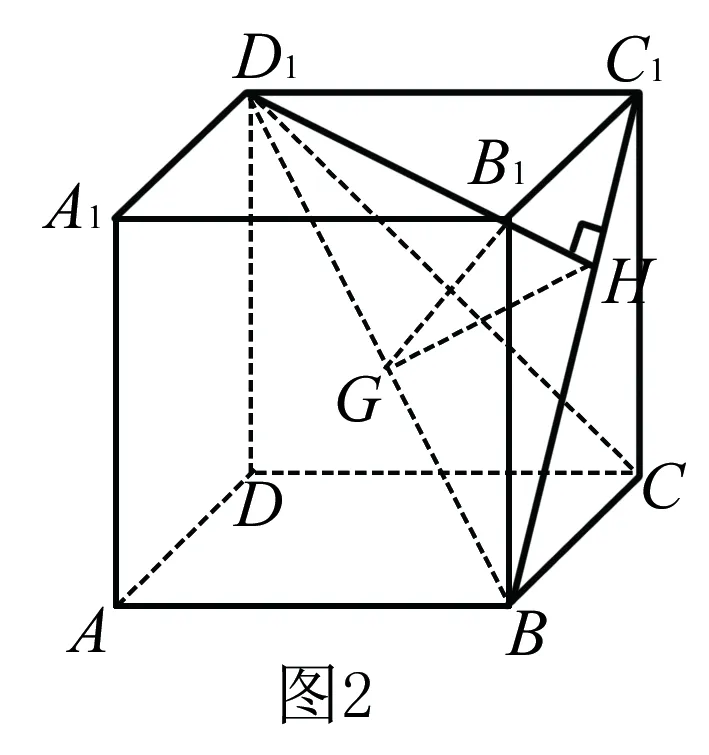
例如，在對(duì)正四棱柱知識(shí)點(diǎn)學(xué)習(xí)的過程中，在對(duì)“BD1與面B1BCC1形成的角為30°，求異面直線BD1和AD所成的角”解答時(shí)，老師可以把傳統(tǒng)平面求角度的問題，轉(zhuǎn)變成異面求角度的問題.所以，在進(jìn)行此類題目解答時(shí)，老師可以引導(dǎo)性地帶領(lǐng)學(xué)生去思考：直線AD和那條直線是平行的？這兩者關(guān)系與BD1又是什么關(guān)系？這些信息能夠給解答問題提供哪些幫助？最后學(xué)生在通過運(yùn)算后，將答案得出：異面直線BD1與AD成為的角度為60°.

總之，在高中數(shù)學(xué)教學(xué)過程中，老師要重視對(duì)學(xué)生的求異思維培養(yǎng)，要讓學(xué)生在數(shù)學(xué)知識(shí)學(xué)習(xí)以及題型解題的過程中，能夠有效地將發(fā)散思維與集中思維結(jié)合在一起.

[1]焦玉增.演示實(shí)驗(yàn)中如何培養(yǎng)學(xué)生的思維能力[J]. 學(xué)周刊，2017(05).

[2]王臘梅.淺談在初中物理實(shí)驗(yàn)教學(xué)中如何培養(yǎng)學(xué)生的創(chuàng)新思維能力[J]. 學(xué)周刊， 2017(09).

[責(zé)任編輯：楊惠民]

2017-05-01

吳長山(1978-)，江蘇新沂人，學(xué)士，中學(xué)一級(jí)教師，主要從事高中數(shù)學(xué)教學(xué)研究.

G632

B

1008-0333(2017)18-0033-01