基于LS-SVR的壓力傳感器溫度自補償策略*

胡啟陽,龍 軍,陳 君

(北京控制工程研究所,北京 100190)

?

基于LS-SVR的壓力傳感器溫度自補償策略*

胡啟陽,龍 軍,陳 君*

(北京控制工程研究所,北京 100190)

硅壓阻式壓力傳感器在實際使用過程中受環境溫度影響易發生溫度漂移,同時傳感器本身又存在一定的非線性,這使得傳感器測量精度大幅度降低。針對傳統的溫度補償方法中需引入溫度傳感器的情況,提出一種基于最小二乘支持向量回歸(LS-SVR)的壓力傳感器溫度自補償策略,通過定義并測量傳感器橋路自身參數獲取溫度信息實現溫度補償,而無需配置額外的溫度傳感器。通過粒子群算法和交叉驗證對LS-SVR的參數進行了優化。實驗結果表明:這種利用傳感器自身橋路進行溫度補償的方法能夠有效地消除壓力傳感器的溫度漂移。補償后測量精度達到0.1%FS。

壓力傳感器;溫度補償;最小二乘支持向量回歸;粒子群優化;K-折交叉驗證

硅壓阻式壓力傳感器利用組成惠斯通電橋的4個半導體等值電阻在受到壓力時阻值會發生變化,從而打破電橋平衡,產生電壓輸出。由于半導體材料本身對環境溫度非常敏感,在壓力不變的情況下,傳感器的輸出會隨著溫度的變化產生漂移,使傳感器精度大大降低。因此,必須采取有效措施,補償傳感器由于溫度影響造成的誤差,從而提高傳感器的測量精度。

通常采用的補償方法有硬件補償法和軟件補償法。硬件補償法指采用硬件電路進行補償,存在調試困難,精度低,通用性差等缺點,不利于工程應用。軟件補償方法則是通過數學算法來構建測量模型,具有補償精度高,通用性強的特點。常用的軟件補償方法包括查表法,插值法,神經網絡等。查表法和插值法對數據點數隨著精度的要求急劇增加,而神經網絡算法存在訓練速度慢,容易陷入局部最小點,泛化能力差的局限性[1-2]。

支持向量機[3]SVM(Support Vector Machines)是一種基于結構風險最小化準則的機器學習方法。其中,被用于函數回歸的SVM常被稱為支持向量回歸SVR(Support Vector Regression)。和其他回歸算法相比,SVR能夠較好地解決小樣本,非線性,過擬合等實際應用問題。最小二乘支持向量回歸[4](LS-SVR)在支持向量回歸的基礎上,將不等式約束轉化為等式約束,用解線性方程組的方法代替求解二次規劃問題,在保持SVR優點的同時大大提高了計算速度[5-6]。

本文采用基于粒子群算法參數優化的LS-SVR進行溫度補償,同時從壓力傳感器元件本身獲取溫度信息。該方法無需布置額外的溫度傳感器進行測溫,在結構上更為簡單,同時克服了傳感器之間存在的溫度差問題,能有效提高傳感器的測量精度。

1 最小二乘支持向量回歸模型

對于給定訓練數據集(xi,yi)(i=1,2,…,l),LS-SVR的基本原理是通過非線性映射將輸入數據映射到高維空間,并在此空間中構造如下的估計模型

y(x)=?Tφ(x)+b

(1)

式中:φ(·)為非線性變換,?為對應的權向量,b為偏移量。

依據結構風險最小化原則,需求解如下優化問題

(2)

式中:γ是正則化因子,ei是訓練誤差。

為求解上述優化問題,引入拉格朗日乘子λi,構造如下拉格朗日函數:

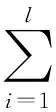
(3)

根據庫恩—塔克爾KKT(Karush-Kuhn-Tucker)條件,令L對各項偏導數為0,得

(4)

消去變量?,e則轉化為如下方程

(5)

式中:I是單位陣;Θ=[1,…,1]T,Ω中的元素Ωij=φ(xi)T(xj)

通過求解式(5)可得LS-SVR的回歸函數

(6)

式中:核函數K(xi,x)=φ(xi)Tφ(x)為滿足mercer條件的核函數。常用的核函數有多項式核函數,線性核函數和徑向基核函數等。本文選擇靈活性強,使用范圍廣,回歸精度較高的徑向基核函數,其表達式為

K(x,xi)=exp(-‖x-xi‖2/2σ2)

(7)

式中:σ為徑向基寬度。

2 粒子群算法和交叉驗證優化參數

由LS-SVR模型可知,正則化參數γ決定了訓練誤差的大小和泛化能力的強弱;徑向基寬度σ反映了訓練樣本數據在高維特征空間分布的復雜程度。這兩個參數的選取直接影響模型的性能,因此有必要通過優化來選取最佳的參數組合。常用的參數優化方法包括網格搜索法、梯度法、遺傳算法以及粒子群優化等[7-9]。

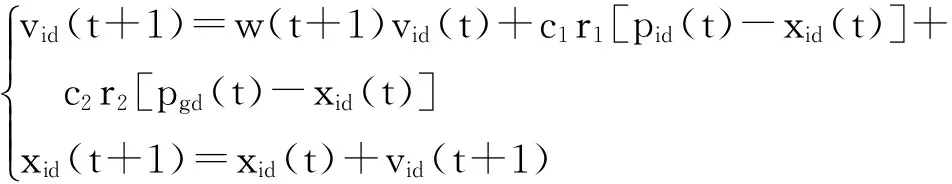
(8)

式中:w為慣性權重;r1,r2是[0,1]上的隨機數;c1,c2是學習因子;t為迭代次數。為使模型在前期具有較強的全局搜索能力,而后期具有較強的局部搜索能力,w按式(9)的線性遞減方式進行計算。

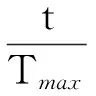
(9)

式中:wmax,wmin為預設的慣性權重最大值和最小值;Tmax為最大迭代次數。

交叉驗證CV(Cross Validate)是一種消除取樣隨機性所帶來的訓練偏差的統計方法[11]。k折交叉驗證是其中的常用方法。它將訓練數據隨機分為k個子集,以任一子集作為驗證集,其余k-1個子集作為訓練集進行建模,得到模型的均方誤差。這樣循環k次,直到k個子集都作為驗證集被預測一次。最后將k次預測所得均方根誤差的平均值作為最終的適應度值。本文在粒子群參數優化算法中采用五折交叉驗證法對參數組合進行評價,其適應度函數如式(10)所示:

(10)

應用粒子群算法和交叉驗證進行LS-SVR參數優化具體步驟如下:①初始化參數,即設定參數γ和σ的選擇范圍,慣性權重、學習因子、種群規模和迭代次數的值。②對每一粒子所對應的參數組合(γ,σ),應用LS-SVR進行建模,并按照式(10)進行適應度的計算。③按式(17)、式(18)對粒子的速度和位置進行更新,生成新一代種群。每迭代一次,需要對粒子的個體最優值和全局最優值進行重新定位,直到達到迭代次數。最后得到的使適應度最小的參數組合即為最優值[12]。

3 基于LS-SVR的壓力傳感器溫度自補償模型與仿真結果分析

3.1 補償原理

由于傳感器的測量值由壓力和溫度共同決定,因此在溫度補償的過程中,必須提取反應溫度變化的參量。常用的方法是通過外加一個溫度傳感器進行溫度的測量。由于溫度傳感器的測量值與壓力膜片實際溫度之間存在誤差,會給溫度補償精度帶來很大的影響。本文提出一種直接從壓力傳感器橋路元件本身來提取溫度變化參量的方法,從而實現溫度的自補償,從而進一步提高壓力傳感器的測量精度。

硅壓阻式壓力傳感器測量電路如圖1所示[13]。

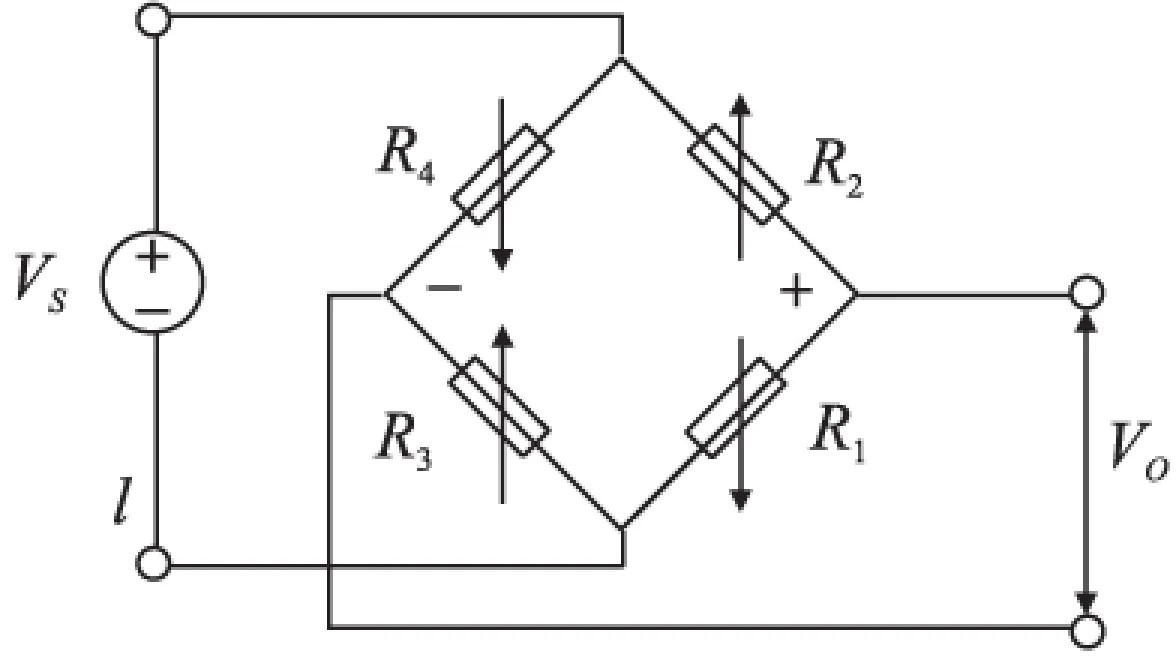
圖1 壓力傳感器測量橋路原理

其輸出電壓可表示為

(11)

在實際測量過程中,4個橋臂電阻的阻值不僅隨著壓力的變化而變化,還會隨著溫度的變化而變化。假設4個橋臂電阻初始阻值,溫度系數和壓阻系數一致,當溫度,壓力發生變化時,各電阻的阻值如下[14]:

(12)

式中:RO為0 ℃時候的電阻值,ΔRp為受壓力影響的變化量,ΔRt為受溫度影響的變化量。

測量橋路的并聯總電阻RA為(R1+R2)//(R3+R4),有

(13)

將式(12)代入式(13),得RA=RO+ΔRT,這是一個僅與溫度有關的值,不受壓力的影響。因此可以將RA作為主要反映溫度變化的參量。其值可由式(4)計算得到:

RA=Vs/I

(14)

式中:I為橋路電流。

同時定義

RB=Vo/I

(15)

將式(13)、式(14)代入式(15),易得

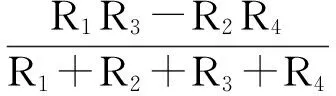
(16)

由于R1、R2、R3、R4均會受到壓力P和溫度T的影響,是溫度和壓力的二元函數,因此RA和RB也可以表示為P,T的二元函數形式

(17)

消去變量T,則可將待測壓力P表示為RA和RB的二次函數形式,即

P=f(RA,RB)

(18)

圖2 溫度補償原理圖

為了獲得橋路電流I,本文在電路中引入高精密低溫漂參考電阻RREF(精度0.05%,溫漂5 ppm),其測量原理圖如圖2所示,橋路電流I可表示為I=VREF/RREF。RA和RB可由式(19)進行計算:

(19)

3.2 模型建立

以電阻值RA,RB作為輸入,對應的壓力值作為輸出,建立基于LS-SVR的壓力傳感器溫度自補償模型。模型結構如圖3所示。

3.3 樣本獲取

選用某型0～2.0 MPa硅壓阻式壓力傳感器作為檢測元件,其工作范圍為-10 ℃～50 ℃。傳感器橋臂電阻為R=2.8 kΩ,精密參考電阻取值為2.2 kΩ。

為覆蓋被測元件的工作溫度范圍,實驗中在-15 ℃～55 ℃范圍內選取13個溫度點,每個溫度點上選擇15個壓力點,測量195組數據點對應的RA和RB值,如表1所示(表中數據為經保留小數點后兩位的結果)。

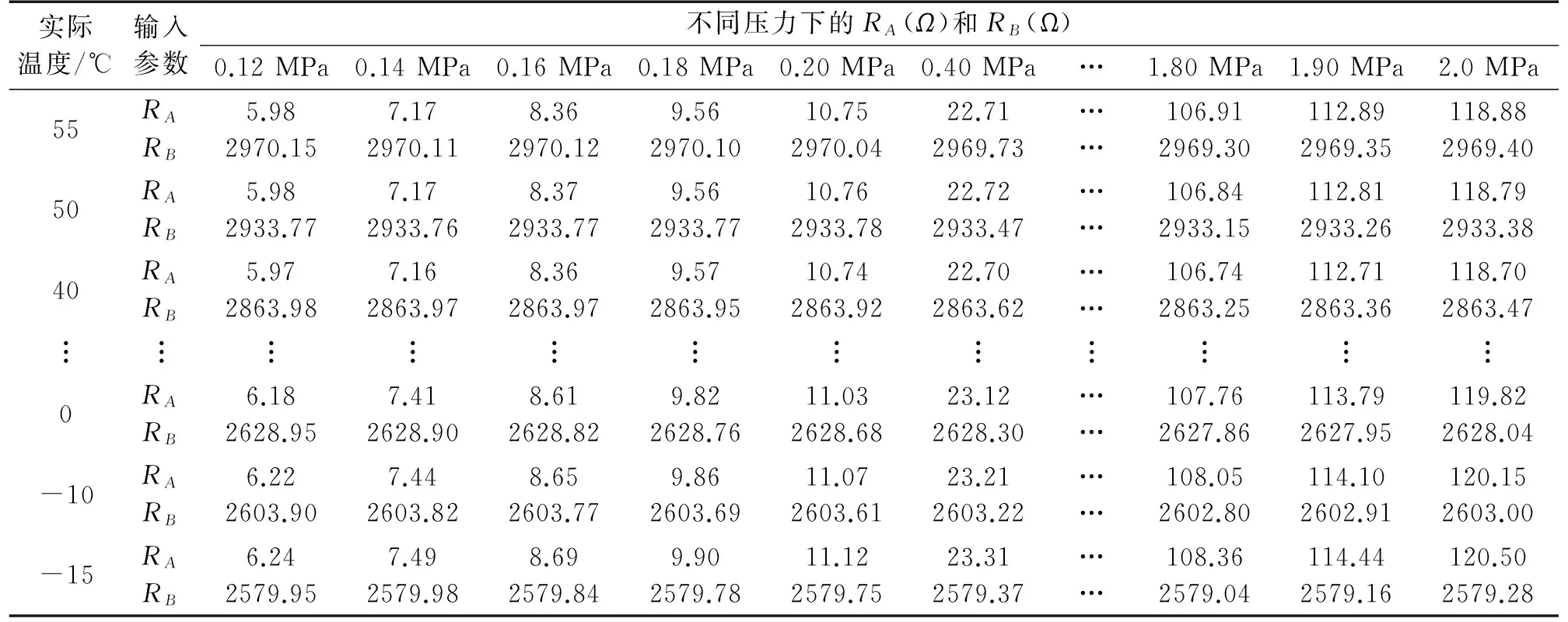
表1 傳感器標定數據

3.4 實驗過程和結果

將壓力標定值為0.12 MPa、0.16 MPa、0.2 MPa、0.6 MPa、1.0 MPa、1.4 MPa、1.8 MPa和2.0 MPa所對應的104組數據作為測試集,其余91組數據樣本作為驗證集。首先利用測試集的數據,按照本文第3節中的方法進行參數優化。參數設定為:wmax=0.95,wmin=0.4,種群規模m=50,最大迭代次數Tmax=300,學習因子c1=c2=2。優化過程如圖4所示。

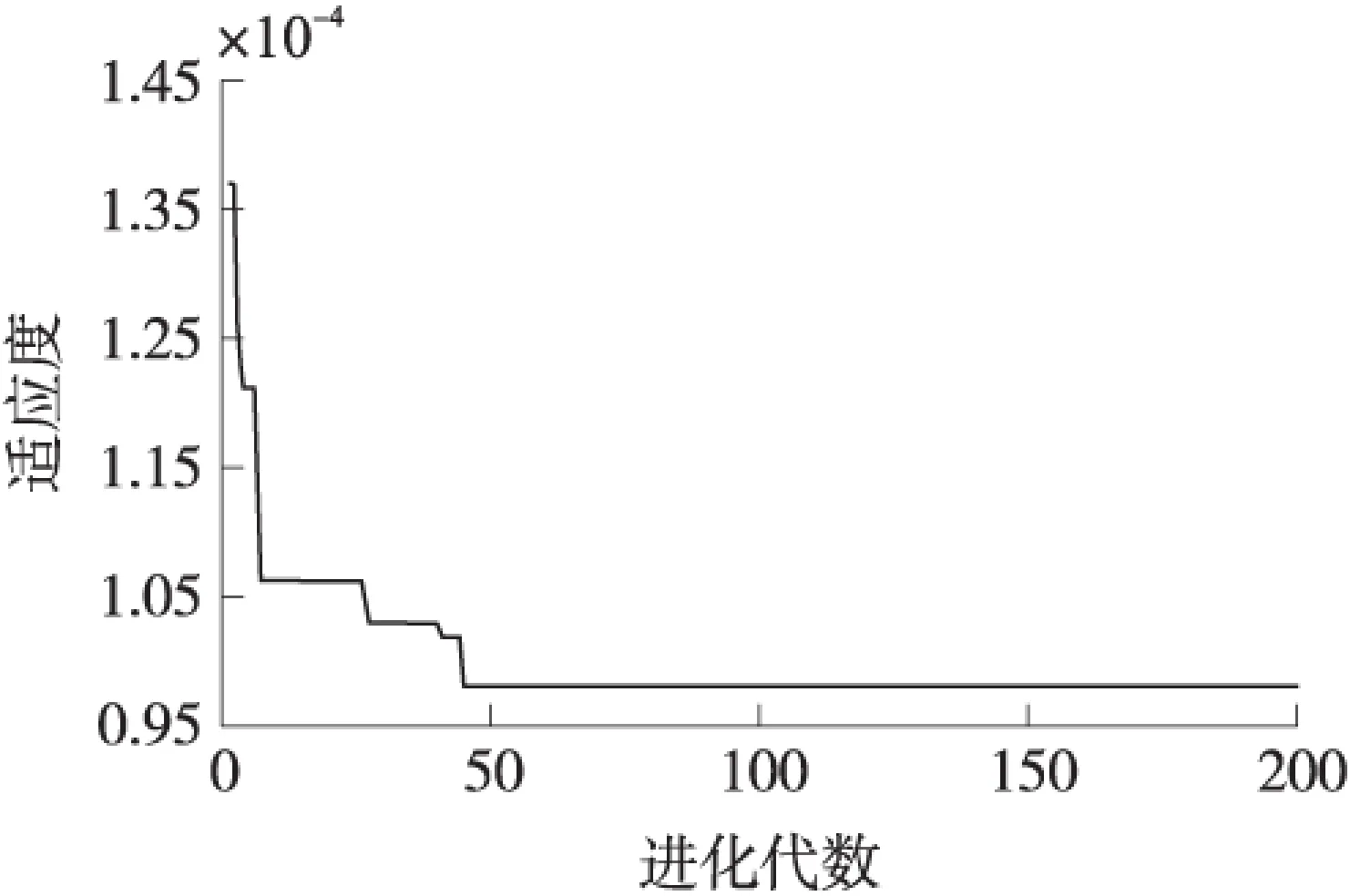
圖4 粒子群優化曲線

由圖4可以看出,優化過程在50步以內即可達到收斂。利用優化后的參數重新建立LS-SVR溫度補償模型,并利用驗證集的數據進行預測,預測結果作為溫度補償后的壓力值。限于篇幅,選擇壓力傳感器工作范圍內的6個溫度點-10 ℃、0 ℃、15 ℃、25 ℃、40 ℃和50 ℃分別作出進行溫度補償前后的壓力真實值與測量值(預測值)曲線如圖5所示。

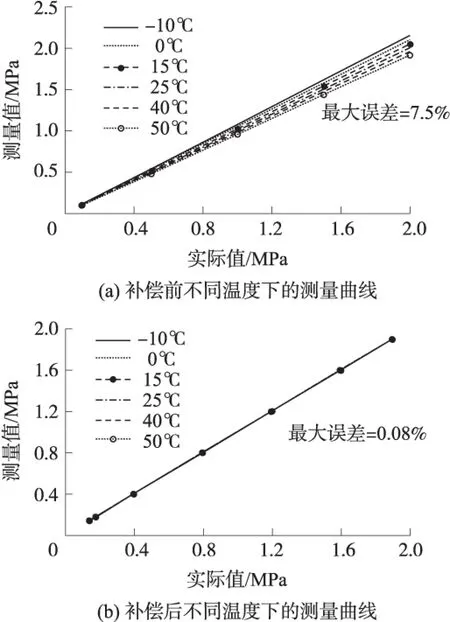
圖5 補償前后不同溫度下測量曲線對比圖

由圖5可知,在進行溫度補償之前,隨著溫度的升高,同一壓力下的測量值在降低,因此壓力傳感器中存在明顯的溫度漂移,且漂移量隨著待測壓力的增加而升高,滿量程誤差達到了7.5%通過LS-SVR模型進行溫度補償后的各溫度下測量曲線一致性較好,測量誤差在0.1%以內。

兩幅圖的對比結果表明,采用測量參數RA和RB并用LS-SVR的方法建立的溫度補償模型能夠有效地消除溫度對傳感器測量的影響,補償后的精度提高到了0.1%以內,取得了良好的補償效果。

4 結論

本文針對硅壓阻式壓力傳感器存在的溫度漂移問題,利用壓力傳感器敏感橋路本身對溫度和壓力敏感的特點,采用LS-SVR建立了其與被測壓力之間的測量模型,采用粒子群算法和交叉驗證方法對模型參數進行優化。最終獲得的壓力測量模型極大地消除了溫度對壓力測量的影響,將壓力測量精度提高到0.1%以內,同時由于避免設置額外的的溫度傳感器獲得溫度信息,因此該方法還具有很強的工程實用價值。

[1] 楊雪,劉詩斌. 壓力傳感器溫度補償各種算法的比較分析[J]. 電子設計工程,2013,21(10):90-96.

[2] 楊遂軍,康國煉,葉樹亮. 基于最小二乘支持向量機的硅壓阻式傳感器溫度補償[J]. 傳感技術學報,2016,29(4):500-505.

[3] Vapnic V. Statistical Learning Theory[M]. New York:John Wiley,1998.

[4] Suykens J A K,Vandewalle J. Least Squares Support Vector Machine Classifiers[J]. Neural Processing Letters,1999,9(3):293-300.

[5] Wang H F,Hu D J. Comparison of SVM and LS-SVM for Regression[C]//Processing of 2005 International Conference on Neural Networks and Brain. Beijing,China:IEEE,2005:279-283.

[6] 閻威武,邵惠鶴. 支持向量機和最小二乘支持向量機的比較及應用研究[J]. 控制與決策,2008,18(3):358-360.

[7] 陳偉根,騰黎,劉軍,等. 基于遺傳優化支持向量機的變壓器繞組熱點溫度預測模型[J]. 電工技術學報,2014,29(1):44-51.

[8] 劉昌平,范明鈺,王光衛,等. 基于梯度算法的支持向量機參數優化方法[J]. 控制與決策,2008,23(11):1291-1295.

[9] 韓曉慧,杜松懷,蘇娟,等. 基于參數優化的最小二乘支持向量機觸電電流檢測方法[J]. 農機工程學報,2014,30(23):238-245.

[10] 張朝龍,紅巨浪,李彥梅,等. 基于云粒子群—最小二乘支持向量機的傳感器溫度補償[J]. 傳感技術學報,2012,25(4):472-477.

[11] 紀昌明,周婷,向騰非,等. 基于網格搜索和交叉驗證的支持向量機在梯級水電系統隱隨機調度中的應用[J]. 電力自動化設備,2014,34(3):125-131.

[12] 段其昌,周華鑫,曾勇,等. 帶擴展記憶的粒子群優化最小二乘支持向量機在中長期電力負荷預測中的應用[J]. 計算機科學,2013,40(6):41-43.

[13] 龍軍,關威,汪旭東,等. 基于嶺回歸的壓力傳感器高精度測量模型研究[J]. 傳感技術學報,2017,30(3):391-396.

[14] 姚敏,趙敏,邢力. 基于小波神經網絡的壓力傳感器溫度補償方法[J]. 傳感器技術,2005,24(7):13-15.

胡啟陽(1991-),男,碩士,2016年畢業于北京控制工程研究所,主要研究方向為傳感器技術,674700313@qq.com;

龍 軍(1985-),男,博士,2013年畢業于浙江大學,主要研究方向為傳感器技術,18613889712@163.com;

陳 君(1978-),男,碩士,2004年畢業于西北工業大學,主要研究方向為傳感器技術,航天器推進技術,sportcj@163.com。

Temperature Self-Compensation Strategy forPressure Sensor Based on LS-SVR*

HU Qiyang,LONG Jun,CHEN Jun*

(Beijing Institute of Control Engineering,Beijing 100190,China)

Temperature drift exists in Silicon piezo-resistive pressure sensor as the result of its susceptibility to temperature,which decreases the measurement precision of the sensor. Aiming at the problem that a temperature sensor is needed in traditional temperature compensation method,a temperature self-compensation strategy for pressure sensor based on LS-SVR is proposed,which acquires temperature information by definition and measurement of parameters in the measurement bridge of sensor. PSO algorithm and Cross Validate are applied to optimize the parameters of LS-SVR. The experimental results show that this method can eliminate the temperature drift effectively without an additional temperature sensor. The measurement accuracy can be improved to 0.1%FS.

pressure sensor;temperature compensation;LS-SVR;PSO;K-fold CV

項目來源:十二五民用航天項目(E020415)

2016-09-07 修改日期:2017-03-17

TP212

A

1004-1699(2017)07-1057-05

C:7230

10.3969/j.issn.1004-1699.2017.07.015