鎧裝熱電偶傳遞函數參數估計*

李文軍,孫宏健,鄭永軍

(中國計量大學計量測試工程學院,杭州 310018)

?

鎧裝熱電偶傳遞函數參數估計*

李文軍*,孫宏健,鄭永軍

(中國計量大學計量測試工程學院,杭州 310018)

為了評價鎧裝熱電偶動態特性,針對鎧裝熱電偶測量動態溫度過程用集總熱容法和復合集總熱容法建立了鎧裝熱電偶的傳熱模型。從所建立模型分析,鎧裝式熱電偶傳熱過程是保護管、絕緣層和測量接點這3個小時間常數慣性環節的串聯,且保護管與絕緣層、絕緣層與測量接點存在接觸熱阻,產生了兩個耦合作用。當保護管時間常數和絕緣層時間常數都比較小時,傳遞函數可近似為帶時滯的慣性環節。建立了基于雙槽法的正負溫度階躍實驗系統,測量熱電偶在正負溫度階躍激勵下的輸出響應。按照預估延遲時間和預估延遲時間加擾動兩種情形,用輸出誤差自回歸滑動平均方法估計了傳遞函數的參數。結果表明,輸出誤差自回歸滑動平均方法適用于鎧裝熱電偶實驗建模和模型的離線辨識。

鎧裝熱電偶;集總熱容法;傳遞函數;自回歸滑動平均

工業測量中存在著測量動態溫度的需求[1-2],以及對溫度傳感器動態特性做測試的需求[3-5]。作為溫度傳感器,熱電偶和鎧裝熱電偶得到了廣泛應用。為了用熱電偶測量動態溫度,工業測量中常通過組合方式比如利用雙偶或三偶組合實現動態測溫[6-8]。同時為了提高鎧裝熱電偶測量動態溫度的精度,還利用系統辨識技術進行實驗建模以近似得到系統模型進行補償[9-11]。

由于鎧裝熱電偶測量端存在接觸熱阻以及多重換熱[12],其測溫過程物理上構成一個延遲系統,采用理論建模和實驗建模結合的方式,能更準確地描述鎧裝熱電偶的動態特性以獲得較好的測量結果[13-14]。

本文首先利用集總熱容法以及復合集總熱容法進行理論建模[15-16],建立了3種鎧裝熱電偶測量端的傳熱模型,并給出了傳遞函數結構。其次介紹利用雙槽法所建立的實驗系統,該實驗系統用來取得鎧裝熱電偶在正負溫度階躍激勵下的輸入和輸出。然后,根據鎧裝熱電偶輸入和輸出進行實驗建模,用輸出誤差類模型來度量模型和過程之間的誤差,具體采用輸出誤差類模型中的自回歸滑動平均模型建立鎧裝熱電偶的系統辨識模型。最后,以一種快響應鎧裝熱電偶為對象,以理論推導的傳遞函數為先驗結構,采用自回歸滑動平均模型,用最小二乘迭代法對其實驗工況下的參數進行了估計,給出了兩個算例。

1 鎧裝熱電偶傳熱模型

1.1 露端式鎧裝熱電偶的集總熱容模型

鎧裝熱電偶主要分露端式、絕緣式和接殼式3種。其中露端式鎧裝熱電偶的結構圖如圖1所示,其結構特征是熱電偶接點從保護管中伸出。

圖1 露端式鎧裝熱電偶幾何結構

露端式鎧裝熱電偶的測量接點對被測介質溫度變化的響應,受到介質與測量接點之間外部熱阻以及接點內部熱阻影響。由于內部熱阻遠遠小于外部熱阻,可以采用集總熱容法描述其換熱過程,如圖2所示。

圖2 露端式鎧裝熱電偶的集總熱容模型

測量接點與測介質之間的換熱方程為[17]:

(1)

初始條件為:

T1(0)=T0式中:h為熱電偶測量接點與被測介質之間的換熱系數(當被測介質為固體,則h為測量接點與被測固體表面之間的接觸系數,接觸系數與換熱系數具有相同的量綱),單位為W/(m2·K);A為熱電偶測量接點與被測物體之間換熱的面積,單位為m2;T1(t) 為測量接點溫度,T2(t)為被測介質溫度,單位為K;c為測量接點比熱,單位為J/(kg·K);ρ為測量接點密度,單位為kg/m3;V為測量接點體積,單位為m3;t為時間,單位為s。

為簡便起見采用過余溫度,記:

Tb(t)=T1(t)-T0

Tg(t)=T2(t)-T0

則式(1)以及初始條件變為:

(2)

對式(2)做拉普拉斯變換,得到露端式鎧裝熱電偶傳遞函數為:

(3)

即一階慣性系統模型。

1.2 絕緣式鎧裝熱電偶的復合集總熱容模型

絕緣式鎧裝熱電偶的結構如圖3所示,其結構特征是測量接點在保護管內,且測量接點和保護管端面之間有絕緣填充物如氧化鎂[18]。

圖3 絕緣式鎧裝熱電偶幾何結構

圖4 絕緣式鎧裝熱電偶的復合集總熱容模型

從圖3可以看到,保護管、絕緣層和測量接點構成一個復合式熱傳導系統。測量接點對被測介質溫度變化的響應受到若干個熱阻影響:被測介質與保護管端面外壁之間熱阻、保護管層內熱阻、保護管端面內壁與絕緣層之間熱阻、絕緣層內部熱阻、絕緣層與接點之間熱阻、接點內部熱阻,如圖4所示。當保護管為金屬、絕緣層為氧化鎂時,保護管層和絕緣層內部熱阻以及接點的內部熱阻遠小于其他幾個熱阻,因此,被測介質、保護管端面、絕緣層和測量接點之間的傳熱可以視為復合集總熱容模型[19]。利用復合集總熱容法,可分別寫出保護管、絕緣層和測量接點的傳熱方程,3個方程聯立求解可以得到測量接點溫度隨時間的變化。

測量接點、絕緣層、保護管層的傳熱方程分別為:

h1A1[T2(t)-T1(t)]+h2A2[T2(t)-T3(t)]=

h2A2[T3(t)-T2(t)]+h3A3[T3(t)-T4(t)]=

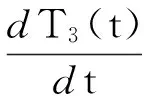
初始條件為:

T1(0)=T0

T2(0)=T0

T3(0)=T0

式中:h1為測量接點與保護管內壁之間的接觸系數,h2為保護管外壁面與被測介質之間的換熱系數,單位為W/(m2·K);A1為測量接點與絕緣層之間的換熱面積,A2絕緣層與保護管內壁之間的換熱面積,A3為保護管外壁與被測介質之間的換熱面積,單位為m2;T1(t)、T2(t)、T3(t)、T4(t)依次為測量接點、絕緣層、保護管、被測介質的溫度,單位為K;c1為測量接點比熱,c2為絕緣層比熱,c3為保護管比熱,單位為J/(kg·K);ρ1為測量接點密度,ρ2為絕緣層密度,ρ3為保護管密度,單位為kg/m3;V1為測量接點體積,V2為絕緣層體積,V3為保護管體積,單位為m3;t為時間,單位為s。

記:

Tb(t)=T1(t)-T0

Ti(t)=T2(t)-T0

Tm(t)=T3(t)-T0

Tg(t)=T4(t)-T0

并記:

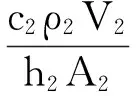
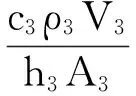
方程組變為:

聯立求解并做拉普拉斯變換,得到:

式(4)給出了絕緣式鎧裝熱電偶傳遞函數的結構及參數形式。

1.3 接殼式鎧裝熱電偶的雙集總熱容模型

接殼式鎧裝熱電偶的結構特征與絕緣式鎧裝熱電偶類似,但是測量接點和保護管端面內壁面直接接觸。類似式(4),接殼式鎧裝熱電偶雙集總熱容模型的傳遞函數為:

(5)

與絕緣式鎧裝熱電偶相比,接殼式鎧裝熱電偶的傳熱過程,不僅消除了絕緣層影響還消除了一個接觸熱阻。

1.4 簡化與降階

式(4)和式(5)表明,采用復合集總熱容法所建立的絕緣式鎧裝熱電偶模型是三階系統、接殼式鎧裝熱電偶模型是二階系統。當τ1、τ2和τ3較小時,鎧裝熱電偶傳熱過程可以被簡化為小時間常數慣性環節的串聯。以絕緣式鎧裝熱電偶為例,一種降階方法是直接把3個慣性環節合并為一個慣性環節,即:

式中:

τp1=τ1+τ2+τ3

另一種降階方法是忽略式(4)的高次項,即:

這兩種簡化方法都把傳熱過程簡化為一個整體上的一階慣性過程。但是從圖4所示意的傳熱過程分析,保護管、絕緣層和測量接點不僅構成一個小慣性群,保護管與絕緣層、絕緣層與測量接點之間還存在固有的接觸熱阻,并帶來溫度響應的兩次滯后。考慮到兩次滯后的疊加,降階方法可以是采用一階加延時系統,即:

(6)

與上述簡化過程類似,接殼式鎧裝熱電偶簡化后的傳遞函數也可以用式(6)表示。這兩種鎧裝熱電偶的傳遞函數可以統一表示為:

(7)

式(4)、式(5)和式(7)給出了鎧裝熱電偶傳遞函數的模型結構。當用實驗建模方法,對鎧裝熱電偶輸入輸出數據進行系統辨識時,這些模型結構可以作為先驗的傳遞函數結構。

2 實驗系統與實驗數據

2.1 實驗系統

為了獲得鎧裝熱電偶在實驗工況下的輸入輸出數據,采用雙槽法建立了實驗系統。其示意圖如圖5所示,主要包括計算機、數據采集卡(MCC-USB-2408)、可編程控制器(OmronCPM1A)、機械往復運動機構、激光對射開關(M12NPN)和兩個恒溫槽,其中一個恒溫槽配置為低溫槽,另一個配置為高溫槽。實驗主要環節包括,可編程控制器控制機械往復運動機構,驅動鎧裝熱電偶進出低溫槽和高溫槽,激光對射開關記錄鎧裝熱電偶與恒溫槽中介質發生接觸的時間點,數據采集卡記錄鎧裝熱電偶的輸出信號。

圖5 實驗系統示意圖

對鎧裝熱電偶做靜態響應標定后,用上述實驗系統測量鎧裝熱電偶在正負溫度階躍激勵下的輸入和輸出數據。實驗步驟參考溫度傳感器動態響應校準規程,實驗溫度區間設置為室溫到95 ℃。

2.2 實驗數據

圖6給出NR-81530快響應鎧裝熱電偶在正負溫度階躍激勵下的一組實驗數據。這種快響應鎧裝熱電偶的τ1、τ2和τ3的理論值都比較小,因此其傳遞函數可近似使用式(7)。圖6中輸入輸出數據的采樣時間為0.02s,數據長度為2 500。輸入和輸出數據處理為無量綱溫度。

圖6 NR-81530鎧裝熱電偶輸入和輸出

3 誤差模型與參數估計

當鎧裝熱電偶傳遞函數作為辨識對象時,對鎧裝熱電偶計算模型與傳熱過程之間的誤差做度量,可以采用輸出誤差模型或者方程誤差模型[20]。采用雙槽法做實驗,PLC驅動鎧裝熱電偶從低溫槽進入高溫槽,從高溫槽進入低溫槽,環境溫度對于輸入溫度和輸出溫度都存在影響。為此,選用輸出誤差類模型中的自回歸滑動平均模型也就是Box-Jenkins誤差模型,以便在計算模型中也能夠給出環境溫度等噪聲的估計[21]。

圖7 Box-Jenkins誤差模型

3.1Box-Jenkins誤差模型

對于輸出誤差類模型,自回歸滑動平均模型即Box-Jenkins模型的基本方程為:

(8)

模型示意圖如圖7所示。

圖7中,y(t)為鎧裝熱電偶輸出溫度序列,u(t)為輸入溫度序列,v(t)為噪聲序列,A(z)、B(z)、C(z)和D(z)是單位后移算子z-1的多項式,且:

A(z)=1+a1z-1+a2z-2+…+anaz-na

B(z)=b1z-1+b2z-2+…+bnbz-nb

C(z)=1+c1z-1+C2z-2+…+cncz-nc

D(z)=d1z-1+d2z-2+…+dndz-nd

另外,圖7中x(t)是中間變量,w(t)是噪聲項,且有:

定義θ為鎧裝熱電偶傳遞函數的待估計參數向量:

并定義φ為數據向量:

式中:φs(t)=[-x(t-1),-x(t-2),…,-x(t-na),u(t-1),u(t-2),…,u(t-nb)]T,φn(t)=[-w(t-1),w(t-2),…-w(t-nc),v(t-1),v(t-2),…,v(t-nd)]T。

則有:

于是式(8)可以寫成:

也就是:

y(t)=φT(t)θ+v(t)

(9)

上述模型構成一個偽線性回歸模型[22],數據向量φ中包含未知中間變量x(t-i)、噪聲項w(t-i)和v(t-i)。

3.2 準則函數與最小二乘迭代

考慮在實驗工況下,對鎧裝熱電偶輸入輸出數據做有限數據長度的離線辨識,并定義:

Y(t)=[y(t),y(t-1),…,y(1)]T

Φ(t)=[φT(t),φT(t-1),…φT(1)]T

V(t)=[v(t),V(t-1),…,v(1)]T

對于式(9)所表示的Box-Jenkins誤差模型,有:

Y(t)=Φ(t)θ+V(t)

(10)

如果定義準則函數為:

J(θ)=‖Y(t)-Φ(t)θ‖2

再對準則函數J(θ)極小化,令J(θ)對θ的導數為零,得到待估計參數向量θ的最小二乘估計,并表示為:

(11)

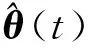
(12)

3.3 一階延時模型參數估計算例

模型輸出與實際輸出的比較如圖8所示,標準均方根誤差為79.19%。

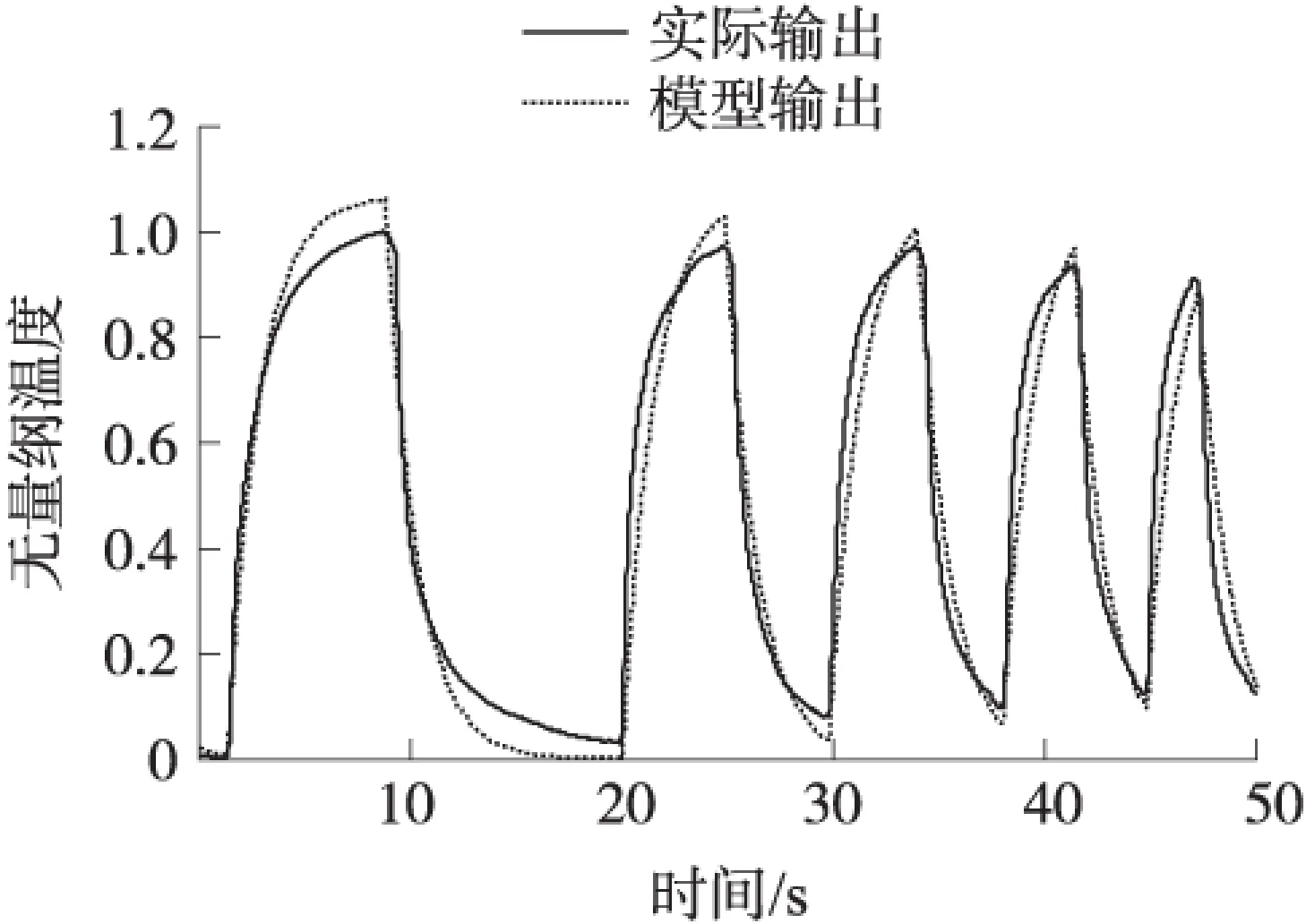
圖8 一階延時模型

3.4 一階延時加干擾模型參數估計算例

同樣是對于圖6中的實驗數據,考慮雙槽法實驗中環境溫度對測量數據的影響,采用Box-Jenkins模型,在一階延時模型中加入噪聲項,并估計其參數。迭代得到的傳遞函數為:

噪聲項的估計為:

模型輸出與實際輸出的比較如圖9所示,標準均方根誤差為82.95%,優于一階延時模型的辨識結果。

圖9 一階延時加干擾模型

4 結論

用理論建模和實驗建模結合的方法,分析了鎧裝熱電偶的動態響應特性。用Box-Jenkins誤差模型及最小二乘迭代方法計算了一種鎧裝熱電偶傳遞函數的參數。上述工作為評價鎧裝熱電偶動態特性提供了一種測試方法,也為熱電偶測量動態溫度時實驗建模及模型參數估計提供了一種非遞推辨識方法。

[1] Cherif Ould Lahoucinea,Abdallah Khellafb. Dynamic Characterization of a Thermocouple in a Fluid Crossflow[J]. Sensors and Actuators A:Physical,2005,119(1):48-56.

[2] 朱杰,郭濤. 一種Pt100溫度傳感器的動態熱響應模型[J]. 傳感技術學報,2013,26(1):73-77.

[3] 趙學敏,王文廉,李巖峰,等. 火焰溫度場測試中的傳感器動態響應研究[J]. 傳感技術學報,2016,29(3):368-372.

[4] Cherif Ould Lahoucinea,Abdallah Khellafb. Dynamic Characterization of a Transient Surface Temperature Sensor[J]. Procedia Engineering,2015(120):1245-1248.

[5] 高愛民,殳建軍,于國強,等. PT100熱電阻動態特性試驗研究與分析[J]. 傳感技術學報,2016,29(9):1395-1399.

[6] Vijaykumar Sathyamurthi,Debjyoti Banerjee. Non-linear Dynamical Analyses of Transient Surface Temperature Fluctuations during Subcooled Pool Boiling on a Horizontal Disk[J]. International Journal of Heat and Mass Transfer,2009,52:5608-5623.

[7] 楊永軍,蔡靜. 特殊條件下的溫度測量[M]. 北京:中國計量出版社,2009:148-150.

[8] Sarantis Pantazis,Joachim Buthig,Karl Jousten. Conjugate Heat Transfer Simulations of a Thermocouple Sensor in a Low Temperature Nitrogen Gas Ambient[J]. International Journal of Heat and Mass Transfer,2014,70:536-544.

[9] 溫淑慧,劉秀紅. 提高熱電偶動態測溫精度方法的研究[J]. 傳感技術學報,2004,27(1):175-178.

[10] 吳德會,趙偉,黃松嶺,等. 傳感器動態建模FLANN方法改進研究[J]. 儀器儀表學報,2009,30(2):362-367.

[11] 張朝龍,江巨浪,李彥梅,等. 基于云粒子群-最小二乘支持向量機的傳感器溫度補償[J]. 傳感技術學報,2012,25(4):472-477.

[12] 張平,宣益民,李強. 界面接觸熱阻的研究進展[J]. 化工學報,2012,63(2):335-349.

[13] 吳朋,林濤. 基于QGA_SVM的鎧裝熱電偶傳感器辨識建模研究[J]. 儀器儀表學報,2014,35(2):343-349.

[14] 王樂一,趙文虓. 系統辨識:新的模式、挑戰及機遇[J]. 自動化學報,2013,39(7):934-942.

[15] 王曉娜,于方舟,楊遂軍,等. 基于集總熱容法的薄膜熱電偶動態特性研究[J]. 傳感技術學報,2014,27(12):1627-1631.

[16] 盛煥行. 傳感器時間常數隨堆測定法[J]. 核動力工程,1984,5(2):71-83.

[17] 顧樵. 數學物理方法[M]. 北京:科學出版社,2012:104-107.

[18] Ahmed A Y AlWaaly,Manosh C Paul,Phillip S Dobson. Effects of Thermocouple Electrical Insulation on the Measurement[J]. Applied Thermal Engineering,2015,89:321-431.

[19] 王瑋. 微腔型PCR芯片的多體系集總熱容法分析[J]. 工程熱物理學報,2004,25(2):308-310.

[20] Isermann R,Munchhof M. 動態系統辨識[M]. 北京:機械工業出版社,2016:9-11.

[21] 劉清,岳東. 一類有輸入噪聲擾動的逆系統無偏參數辨識算法研究[J]. 控制理論與應用,2009,26(9):1031-1034.

[22] 丁鋒. 輸出誤差系統的多新息辨識方法[J]. 南京信息工程大學學報,2015,7(6):481-503.

李文軍(1970-),男,副教授,從事熱工測量等相關技術的研究,liwenjun@cjlu.edu.cn。

Estimating Transfer Function Models for Sheathed Thermocouple*

LI Wenjun*,SUN Hongjian,ZHENG Yongjun

(College of Metrological Technology and Engineering,China Jiliang University,Hangzhou 310018,China)

This paper presents a method for evaluating the dynamic characteristics of sheathed thermocouple. Composite lumped heat capacitance model of the sheathed thermocouple is derived based on the method of lumped heat capacitance analysis. Sheathed thermocouple heat transfer process includes protecting tube heat transfer,insulating layer heat transfer and hot junction heat transfer. The process is described as a series of three inertial element with lag. Thermal contact resistance is significant between protecting tube and insulating layer. A temperature drop is observed at the interface between the two surfaces in contact. Similar situations occur between insulating layer and hot junction. When the constant time of protection tube and the constant time of insulation are small,the transfer function of a sheathed thermocouple is simplified to be a first order process with delay. Based on the double thermostatic bath device,a bidirectional step temperature experiment system is established. The arrangement,in response to the changes in the temperature of the two thermostatic bath,provides input and output signals of the sheathed thermocouple. Two cases for the response of a thermocouple are reported,the first case concerns the response to a step perturbation,while the second deals with the response to a step perturbation with disturbance. Parameters are estimated by using computation algorithms to arrive at coefficients that best fit the selected auto regressive moving average model. Experiments are carried out and results prove that auto regressive moving average model is feasible for off-line identification of sheathed thermocouple.

sheathed thermocouple;lumped capacitance;transform function;auto regressive moving average

項目來源:國家科技重大專項項目(2015ZX02101)

2016-12-30 修改日期:2017-02-17

TP212.11

A

1004-1699(2017)07-1044-06

C:7230

10.3969/j.issn.1004-1699.2017.07.013