基于參數(shù)優(yōu)化MPE與FCM的滾動(dòng)軸承故障診斷

陳東寧，張運(yùn)東，姚成玉，來博文，呂世君

(燕山大學(xué) a．河北省重型機(jī)械流體動(dòng)力傳輸與控制實(shí)驗(yàn)室；b．先進(jìn)鍛壓成形技術(shù)與科學(xué)教育部重點(diǎn)實(shí)驗(yàn)室；c．河北省工業(yè)計(jì)算機(jī)控制工程重點(diǎn)實(shí)驗(yàn)室，河北 秦皇島，066004)

滾動(dòng)軸承是旋轉(zhuǎn)機(jī)械中應(yīng)用最廣泛，也是最容易出現(xiàn)故障的核心零部件。當(dāng)軸承出現(xiàn)異常或發(fā)生故障時(shí)，采集到的振動(dòng)信號(hào)往往具有非線性、非平穩(wěn)特征，而外界干擾噪聲則導(dǎo)致該信號(hào)的信噪比很低，故障特征難以提取[1]。因此，傳統(tǒng)的線性理論在滾動(dòng)軸承振動(dòng)信號(hào)分析的應(yīng)用中存在一定的局限性。

排列熵(Permutation Entropy, PE)是一種檢測(cè)一維時(shí)間序列復(fù)雜度的平均熵參數(shù)[2]，對(duì)信號(hào)的變化具有較高的敏感性，且算法簡單，可以更好地檢測(cè)復(fù)雜系統(tǒng)的動(dòng)力學(xué)突變。排列熵只能檢測(cè)時(shí)間序列在單一尺度上的復(fù)雜性和隨機(jī)性，復(fù)雜系統(tǒng)的輸出時(shí)間序列則在多重尺度上包含特征信息，為研究時(shí)間序列的多尺度復(fù)雜性變化，在排列熵的基礎(chǔ)上提出了多尺度排列熵(Multi-Scale Permutation Entropy, MPE)算法[3]，并在故障識(shí)別領(lǐng)域得到了很多應(yīng)用[4-6]。然而，多尺度排列熵算法的結(jié)果受自身參數(shù)的影響，若參數(shù)設(shè)置不合理，將無法達(dá)到最佳的處理效果。文獻(xiàn)[7]提出了基于重構(gòu)時(shí)間序列的最佳相空間來確定排列熵參數(shù)的方法，對(duì)嵌入維數(shù)和延遲時(shí)間的確定方法進(jìn)行了研究，但忽略了時(shí)間序列長度。目前，多尺度排列熵尺度因子與時(shí)間序列長度的選擇仍然僅憑經(jīng)驗(yàn)，如采用限定的幾個(gè)經(jīng)驗(yàn)數(shù)據(jù)長度值，通過觀察不同長度的高斯白噪聲的排列熵值確定時(shí)間序列長度[4]，此種方法雖能達(dá)到一定的處理效果，但所給定數(shù)據(jù)長度值的個(gè)數(shù)有限，且數(shù)值相差較大，難以準(zhǔn)確反映原始信號(hào)的特征信息。

也有學(xué)者保持多尺度排列熵算法中的某一個(gè)或某幾個(gè)影響參數(shù)不變，討論剩余的其他參數(shù)對(duì)處理結(jié)果的影響，但其忽略了參數(shù)之間的交互作用。因此，綜合考慮參數(shù)之間的交互影響，分別采用遺傳算法[8]和微粒群算法[9]對(duì)多尺度排列熵的參數(shù)進(jìn)行優(yōu)化，通過對(duì)比分析確定多尺度排列熵的最優(yōu)參數(shù)，提高算法的準(zhǔn)確性；進(jìn)而，提出以多尺度排列熵值作為特征參數(shù)、結(jié)合模糊C均值(Fuzzy C-Means Clustering，F(xiàn)CM)聚類算法[10]進(jìn)行模式識(shí)別的滾動(dòng)軸承故障診斷方法。

1 多尺度排列熵參數(shù)優(yōu)化

1.1 多尺度排列熵

多尺度排列熵定義為時(shí)間序列在不同尺度下的排列熵。對(duì)時(shí)間序列{X(i),i=1,2,…,N}進(jìn)行粗粒化處理，得到粗粒化序列

(1)

式中：N為時(shí)間序列的長度；[N/s]表示對(duì)N/s取整；s為尺度因子，s=1,2,…。當(dāng)s=1時(shí)，粗粒化序列為原始序列。分別計(jì)算每個(gè)粗粒化序列的排列熵即可得到時(shí)間序列的多尺度排列熵[3-7]。

在粗粒化環(huán)節(jié)中，尺度因子s的選擇尤為重要，若s取值過小，不能最大限度的提取信號(hào)的特征信息；若s取值過大，將有可能造成信號(hào)之間的復(fù)雜度差異被抹除。同時(shí)，在多尺度排列熵的計(jì)算過程中，若嵌入維數(shù)m取值太小，算法的突變檢測(cè)性能降低；若m取值太大，將無法反應(yīng)時(shí)間序列的細(xì)微變化。而且，時(shí)間序列長度N與延遲時(shí)間τ對(duì)多尺度排列熵算法也有不同的影響。可見，多尺度排列熵算法的參數(shù)設(shè)置影響其最終處理結(jié)果。因此，有必要對(duì)多尺度排列熵的參數(shù)進(jìn)行優(yōu)化。

1.2 遺傳算法參數(shù)優(yōu)化

遺傳算法是一種全局優(yōu)化的自適應(yīng)概率搜索算法，其借鑒了生物的自然選擇和遺傳進(jìn)化機(jī)制，適用于參數(shù)的選擇和優(yōu)化。利用遺傳算法對(duì)多尺度排列熵參數(shù)優(yōu)化的流程如圖1所示，其具體實(shí)現(xiàn)過程為：1)將優(yōu)化參數(shù)按二進(jìn)制進(jìn)行編碼；2)根據(jù)個(gè)體對(duì)目標(biāo)函數(shù)的適應(yīng)情況，選擇適應(yīng)度高的個(gè)體，淘汰適應(yīng)度低的個(gè)體；3)交叉、變異操作產(chǎn)生新的個(gè)體。若遺傳算法進(jìn)化達(dá)到最大進(jìn)化代數(shù)或連續(xù)幾代的適應(yīng)度沒有明顯的變化，則停止進(jìn)化。否則，重復(fù)以上過程繼續(xù)進(jìn)化。

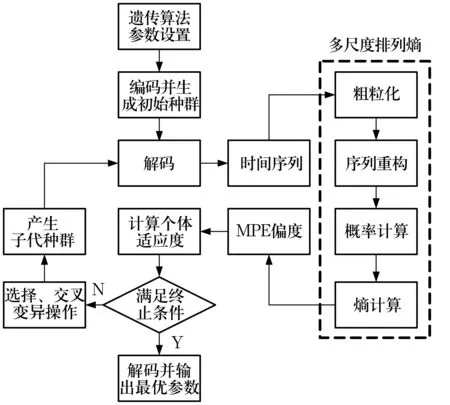
圖1 基于遺傳算法的多尺度排列熵參數(shù)優(yōu)化流程Fig.1 Procedure of MPE parameter optimization based on GA

適應(yīng)度函數(shù)是用于區(qū)分群體中個(gè)體好壞的標(biāo)準(zhǔn)，根據(jù)目標(biāo)函數(shù)變換得到。一般通過求取均值分析一組數(shù)據(jù)的總體趨勢(shì)，但僅憑均值并不能完全表征一組數(shù)據(jù)的總體概況，此時(shí)可求取數(shù)據(jù)的偏度。偏度越大，均值的效能越有問題；偏度越小，均值越可信賴[11]。因此，選用多尺度排列熵的偏度作為適應(yīng)度函數(shù)。

將時(shí)間序列X(i)所有尺度下的排列熵組成序列Hp(X)={Hp(1),Hp(2), …,Hp(s)}，計(jì)算其偏度Ske，得到適應(yīng)度函數(shù)，即

(2)

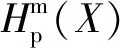
1.3 微粒群算法參數(shù)優(yōu)化

微粒群算法是一種高效的群體智能優(yōu)化算法，常被應(yīng)用于求解各種優(yōu)化問題。微粒群算法進(jìn)化時(shí)，每個(gè)微粒的速度與位置不斷被更新，其更新方程分別為

vid(t+1)=c1r1[pid(t)-xid(t)]+

c2r2[pgd(t)-xid(t)]+wvid(t)，

(3)

xid(t+1)=xid(t)+vid(t+1)，

(4)

式中：vid(t+1)，vid(t)分別為微粒i第t+1代和第t代的第d維的速度；xid(t+1)，xid(t)分別為微粒i第t+1代和第t代的第d維的位置；pid(t)為微粒i第t代個(gè)體最優(yōu)解的第d維；pgd(t)為第t代全局最優(yōu)解的第d維；w為慣性權(quán)重；c1，c2為加速常數(shù)；r1，r2為0～1之間相互獨(dú)立的隨機(jī)數(shù)。

利用微粒群算法搜尋多尺度排列熵參數(shù)的最優(yōu)解時(shí)，同樣設(shè)定適應(yīng)度函數(shù)為多尺度排列熵的偏度計(jì)算公式。基于微粒群算法的參數(shù)優(yōu)化流程如圖2所示，具體實(shí)現(xiàn)步驟如下：

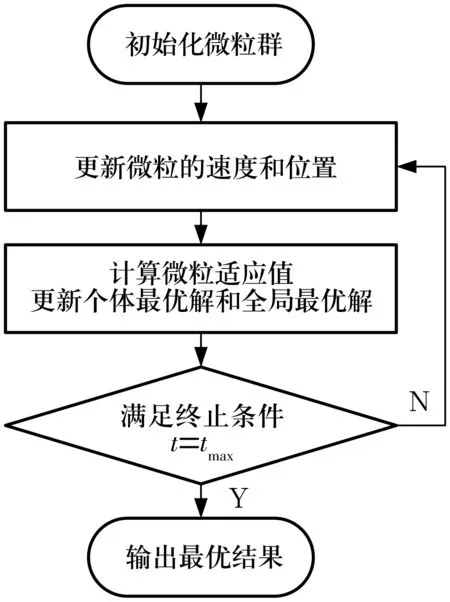
圖2 基于微粒群算法的多尺度排列熵參數(shù)優(yōu)化流程Fig.2 Procedure of MPE parameter optimization based on PSO

1)初始化微粒群，隨機(jī)初始化每個(gè)微粒每一維的速度與位置;

2)分別由(3)式和(4)式更新微粒的速度與位置;

3)根據(jù)(2)式，即多尺度排列熵的偏度公式計(jì)算微粒的適應(yīng)度，更新任意微粒的個(gè)體最優(yōu)解和全局最優(yōu)解;

4)判斷終止條件，若t=tmax，則執(zhí)行步驟5)，否則返回步驟2);

5)輸出優(yōu)化結(jié)果。

2 基于參數(shù)優(yōu)化MPE與FCM算法的故障診斷方法

多尺度排列熵可以度量信號(hào)在不同尺度下的復(fù)雜度，用多尺度排列熵量化軸承振動(dòng)信號(hào)并將多尺度排列熵值作為特征參數(shù)，可提取軸承故障特征。但滾動(dòng)軸承從正常狀態(tài)到發(fā)生故障是一個(gè)漸變的過程，只用特征值辨識(shí)不同類型或不同損傷程度的故障具有一定的難度。

模糊C均值算法是經(jīng)典的基于目標(biāo)函數(shù)的聚類算法，其通過極小化所有數(shù)據(jù)點(diǎn)與各聚類中心的歐氏距離及模糊隸屬度的加權(quán)和，不斷地迭代修正聚類中心和隸屬矩陣，直到符合終止準(zhǔn)則，將具有相似特性的數(shù)據(jù)樣本聚為一類，具體實(shí)現(xiàn)過程可參考文獻(xiàn)[10, 12]。因此，提出基于參數(shù)優(yōu)化多尺度排列熵與模糊C均值聚類相結(jié)合的故障診斷方法，診斷流程如圖3所示，具體步驟如下：

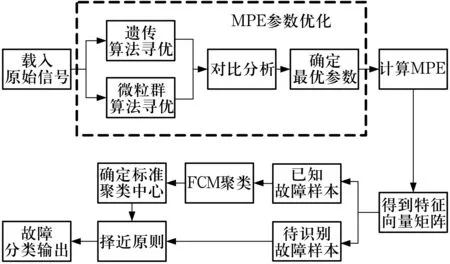
圖3 故障診斷流程Fig.3 Procedure of fault diagnosis

1)分別利用遺傳算法和微粒群算法對(duì)多尺度排列熵的參數(shù)進(jìn)行優(yōu)化，得到2組優(yōu)化參數(shù)。通過對(duì)比分析，確定多尺度排列熵的最優(yōu)參數(shù)組合;

2)將優(yōu)化得到的最優(yōu)參數(shù)組合重新設(shè)置為多尺度排列熵的參數(shù)，計(jì)算原始信號(hào)的多尺度排列熵值并進(jìn)行分析;

3)由得到的多尺度排列熵值提取合適的特征向量，選取一部分作為已知故障樣本，另一部分作為待識(shí)別故障樣本。利用模糊C均值聚類算法確定已知故障樣本的標(biāo)準(zhǔn)聚類中心，由擇近原則計(jì)算待識(shí)別故障樣與標(biāo)準(zhǔn)聚類中心的距離，實(shí)現(xiàn)滾動(dòng)軸承的故障分類識(shí)別。

3 實(shí)例分析

采用美國凱斯西儲(chǔ)大學(xué)電氣工程實(shí)驗(yàn)室的滾動(dòng)軸承試驗(yàn)數(shù)據(jù)進(jìn)行分析。測(cè)試驅(qū)動(dòng)端軸承為6205-2RS JEM SKF深溝球軸承，采用電火花加工技術(shù)在軸承上布置單點(diǎn)故障，通過安裝在電動(dòng)機(jī)驅(qū)動(dòng)端軸承座上方的加速度傳感器采集軸承的振動(dòng)加速度信號(hào)。

3.1 多尺度排列熵參數(shù)優(yōu)化

選取電動(dòng)機(jī)轉(zhuǎn)速為1 750 r/min時(shí)軸承正常狀態(tài)下的振動(dòng)信號(hào)數(shù)據(jù)，分別利用遺傳算法與微粒群算法優(yōu)化多尺度排列熵的參數(shù)，優(yōu)化結(jié)果見表1，微粒群算法全局最優(yōu)適應(yīng)度隨進(jìn)化代數(shù)的變化曲線如圖4所示。

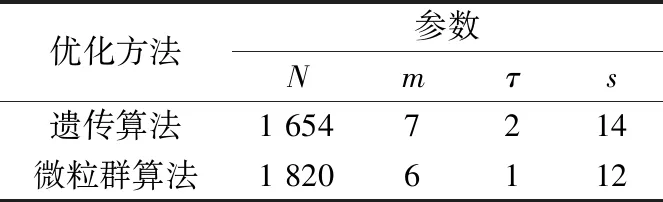
表1 多尺度排列熵參數(shù)優(yōu)化結(jié)果Tab.1 Results of MPE parameters optimization

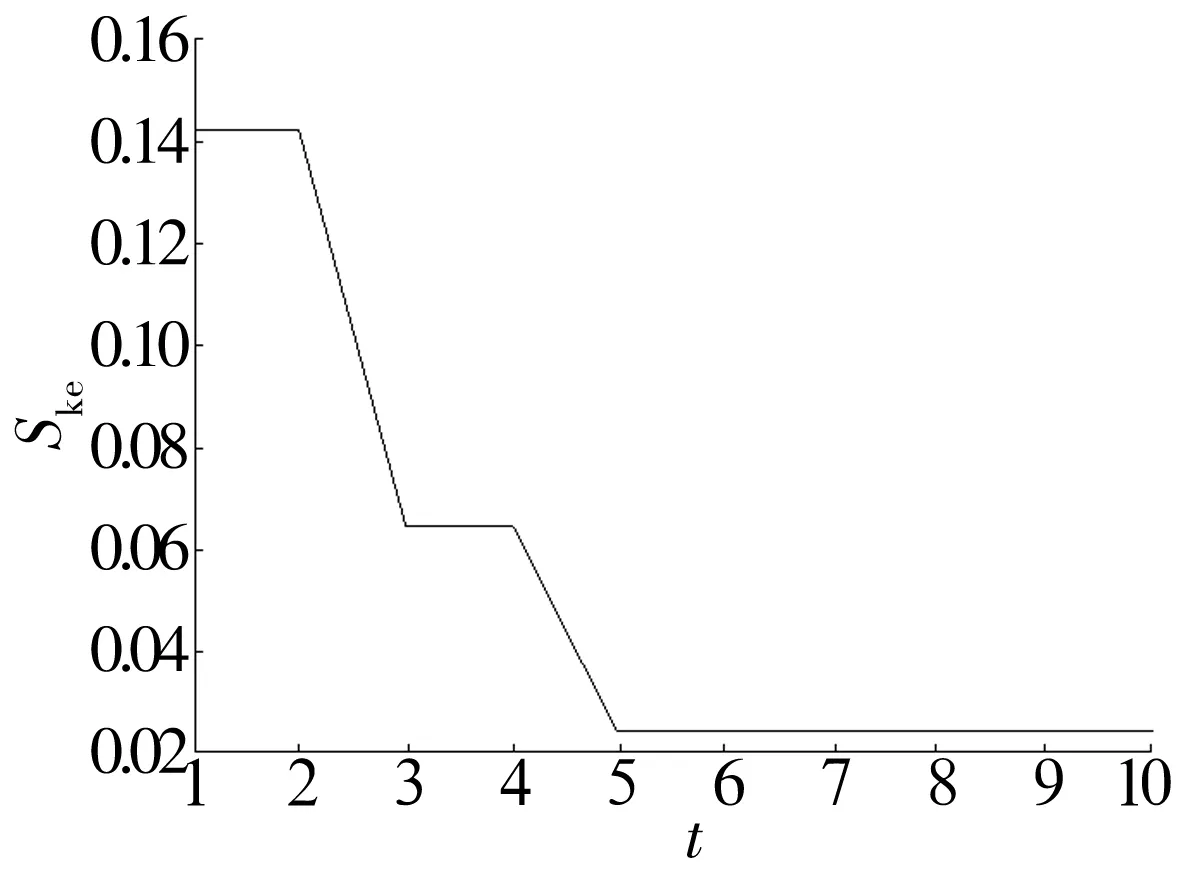
圖4 全局最優(yōu)適應(yīng)度隨進(jìn)化代數(shù)的變化

Fig.4 Variation of global optimal fitness with evolutionary generations

為確定多尺度排列熵的最優(yōu)參數(shù)組合，用模糊C均值聚類的聚類效果對(duì)2組參數(shù)進(jìn)行對(duì)比，聚類效果可用分類系數(shù)F和平均模糊熵H進(jìn)行檢驗(yàn)，分別為

(5)

(6)

式中：c為聚類中心個(gè)數(shù)；n為樣本個(gè)數(shù)；uij為第j個(gè)樣本屬于第i類的隸屬度。分類系數(shù)越接近1，聚類效果越好；平均模糊熵越接近0，聚類效果越好。

分別設(shè)置2組優(yōu)化參數(shù)為多尺度排列熵的參數(shù)，選取軸承4種狀態(tài)的振動(dòng)信號(hào)數(shù)據(jù)各20組，分別計(jì)算這些信號(hào)的多尺度排列熵值，并將其作為特征向量輸入模糊C均值聚類分類器中，根據(jù)(5)式和(6)式分別計(jì)算2組優(yōu)化參數(shù)的分類系數(shù)和平均模糊熵。同時(shí)，為驗(yàn)證參數(shù)優(yōu)化的有效性，選取文獻(xiàn)[4]中參數(shù)以及一組經(jīng)驗(yàn)參數(shù)(N=2 048，m=5，τ=3，s=15)對(duì)其聚類效果進(jìn)行檢驗(yàn)，結(jié)果見表2。

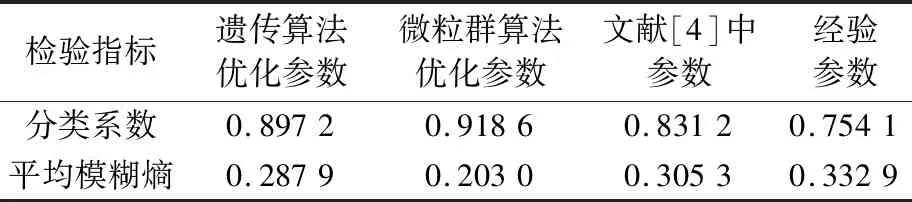
表2 優(yōu)化參數(shù)聚類效果檢驗(yàn)Tab.2 Clustering results of optimized parameters

由表2可知：與文獻(xiàn)[4]及經(jīng)驗(yàn)參數(shù)的結(jié)果相比，2種優(yōu)化參數(shù)的分類系數(shù)較大、平均模糊熵較小，說明優(yōu)化參數(shù)的聚類效果較好。經(jīng)微粒群算法優(yōu)化后，其分類系數(shù)更接近1，且平均模糊熵更接近0，所以，經(jīng)微粒群算法優(yōu)化后的參數(shù)聚類效果更好，故設(shè)置多尺度排列熵的參數(shù)為經(jīng)微粒群算法優(yōu)化后的參數(shù)。

3.2 同負(fù)荷下不同類型故障的診斷

選取電動(dòng)機(jī)負(fù)荷2 HP，電動(dòng)機(jī)轉(zhuǎn)速為1 750 r/min時(shí)軸承正常、內(nèi)圈故障、外圈故障和鋼球故障4種狀態(tài)下的振動(dòng)信號(hào)進(jìn)行分析，4種狀態(tài)振動(dòng)信號(hào)的局部時(shí)域圖如圖5所示。采樣頻率為12 kHz，每種狀態(tài)取40組數(shù)據(jù)，每組數(shù)據(jù)長度均為1 820。前20組數(shù)據(jù)作為已知故障樣本，將其多尺度排列熵值作為特征向量輸入模糊C均值聚類分類器，求取已知故障的標(biāo)準(zhǔn)聚類中心，后20組數(shù)據(jù)作為待識(shí)別樣本，采用Euclid貼近度的擇近原則對(duì)滾動(dòng)軸承各種故障進(jìn)行識(shí)別。

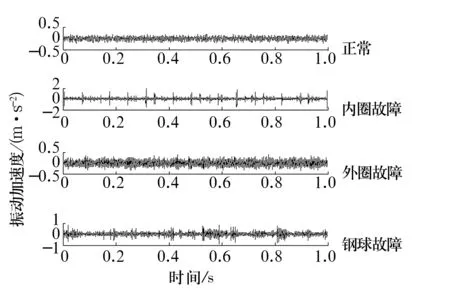
圖5 滾動(dòng)軸承不同狀態(tài)下振動(dòng)信號(hào)的時(shí)域圖Fig.5 Time domain of rolling bearing vibration signals under different states

將待識(shí)別樣本A與標(biāo)準(zhǔn)聚類中心O組成故障診斷集B={b1,b2,…,bz}，z為B中樣本個(gè)數(shù)，則A與O的Euclid貼近度δ(A,O)為

(7)

式中：A(bi)，O(bi)分別為A與O的隸屬度函數(shù)。

當(dāng)軸承發(fā)生故障時(shí)，其振動(dòng)特性發(fā)生改變，主要體現(xiàn)在幅值和周期特性上，但時(shí)域圖所能獲取的信息量較少。對(duì)軸承4種狀態(tài)的振動(dòng)信號(hào)進(jìn)行多尺度排列熵分析，計(jì)算得到多尺度排列熵如圖6所示。從圖6可以看出，不同狀態(tài)的滾動(dòng)軸承多尺度排列熵值不同，這是因?yàn)楫?dāng)滾動(dòng)軸承發(fā)生故障時(shí)，振動(dòng)信號(hào)的隨機(jī)性發(fā)生變化，使排列熵值發(fā)生變化。在同一狀態(tài)下，隨尺度增大，粗粒化序列的隨機(jī)性和復(fù)雜性降低，排列熵值的變化幅度減小。

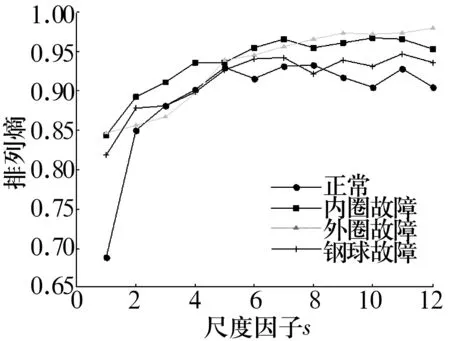
圖6 滾動(dòng)軸承不同狀態(tài)下振動(dòng)信號(hào)的多尺度排列熵Fig.6 MPE of rolling bearing vibration signals under different states

然而，圖6仍不能明顯區(qū)分滾動(dòng)軸承的4種狀態(tài)，故提出以參數(shù)優(yōu)化多尺度排列熵值作為特征參數(shù)，結(jié)合模糊C均值聚類算法對(duì)滾動(dòng)軸承故障進(jìn)行識(shí)別分類。計(jì)算滾動(dòng)軸承4種狀態(tài)各40組數(shù)據(jù)樣本的多尺度排列熵值，并選取每種狀態(tài)前20組數(shù)據(jù)的多尺度排列熵值進(jìn)行訓(xùn)練；最后，選取表征振動(dòng)信號(hào)主要信息的前5個(gè)尺度的排列熵值作為特征向量，用模糊C均值算法對(duì)其進(jìn)行聚類分析，結(jié)果如圖7所示。

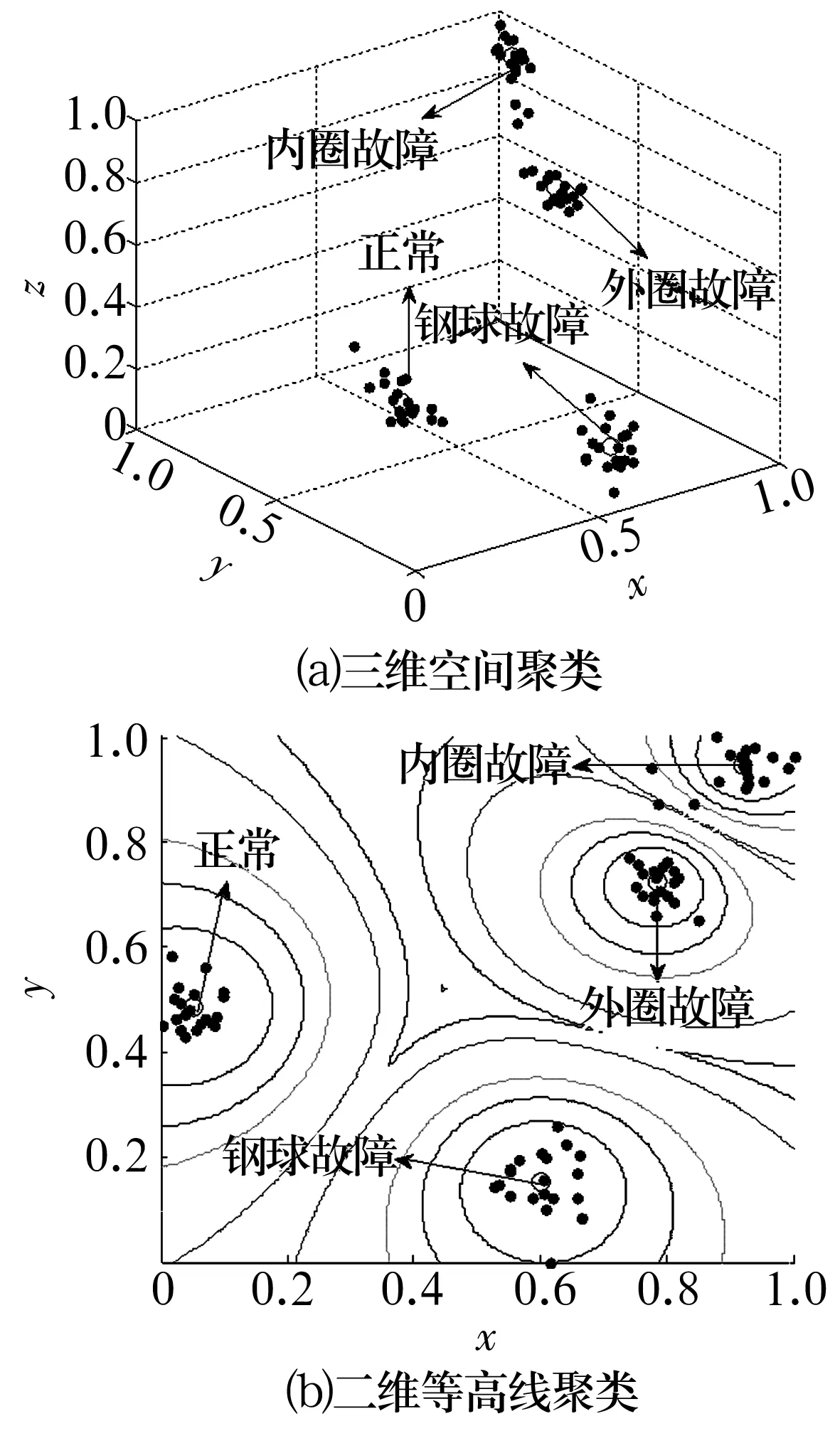
圖7 滾動(dòng)軸承不同狀態(tài)下振動(dòng)信號(hào)的聚類分析結(jié)果Fig.7 Cluster analysis results of rolling bearing vibration signals under different states

從圖7可以看出，80組樣本數(shù)據(jù)經(jīng)過模糊C均值聚類算法處理后，按照故障類型分布在4個(gè)聚類中心的周圍，說明基于參數(shù)優(yōu)化多尺度排列熵和模糊C均值聚類算法的故障診斷方法具有很好的分類識(shí)別效果。取分類得到的4個(gè)聚類中心為標(biāo)準(zhǔn)聚類中心，通過計(jì)算后20組待識(shí)別樣本的多尺度排列熵值與標(biāo)準(zhǔn)聚類中心的Euclid貼近度判斷滾動(dòng)軸承故障類型。

為進(jìn)一步驗(yàn)證上述方法的有效性，分別以單一尺度排列熵和樣本熵進(jìn)行對(duì)比分析。依據(jù)同樣的原理，通過分別計(jì)算待識(shí)別樣本的排列熵、樣本熵與標(biāo)準(zhǔn)聚類中心的Euclid貼近度判斷軸承故障類型。3種方法的診斷結(jié)果見表3。由表3可知：基于參數(shù)優(yōu)化多尺度排列熵與模糊C均值聚類的滾動(dòng)軸承故障識(shí)別率為100%，高于其他2種方法的故障識(shí)別率，且多尺度排列熵的分類系數(shù)、平均模糊熵均優(yōu)于單一尺度排列熵和樣本熵。

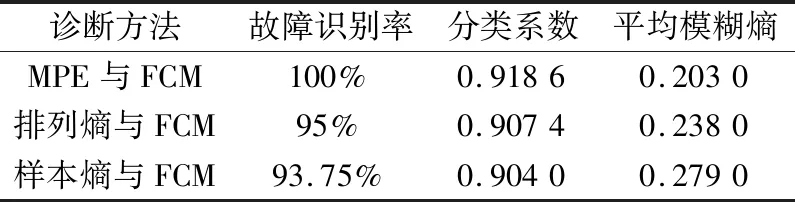
表3 不同類型故障的診斷結(jié)果Tab.3 Results of fault diagnosis in different types

3.3 同負(fù)荷下不同損傷程度故障診斷

選取電動(dòng)機(jī)負(fù)荷2 HP，電動(dòng)機(jī)轉(zhuǎn)速為1 750 r/min時(shí)軸承正常、內(nèi)圈輕微損傷和內(nèi)圈嚴(yán)重?fù)p傷3種故障類型進(jìn)行驗(yàn)證，其中，輕微損傷直徑為0.177 8 mm，嚴(yán)重?fù)p傷直徑為0.533 4 mm。

同樣，對(duì)不同損傷程度的軸承振動(dòng)信號(hào)分別選取40組數(shù)據(jù)，數(shù)據(jù)長度均為1 820，其多尺度排列熵和聚類分析結(jié)果分別如圖8、圖9所示。

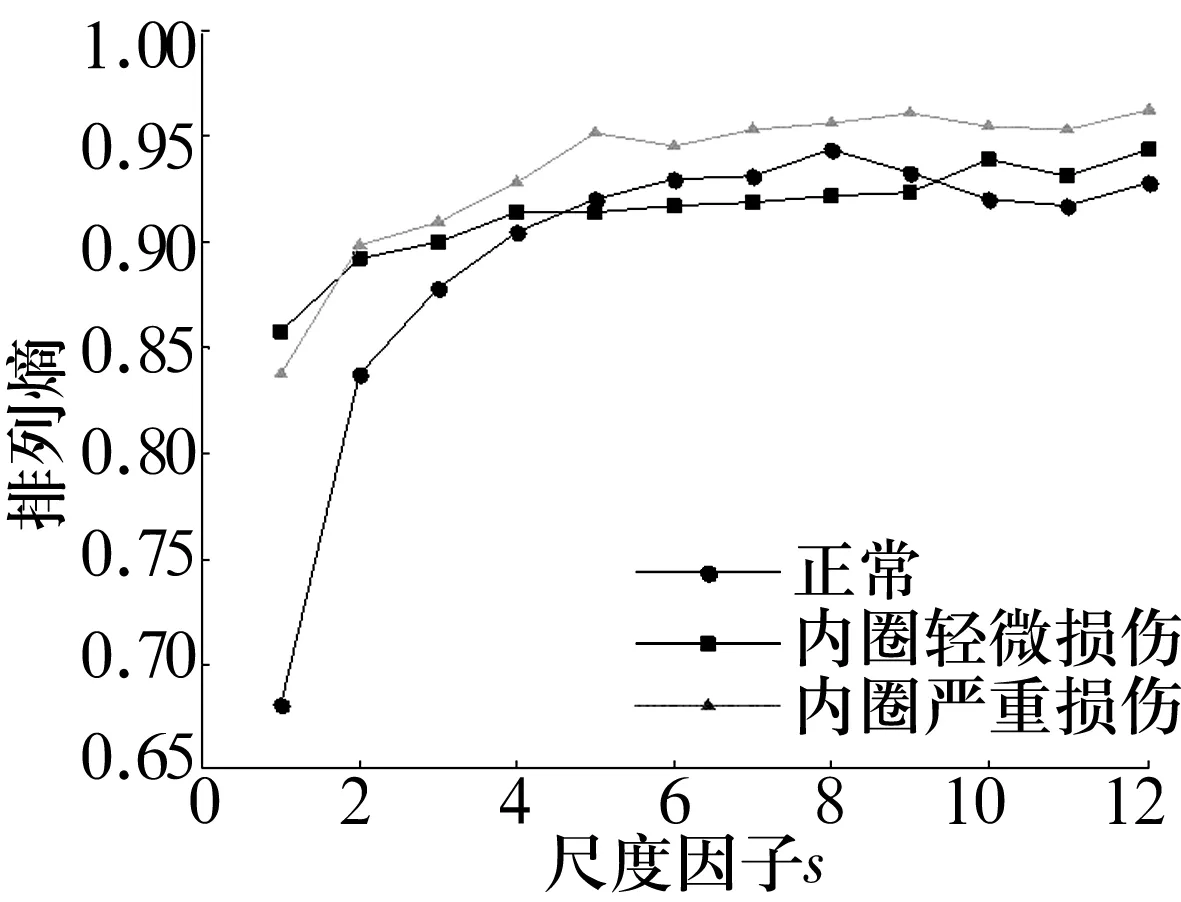
圖8 不同損傷程度多尺度排列熵Fig.8 MPE of different damage degree

從圖8可以看出，軸承正常與內(nèi)圈嚴(yán)重?fù)p傷故障區(qū)分較為明顯，軸承正常與內(nèi)圈輕微損傷、內(nèi)圈嚴(yán)重?fù)p傷與內(nèi)圈輕微損傷則不能明顯區(qū)分出來。而從圖9可以看出，經(jīng)模糊C均值聚類分類后，軸承不同損傷程度的故障被有效區(qū)分。同樣對(duì)上述3種方法進(jìn)行對(duì)比分析，結(jié)果見表4。由表4可知：在不同損傷程度的軸承故障診斷中，基于參數(shù)優(yōu)化多尺度排列熵與模糊C均值聚類方法的故障識(shí)別率仍優(yōu)于其他2種方法，而分類系數(shù)與平均模糊熵亦可證明該方法的優(yōu)越性。

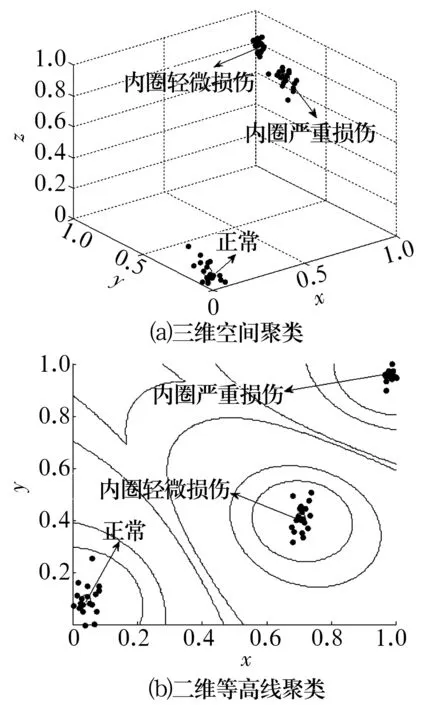
圖9 不同損傷程度軸承振動(dòng)信號(hào)的聚類分析結(jié)果Fig.9 Cluster analysis results of rolling bearing vibration signals in different damage degree

表4 不同損傷程度故障診斷結(jié)果Tab.4 Results of fault diagnosis in different damage degree

3.4 不同負(fù)荷下的故障診斷

在故障診斷的實(shí)際應(yīng)用中，獲得所有工況下的不同故障類型數(shù)據(jù)比較困難，因而利用已有工況故障數(shù)據(jù)識(shí)別其他工況的故障類型具有一定的實(shí)際意義。為此，利用電動(dòng)機(jī)負(fù)荷為2 HP時(shí)的標(biāo)準(zhǔn)聚類中心，對(duì)其他負(fù)荷工況進(jìn)行故障診斷，進(jìn)而評(píng)估該方法的適用性。

從負(fù)荷1 HP工況下抽取30組不同類型故障數(shù)據(jù)作為待識(shí)別樣本，通過計(jì)算與標(biāo)準(zhǔn)聚類中心的Euclid貼近度進(jìn)行故障識(shí)別，結(jié)果見表5。

由表5可知：參數(shù)優(yōu)化多尺度排列熵與模糊C均值聚類結(jié)合的診斷結(jié)果中只有內(nèi)圈故障與鋼球故障被錯(cuò)分，而其他2種方法除內(nèi)圈故障與鋼球故障容易被錯(cuò)分外，外圈故障也易被診斷為內(nèi)圈故障。這是由于變負(fù)荷下軸承故障信號(hào)發(fā)生明顯變化，導(dǎo)致變負(fù)荷下的故障識(shí)別率降低。而多尺度排列熵在引入尺度因子后，能夠從不同尺度上更好地反映軸承振動(dòng)信號(hào)的動(dòng)力學(xué)突變，豐富故障特征信息，在變負(fù)荷工況下仍可獲得較高的故障識(shí)別率，說明其具有很好的適用性。

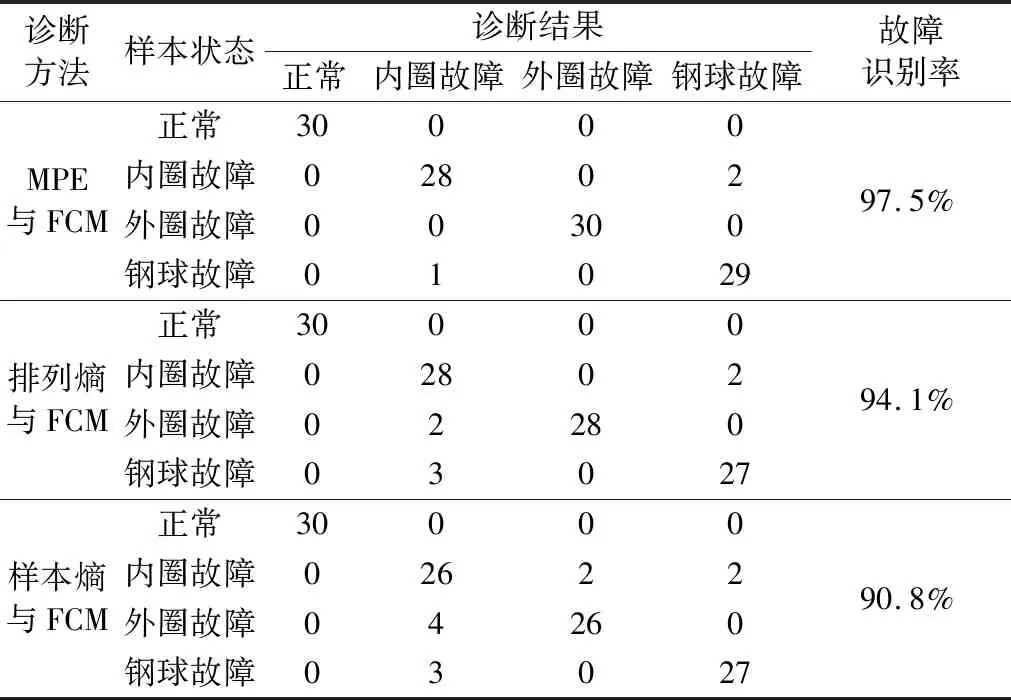
表5 負(fù)荷1 HP工況下不同故障類型診斷結(jié)果Tab.5 Results of fault diagnosis in different types under 1 HP load condition

4 結(jié)束語

針對(duì)多尺度排列熵算法的最佳參數(shù)確定問題，充分考慮參數(shù)之間的交互影響，以多尺度排列熵偏度作為適應(yīng)度函數(shù)，基于遺傳算法和微粒群算法綜合求解優(yōu)化多尺度排列熵的參數(shù)；進(jìn)而利用參數(shù)優(yōu)化多尺度排列熵對(duì)滾動(dòng)軸承振動(dòng)信號(hào)進(jìn)行特征提取，與未優(yōu)化參數(shù)的對(duì)比分析證明，參數(shù)優(yōu)化多尺度排列熵進(jìn)行特征提取具有更好的分類識(shí)別效果。

將參數(shù)優(yōu)化多尺度排列熵與模糊C均值聚類相結(jié)合，應(yīng)用于同負(fù)荷與變負(fù)荷工況下滾動(dòng)軸承的故障診斷，通過與單一尺度排列熵、樣本熵結(jié)合模糊C均值聚類的方法進(jìn)行對(duì)比，結(jié)果表明：上述方法在同負(fù)荷與變負(fù)荷工況下的故障識(shí)別率均高于后兩者，分類識(shí)別效果較好，為實(shí)際應(yīng)用中故障數(shù)據(jù)不完整情況下的故障診斷提供了一條有效途徑。