單純形方法中使用數形結合解析的幾個問題

蔡江波

【摘要】數學學科在現階段高職院校基礎性學科培養體系中處于重要的位置，它對于學生的基礎知識認知體系的形成具有重要意義.線性規劃方法是現代數學學科發展路徑中用于解決復雜線性約束條件下的最優解問題的基本方法，在現代數學的發展脈絡中具備極其深遠的現實影響意義.

【關鍵詞】高職數學；單純性方法；數形結合

單純形方法是現代數學中解決線性規劃最優解問題的基礎的和首要的應用方法，對于有效解決無最優解的線性規劃問題、退化解線性規劃問題，以及多重最優解的線性規劃問題，具備顯著的促進和保障作用.由于現階段絕大多數高職院校學生尚且無法做到對單純形方法求解現行規劃問題的本質能夠準確理解，因而，給實際教學效果造成了顯著的不良影響，而數形結合方法在實際教學中的引入和運用，為有效解決上述教學困境做出了重要貢獻.鑒于此，本文將會圍繞用數形結合解析單純形方法教學中的幾個問題展開簡要闡釋.

一、無最優解的線性規劃問題

在線性規劃數學問題的運算處理過程中，受所求問題和可行域便捷約束條件等因素的共同影響，通常會出現最優解不存在現象，而且針對這一數學問題的計算和證明，往往也是具體教學環節開展過程中的難點.

例1求解如下線性規劃問題：

maxS=3X1+2X2，其約束條件為X1-X2≤2.00；200X1-X2≤6.00；X1≥0；X2≥0.

解根據題干和已知條件，先將原有問題的表述語句轉化為標準形式，并同時引入松弛數學變量X3和X4，這時可以得到新的問題表達語句為maxS=3.00X1+2.00X2+0X3+0X4.其基本的數學規劃約束條件為X1-X2+X3=200；2.00X1-X2+X4≤6.00；X1≥0；X2≥0；X3≥0；X4≥0.

選取線性規劃數學運算條件下的可行基Bi=（P3，P4）=E，可以具體列示出線性規劃可行基B1在單純形線性規劃方法運用條件下的數值分布表，并借助換基迭代方法獲取如表1所示數據結果.

在線性規劃數學運算條件下的可行基Bi=（P1，P2）具體對應的單純形測算數據量表中，由于檢驗性控制參數（-Cj）項目中的（-7.00）數據項具有非正數屬性表現特征，因而，應當針對現有的非基變量項目（X3）實施進基運算處理，與此同時，由于非基變量項（X3）在這一運算處理條件下，所對應表格數據列中的（-1.00）和（-2.00）項均具有非正數的數學屬性特征，直接導致這一數學運算處理情境之下未能形成基變量處理項目，因而，可以確定這一線性規劃問題在現有的數學約束條件下不存在最優解求解結果.

以線性規劃問題求解活動的基本思路展開簡要分析，如果某一檢驗性參數所在單純形數據表的所在列向量中不存在數值表征屬性為正數的數據項，則直接可以判定，對應的數學線性規劃問題不存在最優解.

以例題1所列示的數學問題場景展開分析，基于初始化數據求解列表中的T（B1）數據列，即可明確實現對問題中最優解存在與否的準確判斷，由于檢驗性控制參數（-Cj）項目所在數據列中的（-2.00）<0，直接可知檢驗性控制參數（-Cj）項目所在的第二列數據元素中不存在具備正數數學屬性的數據項目，因而，導致例題1所列示的線性數學規劃問題，在現有的約束條件之下，不存在最優解.在此基礎上，本文將結合幾何圖形，對例題1的數學描述特征展開分析.

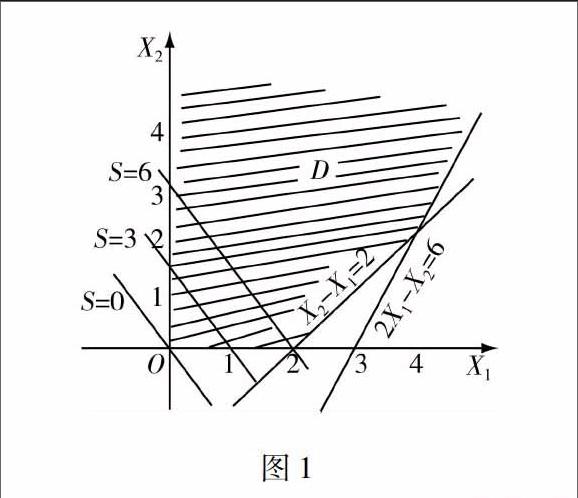
如圖1所示，由于在題干所述的初始性數學約束條件中，（X2）項的約束系數均為非正數，表明在現有的線性規劃數學條件之下，（X2）處于不受約束狀態，也就是說，例題1對應的可行域圖形具有無上界特征.與此同時，對于線性規劃問題求解過程中的目標直線簇S而言，其最優化求解過程中的方向，是沿著可行無上界域的上方呈現無限變化趨勢的，因而，可以在圖形分析背景下，證實例題1所述問題不存在最優解.

二、退化解線性規劃問題

例2求解如下線性規劃問題：

maxS=-2.00X1-5.00X2；其約束條件為X1+3.00X2≤6.00；X1-X2≤2.00；X1≥0；X2≥0.

解根據題干和已知條件，先將原有問題的表述語句轉化為標準形式，并同時引入松弛數學變量X3和X4，這時可以得到新的問題表達語句為maxS=2.00X1+5.00X2+0X3+0X4.

其基本的數學規劃約束條件為X1+3.00X2+X3=600；X1-X2+X4=2.00；X1≥0；X2≥0；X3≥0；X4≥0.

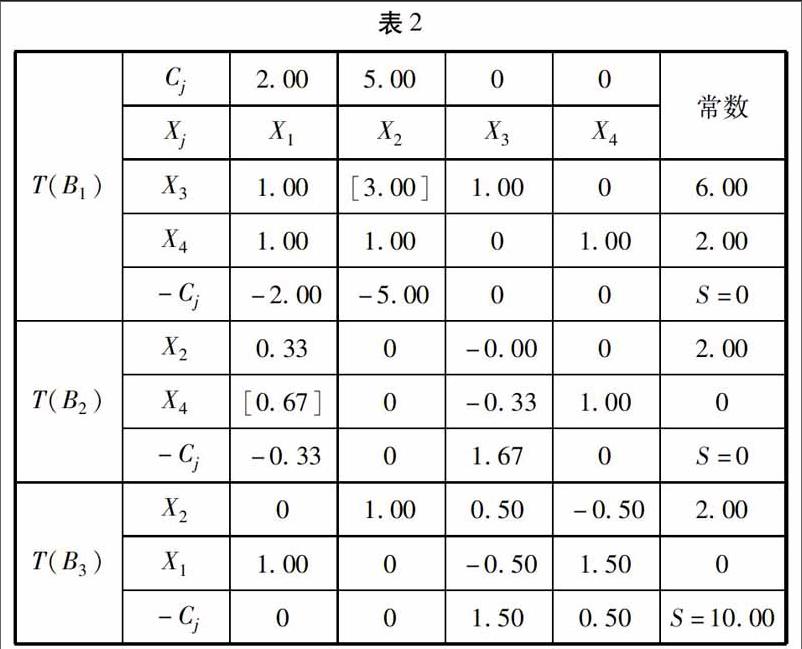
選取線性規劃數學運算條件下的可行基Bi=（P3，P4）=E，可以具體列示出線性規劃可行基B1在單純形線性規劃方法運用條件下的數值分布表，并借助換基迭代方法獲取如表2所示數據結果.

通過對基項參數T（B3）中列示的相關內容展開具體分析，可知例題2中所列線性規劃問題的最優解為S=-1000，此時X1=0，X2=2.00.

在實施第一次迭代運算處理過程中，如果在完成基變量項目選擇環節基礎上，同時出現了兩個具備等同性比值特征的最小值，則通常可以任意選取其中的一個作為后續運算處理過程中的基礎條件.如果在完成第一次迭代運算處理基礎上出現了基變量項目X1=0的運算處理結果，則通常認為這一運算條件下獲取的最優解，具備退化特征.

在實際開展基變量選取環節過程中，如果同時存在兩個或者是兩個以上的、具備等同性比值特征的最小值，如果在這一運算處理情境下，隨機選取任意一個最小值展開后續的進基性計算分析規劃求解處理過程中，往往會同時出現一個或者是多個基變量參數項目同時為零的運算處理結果，這時通常認為實際求解獲取的基礎解具備表征明顯的退化性特征.

在線性規劃問題的運算求解構成中，退化解計算結果的出現，將會直接導致目標函數無法獲取到及時有效的數學改良，因而，在運用一般運算法處理后獲取的新的線性規劃解，往往依然具有退化特征，直接導致線性規劃問題的求解處理過程，在有限的區間內呈現出循環往復特征，始終無法實現對最優解的求解處理目標.為切實解決退化解運算處理過程中的循環往復現象，通常需要：分別計算出緊接求解列之后一列的元素與求解列相應的元素的比值數據結果，并從中選取比值數據最小的一個數據行作為最終應用的求解行.

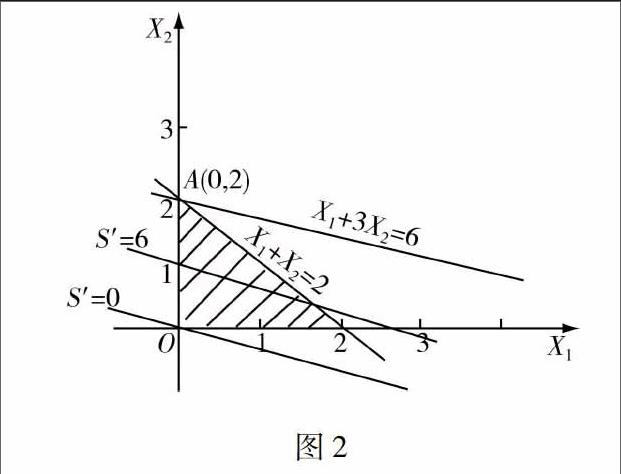
例題2中所列示數學情境，其具體涉及的運算求解處理過程，不具有循環性表現特征，直接導致該問題通過換基迭代的計算處理方法，能夠獲取到最優化的結果.在引入數形結合分析方法基礎上，可以獲取如圖2所示的可行域.

在圖2所示的可行域求解圖形中，A點對應的恰好就是基于單純形法獲取的基本解系，在單純形計算處理方法背景下所表現的變化特征.

事實上，在例題2所述的問題情境中，點A（0，2）在兩個獨立存在的線性規劃約束條件的共同約束之下，就可以實現準確的運算描述.而本組例題中同時給出了三個線性規劃可行域邊界約束條件，即X1=0；X1+X2=2.00；X1+3.00X2=6.00.從這里可以知道，在線性規劃可行域的便捷約束條件數量超過極點確定過程中的約束條件個數限制條件下，通常會導致線性規劃數學問題，在具體的求解處理過程中，出現退化解現象，給最優解的計算分析求解處理過程造成極其顯著的技術困難.

三、結束語

針對數形結合解析單純形方法教學中的幾個問題，本文從無最優解的線性規劃問題、退化解線性規劃問題兩個基本方面，結合對具體例題的計算分析處理，具體論述了線性規劃問題求解過程中最優解的不存在現象，以及可能發生的循環性退化解問題，旨在為相關領域的研究人員和一線教師提供借鑒.

【參考文獻】

[1]黎鐵新.用數形結合解析單純形方法教學中的幾個問題[J].高教論壇，2005（06）：151-153.

[2]茍愛章.數形結合在解題中的應用[J].數學教學研究，2013（09）：61-63.

[3]王東援，杜秀玲，冷福林.介紹一種最優化方法——單純形法[J].環境與健康雜志，1986（04）：20-22，25.