普拉圖和施泰納問題的實驗解法

潘偉云

【摘要】用含有給定的基本元素或公式明確地解出變分式的問題，通常是很困難的.此時，我們常常先證明在某種條件下解是存在的，然后再研究解的性質.當存在性變得困難時，人們就把數學問題看作是物理現象的解釋.這時物理現象的存在性就表示數學問題解的存在性.

【關鍵詞】普拉圖問題；施泰納問題；實驗解法

一、預備知識

定義[1]變分法：是處理函數變量的數學領域和處理數的函數的普通微積分.變分法最終尋找的是極值函數，它們使得泛函取得極大值或極小值.

二、極小問題的肥皂膜實驗

普拉圖問題[2]：在空間中給定一閉圍線，求以這條曲線為邊界，具有最小面積的曲面.

在數學上，普拉圖問題與偏微分方程組的解有關.歐拉指出，所有不是平面的極小曲面必是鞍形的，并且在每一點的平均曲率都是零.在20世紀，很多特殊情況證明了這類問題的解是存在的，到了20世紀末，才由道格拉斯（J.Douglas）和雷多（T.Rado）證明.

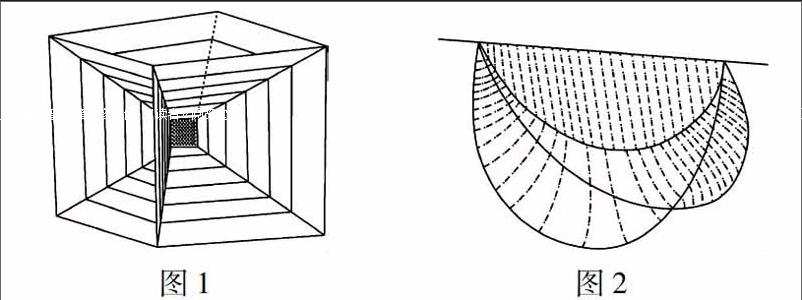
用普拉圖的實驗，對很一般的閉曲線可以立即得到物理解.如果人們把一個金屬絲做成的任意閉曲線，浸入表面張力較小的液體內，然后再提出來，那么繃在圍線上的膜就是具有最小面積的極小曲面.（假設我們可以忽略重力和其他干擾薄膜趨向具有最小面積的平衡位置的力，那么只需考慮表面張力所引起的最小位能值就可以了）這種液體的一種好配方如下：把10千克的純油酸鈉，溶于500克的蒸餾水中，再把15個立方單位的這種溶液和11個立方單位的甘油混合.用這種溶液在黃銅絲架上得到的膜比較穩定.這種框架的直徑不超過15厘米.用這種方法很容易“解”普拉圖問題，這只需將黃銅絲做成我們所需的形狀就可以了.由一系列正多面體的棱所構成的多邊形的黃銅絲框架上可以得到許多美麗的曲面.特別是把整個立方體框架浸在這種溶液中.更為有趣，最初的結果是，沿每條棱線，一系列不同的曲面彼此以120度的角相交（如果很小心地取出立方體框架，那么將有13個近乎平面的曲面，如圖1所示）.然后我們可以捅破許多這種不同的曲面，最后只剩一個邊界為一閉多邊形的曲面.對于四面體也可做同樣的實驗.

三、施泰納問題及其推廣的實驗

施泰納問題[4]：將三個村莊用總和長為極小的道路連接.

從數學上來說，就是在平面內給定三個點A，B，C，找到平面內的第四個點P，使得P到A，B，C三點的距離之和最短.利用極值的有關結論，很容易得出問題的解.

由于表面張力的作用，液體的薄膜只有在它的面積為極小時才處于穩定平衡狀態.這是具有數學意義的種種實驗的取之不盡的源泉.如果膜的一部分邊界可以在給定的曲面（或平面）上自由移動，那么在這些邊界上，這個膜應垂直于給定的曲面.

利用這個事實，可以對上述問題及其推廣做明顯的演示.取兩塊平行玻璃板或透明塑料板，用三根或更多根短棒垂直地連接起來.如果我們把這個框架浸入肥皂水中，然后再提出來，那么，就可以得到一組垂直于兩平行板且連接著固定棒的薄膜.它在玻璃板上出現的投影，就是上述問題的解.

如果平板不是平行的，棒也不垂直于它們，或者板是曲面的，那么在這些板上薄膜形成的是曲線，這將說明新的邊分問題.

一個極小曲面中，三片曲面以120度的角相交于一線的現象，可以看作是有關施泰納問題現象在更高維空間的推廣.例如，如果我們用三條曲線連接空間中的兩點A，B，而且研究對應的肥皂膜穩定系統.最簡單的情形是取一條曲線為直線段AB，而其他兩條曲線是同樣的圓弧，其結果顯示在圖2中.如果兩個弧所在平面的夾角小于120度，則所得的薄膜是三片曲面，兩兩夾角均為120度；如果我們轉動兩條弧線，增大內角，那么這個薄膜將連續地變化成兩個平面圓弧片.

現在我們用三條較復雜的曲線來連接A和B.例如，可以取三條折線，其中每一條都由同一立方體中連接對角線上相對的兩個頂點的三條棱組成：我們得到三片全等的曲面，它們在立方體的對角線上相交（從圖1所示的薄膜中，刺破與選定的三條邊界相鄰的薄膜時，即可得到這個曲面系統）.如果我們讓連接A和B的三條折線移動，就可以見到這條三重交線變成曲線，而120度的夾角仍保持不變（如圖3所示）.

在n片極小曲面相交的定直線上的所有現象基本上都有這一類似的性質.它們是平面上n個點間的最短連線問題的推廣.

四、肥皂泡實驗的一些結論[3]

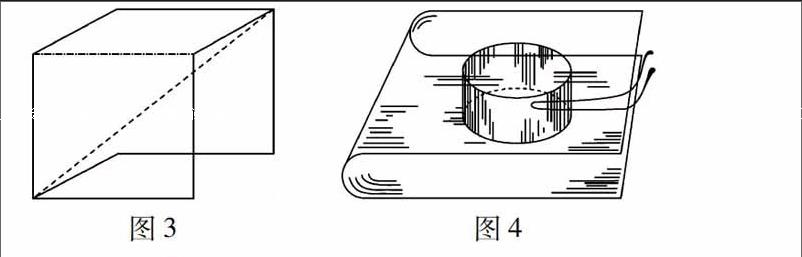
球形的肥皂泡表明，在包含一定體積的所有閉曲面中，球有最小體積.如果我們考慮體積一定，表面有收縮于極小傾向的肥皂泡，但對它加上某些限制條件，那么所得的曲面將不是球面，而是等平均曲率的曲面.例如，在事先用弄濕的兩塊平行玻璃板之間吹入一個肥皂泡.當這個肥皂泡碰到一個玻璃板時，馬上變為半平面形.而當它碰到另一塊板時，就躍變為圓柱形（如圖4所示）.

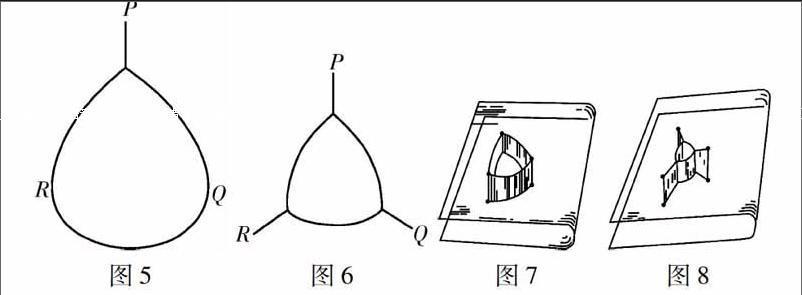
利用一根尖細的小管子，來增加或減少泡內空氣的總量，就可研究等圓問題解的性質.但是，利用吸出空氣，不能獲得彼此相切的圓弧.隨著空氣的減少，圓弧三角形的角，理論上不會小于120度，此時得到的形狀如圖5、圖6所示，當面積趨近于0時，它也會變為相交于一點且夾角都是120度的三條直線段.關于不能形成互切的圓弧，數學上的理由是：當肥皂泡和頂點分離時，連線不能計算兩次.對應的實驗可由圖7、圖8解釋.

在立體框架內吹進一個肥皂泡，如果泡膨脹到框架外，將得到一組以二次曲線為底的等平均曲率曲面.如果把泡內的空氣吸走，就能得到一系列美麗的結構.不同平衡狀態間的轉換和穩定現象是使這些實驗從數學上看很有啟發性的原因.這些實驗說明了穩定值理論，因為平衡狀態的轉換的發生導致曲面經過一個不穩定的平衡狀態.例如，圖1所示的立方結構，中心是一個鉛直平面，連接著各棱上的12片平面，這是不對稱的.因此，至少還有兩個其他的平衡位置，一個中心是鉛直的正方形，另一個中心是水平的正方形.事實上，用一個細管對著這個正方形的邊吹氣，可以迫使結構達到這樣的位置：正方形退化為一點，這一點就是立方體的中心；這個不穩定的平衡位置，立刻會轉變成另一個穩定位置，這個位置由原來的位置旋轉90度得到.

五、啟示

如果利用比前面所說的更黏的液體，更容易觀察到整個現象的變化.當然，這只是一種大致的考察，而不是數學證明.嚴格地說，物理事物的這個數學解釋是否適當，或者它是否僅給出物理現實的不充分的表象等問題依然存在.不可否認，一些實驗對我們研究某些問題會有不少的啟示.因此，如何有效開展數學實驗是值得我們深思的一個問題.

【參考文獻】

[1]老大中.變分發基礎[M].北京：國防工業出版社，2007.

[2]胡作玄.數學是什么[M].北京：北京大學出版社，2007.

[3]盛中平，王曉輝.什么是數學實驗[J].高等理科教育，2001（02）：25-28.

[4]李連昌.數學實驗放大了的數學課堂[J].數學教學通訊，2014（16）：2-3.

[5]吳曉.大學數學中的數學實驗教學[J].大學教育，2014（05）：116-117.

[6]孫小中.對數學實驗的一點思考[J].基礎教育研究，2016（02）：31.

[7]王猛.肥皂膜在中學物理實驗中的應用[J].物理之友，2014（01）：31-32.

[8]張恩賓.偏微分方程課堂實踐教學應用[J].現代經濟信息，2016（11）：455，457.