基于SIFT算法的全景圖像拼接技術研究①

文偉東, 張 明

(上海海事大學 信息工程學院, 上海 201306)

基于SIFT算法的全景圖像拼接技術研究①

文偉東, 張 明

(上海海事大學 信息工程學院, 上海 201306)

全景圖像拼接技術即通過將部分重疊區域的圖像合成以描述某個場景信息的360度圓形圖像. 引用一種新型的基于SIFT(尺度不變特征變換)特征匹配的圖像排序算法, 實現圖像的有序排列, 針對圖像拼接存在的誤匹配點較多、耗時較長等問題, 結合FAST算法進行特征點提取, 接著針對相鄰有序圖像間的亮度差異采用自動校正操作,削弱了相鄰圖像間的亮度差異, 并結合改進的Ransac算法剔除誤匹配點對, 最后用加權平衡算法實現圖像的快速融合. 實驗結果表明該優化排序算法穩定、高效.

全景圖像拼接; 圖像排序; 自動校正; 加權平衡; 融合

圖像拼接技術作為一大研究熱點, 主要用于計算機視覺和數字圖像處理領域. 圖像拼接技術即是將同一場景下的兩個或多個重疊圖像通過一系列數字圖像技術處理[1], 并且可以獲得包含所有原始圖像信息的新的全景圖像. 近年來, 該技術被廣泛應用于航天, 醫學,虛擬現實和日常生活等許多領域. 圖像配準即是找到兩個或更多個圖像的重疊部分, 并建立圖像之間的關系.圖像配準算法可以大致分為兩種類型[2], 一種是基于圖像特征的圖像配準, 另一種是基于區域的圖像配準.

基于特征的圖像配準通過使用圖像中匹配的局部不變特征來確定圖像之間的幾何變換關系. 1977年Moravec提出了角點特征和稱為“興趣點”的概念. 他通過灰度自相關函數來思考該像素和其領域像素的相似性. 1988年, Harris改進了Moravec角, 并提出了Harris角點檢測算法. 繼lindeberg提出了尺度空間理論之后, Mikolajczyk和Schmid提出了具有尺度不變特征的Harris-Laplacian檢測算子和Harris-Affine檢測算子. 2000年, Lowe[3]提出了高效SIFT(尺度不變特征變換)局部特征, 成為局部特征研究領域的里程碑.

文中引用一種基于SIFT特征提取的新型圖像排序算法. 在該方法中, 匹配特征首先通過計算一個圖像和其它圖像之間的匹配點的數量來獲得最近的圖像, 并逐一計算, 以最終獲得精確的圖像順序, 同時結合了高效的FAST算法獲取高斯金字塔圖像中的特征點對, 從而提升算法的運行效率; 接著針對有序相鄰圖像間的亮度差異, 實行相鄰圖像的亮度差異校正操作, 同時結合改進地Ransac[4]算法剔除錯誤匹配點對, 最后用加權平衡算法實現圖像的快速融合. 最終實現高質量、穩定的全景圖像.

1 特征點提取

1.1 SIFT特征點提取

1999年, David G. Lowe教授總結了現有的基于不變技術的特征檢測方法, 并在此基礎上提出尺度不變特征變換SIFT-圖像局部特征描述算子. SIFT基于尺度空間, 并且保持對圖像變換的不變性, 例如縮放, 旋轉和仿射變換. 并于2004年得到進一步改進.

SIFT特征提取和匹配的過程主要包括四個部分:SIFT特征檢測, SIFT特征描述, SIFT特征匹配和匹配點提純. 具體步驟如圖1所示.

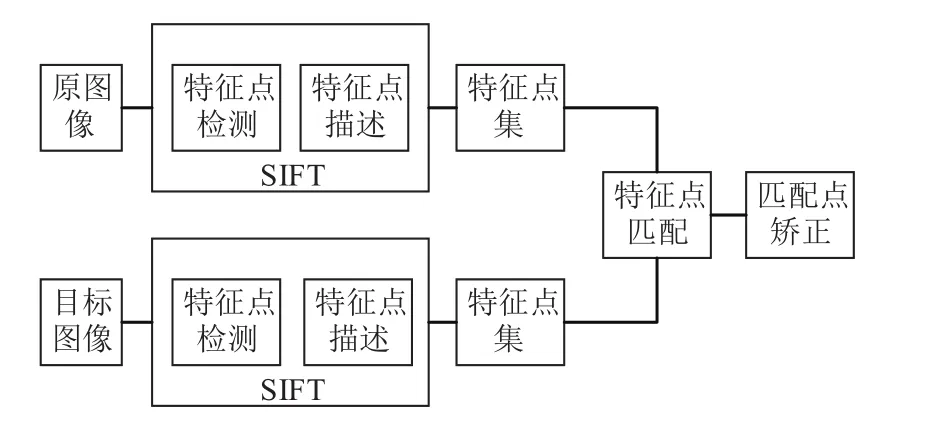
圖1 SIFT特征檢測和匹配的流程圖

SIFT特征提取的過程按如下順序: 極值檢測, 精確定位特征點位置, 計算特征點的主方向以及特征描述符生成.

SIFT算法通過在不同尺度空間上尋找關鍵點, 高斯模糊是獲取尺度空間的理論支撐[5], 即依據高斯模板和原圖像做卷積運算, 實現模糊圖像. N維空間的正態分布表示為:

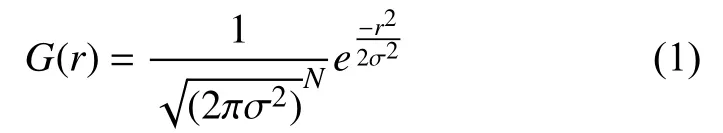
假設二維高斯模板大小視為m×n, 那么可得出模板上的元素(x, y)映射的高斯值計算公式為:

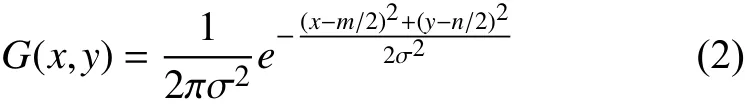
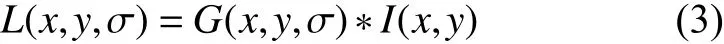
1.2 基于SIFT特征匹配的圖像排序算法

針對自動排序存在的問題, 如待拼接的圖像需要按順序輸入等, 研究人員提出了各種圖像排序算法. 本文基于SIFT特征匹配引入一種新型圖像排序算法[6]. 該算法可以實現圖像排序, 并且不需要任何手動干預.

I1, I2分別代表兩張圖像. 首先依次提取I1和I2的SIFT特征, 然后進行特征匹配. 在理想條件下, 只要I1和I2有重疊區域, 便可以獲取SIFT特征匹配點對. 如果沒有, 則無法獲取SIFT特征匹配點對. 根據這個分析, 本文引入一種基于SIFT特征匹配的圖像排序的算法, 設有圖像集, 集合R=NULL; 圖像的SIFT特征點集, P是存儲圖像匹配點對集合的向量, P=NULL. 具體算法步驟如下:

1) 從集合S中隨機選一張圖片Im, 1≤m≤n

2) A=1

3) 如果IA屬于R, 則令Im和IA的匹配點對集PA=NULL. 否則, 對Im和IA進行配準, 即對tm和tA進行SIFT特征匹配, 得到匹配點對集合PA; P=P+PA

4) A=A+1 如果A＞n, 轉到步驟5, 否則轉到步驟3

5) 計算集合P中Pi的元素個數di, 1≤i≤n, 得到

6) 找出集合D中的最大值dk, 1≤k≤n, Im的最佳匹配圖像是Ik, 將Ik加入集合R中, 即R=R+Ik

7) 使m=k, 更新n的值, n=n-1

8) 如果n=1, 跳到步驟9, 否則跳到步驟2

9) R=R+(S-R), 算法終止

由以上算法輸出的R即是圖像集序列, 該集合中的圖像在空間場景中有序排列, 能夠直接用于全景圖像拼接.

2 特征點匹配

SIFT算法雖具備旋轉不變、光照不變、尺度不變等很多優勢, 但該算法也存在如計算復雜度高、誤匹配點較多等缺點, 影響了全景圖像拼接的真實性, 本文在以下幾點進行改進. 結合FAST算法依據高斯差分金字塔圖像來實施特征點提取, 增強算法的運行效率, 針對相鄰圖像間的亮度差異, 采用圖像亮度差異自動校正操作, 便于特征點匹配; 同時采用改進的RANSAC算法剔除誤匹配點對, 實現更好的圖像融合.

2.1 結合FAST算法提取特征點

特征點檢測是圖像拼接技術的第一步, 對整個算法執行效率起著關鍵的作用. 傳統SIFT算法首先建立好高斯金字塔, 接著采取極值點檢測、關鍵點定位等方法, 復雜度較強. 而FAST算法作為公認的快速特征點檢測法, 通過計算某像素點和周圍像素點的灰度差,從而出該像素點是不是極值點, 大大降低了復雜性, 提高了算法的執行效率.

文中在SIFT圖像匹配技術中結合FAST算法, 最初隨機選取某個像素點P, 接著構造半徑為3的圓, 比較圓周上選取的16個像素點, 如果像素值中存在四分之三滿足公式4, 即P被視為角點. 圓周上任一點的灰度值視為Ix, P點的灰度值即為Ip, 已知的閾值常數t. 式中: 滿足界定前提的像素數量N, 當N超過給定閾值, 即P視為一個特征點.

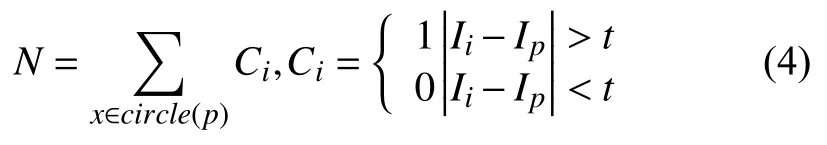
對現有高斯差分金字塔圖像結合FAST算法特征提取的主要過程如下:

1) 計算中心的點P像素值與圓周邊緣1到9編號的像素點存在的灰度差值, 判斷兩個值的絕對值大小是否超過給定閾值t, 如果都大于即P視為候選特征點, 繼續下一步計算.

2) 進一步計算點P的像素值和圓周邊緣上標有點5和點13像素點存在的灰度差值, 如果點1、9、5、13滿足四分之三即至少三個點差值大于給定閾值t或小于它的相反數-t, 即該點視為候選特征點, 繼續下一步計算.

3) 反復執行步驟1、2, 遵循準則檢測完圓周邊緣上16個像素點.

圖2為FAST特征點檢測的模板圖.

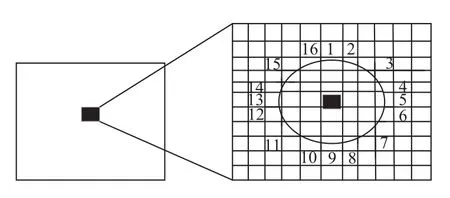
圖2 FAST特征點檢測模板圖

2.2 圖像亮度差異自動校正

由于主觀因素, 采集的原始圖像會出現不同程度亮度差異, 故在特征點檢測原始圖像之前先進行圖像亮度差異調整[7], 使得左右兩幅圖像亮度漸進一致, 從而獲得更有效的特征點, 同時能改善拼接痕跡, 實現更好融合效果.

根據前面圖像排序算法確定出的相鄰圖像的重疊區域, 通過重疊區域的像素均值削弱拍攝時帶來的亮度差異, 過程如下:

分別計算兩幅相鄰圖像重疊處的像素均值, 記為I1和I2, 即得到公共均值:

依據公共均值來調節I1和I2的亮度差異, 如下式所示:

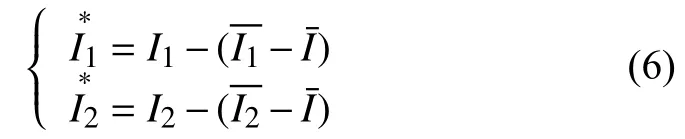
經調節后, 待拼接圖像的亮度整體保持一致, 接著按照特征點檢測與匹配操作, 實現高效提取角點、降低誤匹配率、圖像效果更清晰.

2.3 改進的Ransac算法剔除誤匹配點對

特征點提取后, 即需確定相鄰兩幅圖像之間特征點對應關系—特征點匹配. 本文通過歸一化相關法(NCC)[8], 其相關系數理論如下:

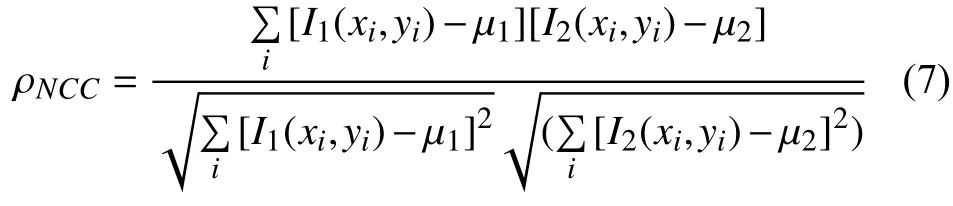
式中: μ1, μ2代表相關窗口的像素灰度平均值. 根據最大相關性雙向搜索圖像1、2, 當特征點彼此重合時, 即認為是一對匹配點, 通過該方法搜索直到所有的匹配點對被找到. 不難發現該算法獲取的匹配點對存在部分“偽點對”, 需通過Ransac(隨機一致性算法)對以上獲取的匹配點對進行過濾, 提高匹配精確率.

傳統的Ransac算法在外點較多時會構造錯誤模型,本文的Ransac算法在執行之前首先判斷特征點的方向是否相同, 提升匹配點對的準確率; 同時運用臨時模型預檢測方法以提高算法的執行效率. Ransac算法的基本思想: 對象樣本通常包含正常數據以及因種種原因生成的異常數據, 正確的模型通常由正常數據建立, 異常數據較此模型往往偏離較遠, Ransac算法使用迭代方式估計數學模型參數以獲取有效樣本數, 本文實現算法步驟如下:

1) 計算所有匹配對中特征點方向差, 接著建立位于0到360間含有36個區的直方圖, 即每個區為10°, 統計每區存在的匹配點對數量, 選取最大區匹配點對為候選匹配點對.

2) 依據以上得到的匹配點對中選取5對匹配點, 再從中隨機選取4對線性估計變換矩陣H, 找到臨時模型,繼而檢驗另外一對是否在模型上, 如不在即放棄重選, 否則作為候選模型并繼續尋找其支撐點集. 如公式(8)所示:

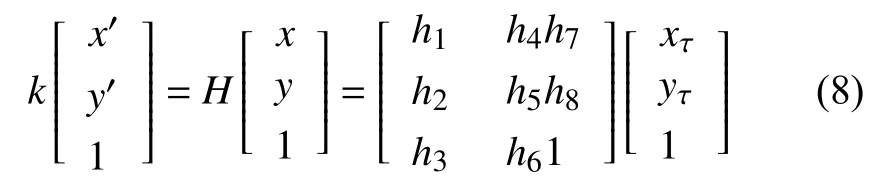
3) 計算所有匹配點對離H的垂直距離d, 依據d<閾值t判斷所有匹配點對的內點對, 多次實驗對比得出閾值取值越小越穩定, 當所有匹配點對中正確匹配點對數的比例不少于93%時, 即認為最佳匹配集合.

4) 重復以上步驟, 直到內點對集合最大, 記下H, 即為所求矩陣.

3 圖像融合

通常圖像有序拼接之后會存在明顯縫隙, 因此還需做融合處理[9]. 本文采用加權平衡算法, 其主要理論:引入漸進因子, 范圍在(0, 1)之間. 生成加權平均[10], 式(9): f11、f22、fw分別為基準圖像、待匹配圖像及融合后圖像.

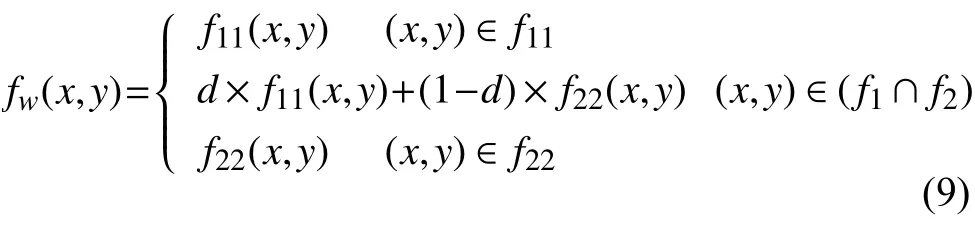
圖3 權值計算方法

4.2 全景圖像拼接實現

圖4是6張無序圖像, 這些圖像從左至右、從上之下分別I1～I6.

圖4 無序的圖片

使用1.2節中基于SIFT特征匹配的圖像排列算法,6張圖像的計算結果如表1所示.

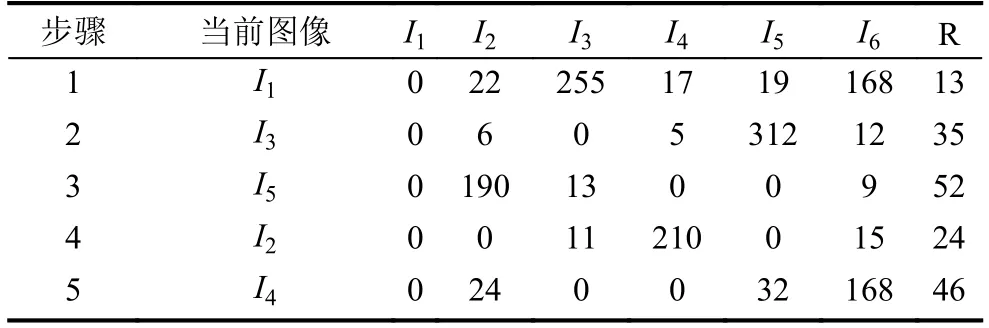
表1 基于SIFT特征圖像排序算法過程

在表1中, 交叉點處數字表示兩圖像之間匹配點數量. 根據R中最后一列和最后一行結果, 可得到排序后圖像, 實現了圖像有序排列.

為了驗證優化后算法的高效性, 隨機選取排序后相鄰兩張圖像進行實驗, 其中兩幅圖像之間特征點的連線即一組匹配對, 如圖5(a)和5(b)分別用于拼接的左右原始圖像, 圖6(a)和圖6(b)則代表原始的SIFT算法和改進優化后算法通過特征點配準所得實驗結果, 圖6(c)和7(d)則為最后得到的兩幅圖像的拼接效果.

以上實驗具體運行結果如表2所示, 每次實驗數據為重復五次實驗得到的數據均值.

4 實驗結果及分析

4.1 實驗說明

為了驗證改進后算法的可行性, 實驗環境硬件如

圖5 拼接實驗原始圖

圖6 原始算法和優化算法匹配效果

表2 正常實驗下的拼接數據

從表2中的實驗數據可以得出結論: 表2中算法改進前后完成匹配的時間分別是2.75 s和1.35 s, 效率進一步提升. 原因在于改進后的算法避免了原SIFT算法對每層高斯差分金字塔采取特征點提取造成的運算時間較長問題, 取而代之的是FAST檢測算法相結合, 快速完成特征點檢測, 進一步提高算法效率.

同時改進后的算法減少了誤匹配率, 由之前SIFT算法正確匹配率的89%提升到93.9%, 獲取到的匹配點對分別為52對和32對, 即改進后算法獲取到的匹配點對數較少, 從圖6(a)可以很明顯的看到誤匹配點對, 而圖6(b)將誤匹配點對進一步剔除; 原因在于Ransac算法在建立正確判斷模型之前采取了特征點對方向特征的判斷操作, 同時運用臨時模型預檢測思想, 從而剔除誤匹配點對, 同時從圖6(c)和圖6(d)對比可看出改進后算法因減少了誤匹配點對, 從而避免對應圖像關系錯位,即拼接圖像無明顯條紋、褶皺, 拼接效果更真實.

依據改進后的算法進行特征點匹配后, 進一步根據加權平衡算法實現圖像的快速融合, 最終實現圖像的全景拼接, 效果圖如圖7.

圖7 最終拼接全景圖

5 結論

針對全景圖像拼接在實際應用中存在的復雜性和誤匹配點對較多問題, 本文引入一種新型的基于SIFT特征提取的全景圖像自動排序算法, 實現了圖像全景拼接, 充分體現了該算法的自動性和適用性. 結合高效的FAST算法獲取高斯金字塔圖像中特征點對, 從而提升算法運行效率; 在特征點提取之前先調節圖像的亮度差異, 保證圖像視覺的一致性, 體現了圖像的真實性,同時通過改進的RANSAC算法剔除了大量誤匹配點對,提升了算法的精確度. 最終根據加權平衡算法實現圖像的快速融合. 實驗表明, 本文的算法優化在清晰度、準確度、效率和自動化程度方面均有較大提高.

1侯舒維, 郭寶龍. 一種圖像自動拼接的快速算法. 計算機工程, 2005, 31(15): 70–72.

2楊占龍, 郭寶龍. 基于興趣點偽澤尼克矩的圖像拼接. 中國激光, 2007, 34(11): 1548–1552.

3張朝偉, 周焰, 吳思勵, 等. 基于SIFT特征匹配的監控圖像自動拼接. 計算機應用, 2008, 28(1): 191–194.

4常青, 張斌, 邵金玲. 基于SIFT和RANSAC的特征圖像匹配方法. 華東理工大學學報(自然科學版), 2012, 38(6): 747–751.

5閆志, 王黎明, 陳平. 基于多目標優化的SIFT特征匹配算法. 現代電子技術, 2010, 33(12): 99–102.

6李曉娟. 圖像拼接技術研究[碩士學位論文]. 西安: 西安電子科技大學, 2007.

7王蕾. 圖像配準技術及應用研究[碩士學位論文]. 西安: 西安電子科技大學, 2007.

8Xu PF, Zhang L, Yang KY, et al. Nested-SIFT for efficient image matching and retrieval. IEEE MultiMedia, 2013,20(3): 34–36. [doi: 10.1109/MMUL.2013.18]

9Zhao WJ, Gong SR, Liu Q, et al. An Auto-sorting arithmetic for image sequence used in image mosaics. Journal of Image and Graphics, 2007, 12(10): 1861–1864.

10Lowe DG. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 2004,60(2): 91–110. [doi: 10.1023/B:VISI.0000029664.99615.94]

Research on Panoramic Image Mosaic Technology Based on SIFT Algorithm

WEN Wei-Dong, ZHANG Ming
(Information Engineering College, Shanghai Maritime University, Shanghai 201306, China)

Panoramic image mosaic technology is a 360-degree circular image that combines the images of some overlapping areas to describe a particular scene. In this paper, a novel image sorting algorithm based on SIFT (Scale Invariant Feature Transform) feature matching is proposed to achieve the orderly arrangement of images. Aiming at the problem that the image mosaic has many mismatch points and takes a long time,the FAST algorithm is used to extract feature points. And then, an auto-correcting operation is adopted for the brightness difference between the adjacent ordered images to reduce the brightness difference, and the modified Ransac algorithm is used to eliminate the mismatching points. Finally, the Weighted Equalization Algorithm is used to realize the Fast fusion of the image. The experimental results show that the algorithm is stable and efficient.

panoramic image stitching; image sorting; automatic calibration; weighted balance; fusion

文偉東,張明.基于SIFT算法的全景圖像拼接技術研究.計算機系統應用,2017,26(7):227–231. http://www.c-s-a.org.cn/1003-3254/5899.html

2016-11-20; 收到修改稿時間: 2017-01-16