加權無標度網絡病毒傳播和局部免疫策略研究①
劉瑞軍
(武夷學院 實驗室管理中心, 武夷山 354300)
加權無標度網絡病毒傳播和局部免疫策略研究①
劉瑞軍
(武夷學院 實驗室管理中心, 武夷山 354300)
為了進一步描述現實生活中復雜網絡的病毒傳播問題, 改進加權無標度網絡模型的傳統構造方法, 考慮流量帶寬和個體抵抗力兩個重要因子, 利用平均場理論模擬仿真病毒傳播過程, 對實驗數據進行分析, 驗證該模型的有效性. 現實生活中往往只能了解復雜網絡的局部拓撲信息,傳統病毒免疫策略大多基于全局拓撲信息, 在僅了解局部信息的前提下, 提出加權無標度網絡中基于局部最優的病毒免疫策略, 通過動態模擬病毒傳播的免疫仿真實驗, 與隨機免疫策略和目標免疫策略對病毒傳播影響進行比較, 驗證局部最優免疫策略的有效性.
加權無標度網絡; 病毒傳播; 流量帶寬; 個體抵抗力; 局部最優
1 引言
近年來, 隨著互聯網的日益普及, 改善了人們的生活環境, 同時也為計算機病毒的生存和發展提供了有利條件. 在社會高速發展過程中, 人類曾多次遭遇毀滅性的計算機病毒攻擊, 造成嚴重的經濟損失. 同時, 計算機病毒安全問題甚至關系到一個國家的安定穩定,一種微不足道的新型病毒很可能使整個國家甚至大半個世界的網絡陷入癱瘓, 不但給生活帶來不便, 甚至給國防帶來危機. 為了讓人類生活在安全的互聯網環境中, 從計算機病毒第一次出現后, 許多科學家就開始模擬病毒傳播, 希望能預測計算機病毒的傳播過程并有效的遏制病毒的泛濫.
1999年Faloutsos等人[1]發現, 互聯網表現出很強的冪律分布特點, 節點的度有很大的波動性[1,2]. 目前為止主要從兩種不同的角度來描繪互聯網的結構[1,3]. 盡管隨著時間的推移, 系統中的節點和邊在不斷增加, 但網絡拓撲結構特性卻不會發生很大的變化[4]. 大量研究表明網絡上的病毒傳播與網絡的拓撲結構有著密切的聯系[5-8], 在BA無標度網絡中, 當節點數近似無窮時, 病毒的有效傳播率閾值近似于0. 1998年, Steve White提出了五個關于計算機病毒研究問題[9], 其中最具爭議性的問題是理論上的計算機病毒傳播速率遠超于現實. 現實中感染30萬臺主機需24小時左右[10], 然后理論上計算機病毒感染100萬臺主機所需時間還不到1秒[11].
針對互聯網上病毒傳播速度現實與理論的巨大差異以及現實互聯網絡的增長模式, 本文建立了引入邊權值表示流量帶寬節點值表示個體抵抗力的改進加權無標度網絡模型. 根據模型, 分別觀察了初始感染節點的選擇、個體抵抗力差異、流量帶寬限制等對病毒傳播的影響. 以往的病毒免疫策略[12]研究, 大多基于對網絡全局拓撲信息而做出的, 現實生活中, 大部分復雜網絡[13]僅僅局限于了解其局部拓撲信息. 針對現實情況,本文提出了加權無標度網絡中基于局部最優信息的病毒免疫策略, 通過與隨機免疫策略和目標免疫策略的比較, 觀察其是否有效.
2 模型及理論分析
2.1 加權無標度網絡模型
傳統加權無標度網絡模型中, 邊權值wi,j通常表示節點i, j間的熟悉程度,, 病毒的有效傳播率正 比于越大, 表示i, j節點之間越熟悉, 相似度越大, 當其中一個節點感染病毒時, 另一個節點感染病毒的概率也越大; 反之, 表示i, j節點之間越陌生, 相似度越小, 當其中一個節點感染病毒時, 另一個節點感染病毒的概率也越小.
模型的構造算法[5]如下:
Step1. 增長: 從一個具有m0個節點的網絡開始, m0個節點相互連接, 每次引入一個新的節點i, 并且分別連到m個已存在的節點上, 假設與節點j相連, 則i, j之間的邊權值為, 這里
Step2. 優先連接: 一個新的節點與一個已經存在的節點i相連接的概率與節點i的度, 節點j的度之間滿足公式(1)關系:

經過理論和實驗證明, 無標度網絡的度分布滿足冪律關系, 度分布函數[5], 其中k為節點的度,r通常取2~3[14]之間的值.
2.2 改進后的加權無標度網絡模型
問題1. 計算機病毒在互聯網上的傳播速率遠低于理論值, 現實考慮病毒傳播速率緩慢的原因為病毒高峰期時由于傳輸路徑本身容量的限制而發生擁塞現象和個體本身的不同防護措施使其不容易被病毒感染,某些節點如果度相對較大, 說明比較重要, 它就會相對與其他節點具有更強的病毒抵御能力, 而且通過它的傳輸路徑容量也相對較大. 為此引入了流量帶寬和個體抵抗力因子. 其中, 用節點本身的權值vi表示每個不同個體之間擁有的不同抵抗力, vi越大, 個體抵抗力越強, 被病毒感染的幾率越低; 用節點之間的邊權值wi,j表示節點i, j之間的流量帶寬,越大, 表示該條路徑的容量越大, 發生擁塞的可能性越低, 病毒在該條路徑上傳播得越順暢, 個體抵抗力在這條路徑上發揮的作用相對就比較微弱. 反之, 病毒在該路徑上的傳播速度將受到相應的抑制.
問題2. 傳統加權無標度網絡模型構造方法存在以下弊端: Step1中網絡每增加一個節點, 均產生m條邊,節點和邊的增長都很規律, 但現實互聯網節點與邊的增長并不是特別規律.
根據問題1和問題2, 本文對傳統加權無標度網絡模型的構造方法進行改進, 具體構造算法如下:
Step1. 增長: 從一個只有1個節點的網絡開始, 該節點擁有抵抗力值v1, 每次引入一個新的節點j, 并且按概率pi分別與所有存在的節點相連, 假設與節點i相連, 則i, j之間的邊權值為wi,j, 抵抗力vi的值更新為v’i, 如公式(2):
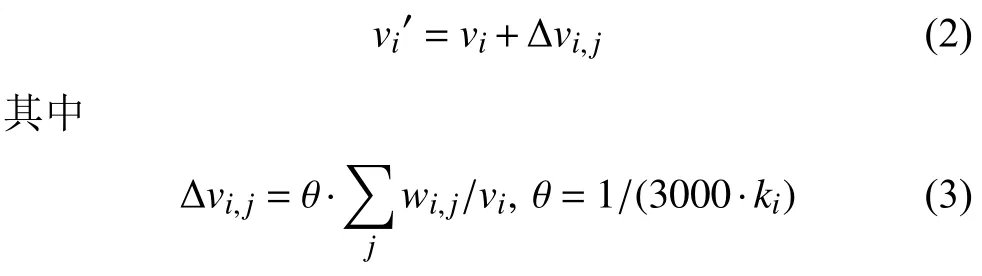
θ是增量因子, 根據節點i當前度的大小ki進行調節.表示節點i的當前總帶寬流量wi, 由公式(3)可知抵抗力增量與節點自身抵抗力呈負相關, 與節點帶寬總流量呈正相關, 重要的節點抵抗力增加的速度高于一般節點, 特別是相對重要的節點本身抵抗力較弱時, 人們就會對其重點保護, 大幅度提高其抵抗能力, 這與現實中的問題1相符.
Step2. 優先連接: 一個新的節點與一個已經存在的節點i相連接的概率pi與節點i的邊權和wi, 節點j的邊權和wj之間的關系如公式(4):
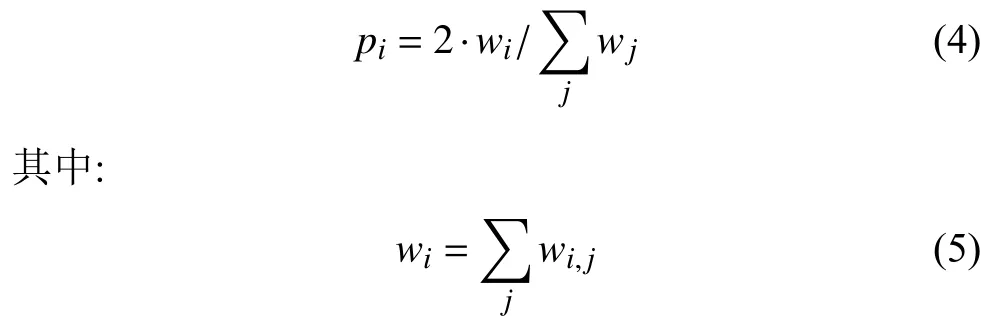
新增的節點偏向與網絡中的重要節點相連, 但也存在與微弱節點相連的可能.
Step3. 若新增加的節點經過Step1和Step2后仍是個孤立點, 則使其與網絡中相對序號最小的度最大節點相連.
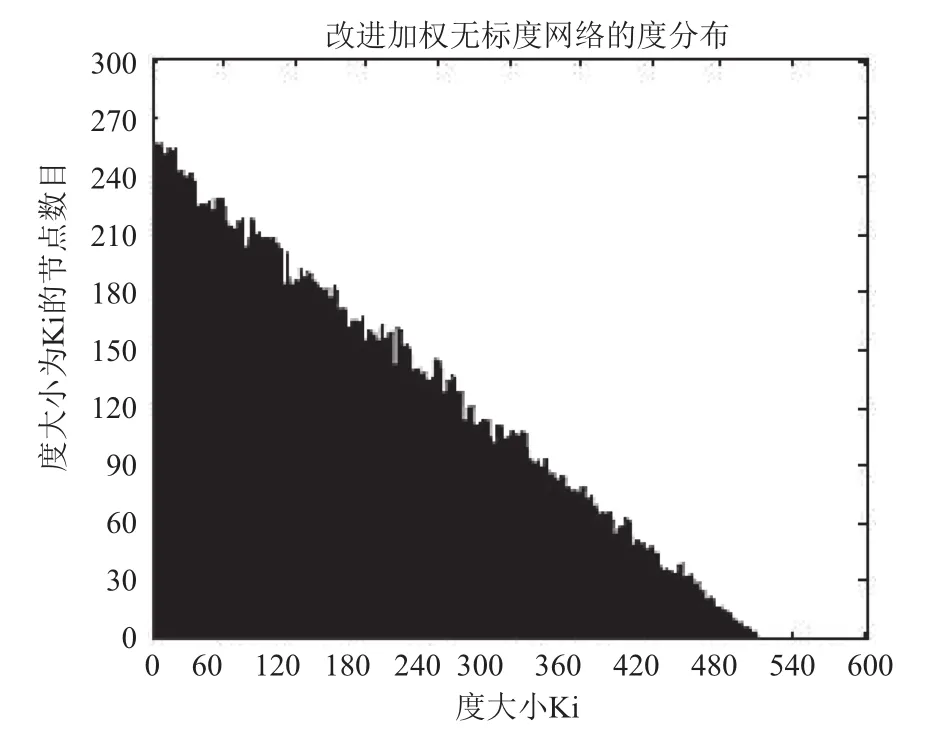
按上述算法構造出節點數目為5000個的改進后加權無標度網絡模型(具體參數設置請參見第五章節實驗結果與分析), 其度分布如圖2, 排除干擾點, 取其中的七組坐標數據進行計算, 坐標數據如表1, 計算結果的r值約為0.73, 即, 雖然與經典的r值在2~3之間有一定差距, 但由度分布圖可知改進的構造方式符合無標度網絡選擇增長和優先連接的特性, 具有現實網絡可參照性.
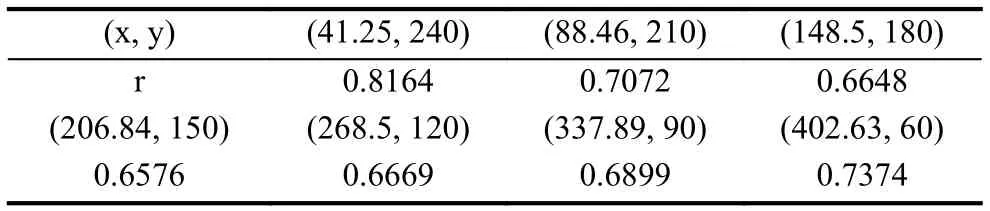
表1 度分布測試數據
3 動態模擬病毒傳播過程
通過研究無標度網絡上的SIS[15]和SIR[16]病毒傳播過程, 本文結合當前建立的改進后加權無標度網絡模型, 分析病毒在該模型上的SIS(R)傳播過程, 過程如圖1所示.
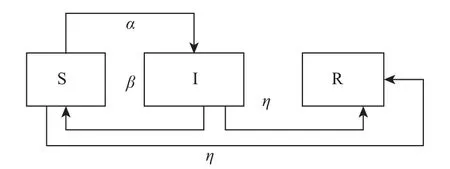
圖1 SIS(R)傳播模型
個體被劃分為三種不同的類型: 易感種群類(S), 他們不會感染其他個體, 但有可能被其他感染個體感染;感染種群類(I), 他們已經被感染, 而且會感染易感個體,具有傳染性; 免疫種群類(R), 他們是經過人為免疫策略而使其達到免疫狀態, 不會感染其他個體, 也不會被其他個體感染. 在圖2中, 若易感節點與感染節點接觸,它就有α概率的可能變成感狀節點; 感染節點本身有β概率的可能恢復到易感節點狀態. 無論是易感還是感染節點, 經過人為干預, 都有π概率的可能變成免疫節點. 研究中, 我們定義:
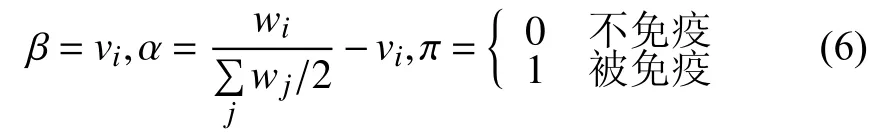
自我恢復率β與個體抵抗力vi相關, 如果被感染節點的個體抵抗力越強, 其恢復成易感節點的概率越高;被感染率α與該節點的邊權總和以及個體抵抗力相關,如果易感節點邊權和很大, 且其抵抗力相對較弱, 則其極易受感染; 免疫率非0即1, 如果對某點采取免疫措施,則其變為免疫狀態, 如果未采取任何免疫策略, 則其為原易感或感染狀態. 若不存在人為的免疫策略, 則SIS(R)模型退化為SIS模型.
利用平均場理論, 假設網絡中度值為k的節點中易感個體比例為, 感染個體比例為ρk(t), 免疫個體比例為, 其中Sk(t)+ρk(t)+Rk(t)=1, k=1, 2, ……, n. 建立公式(7)病毒傳播動力學方程如下:
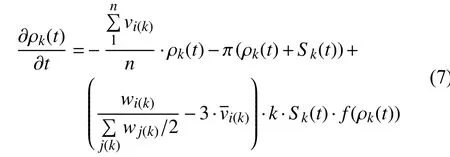
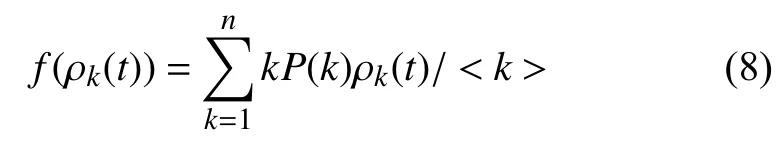
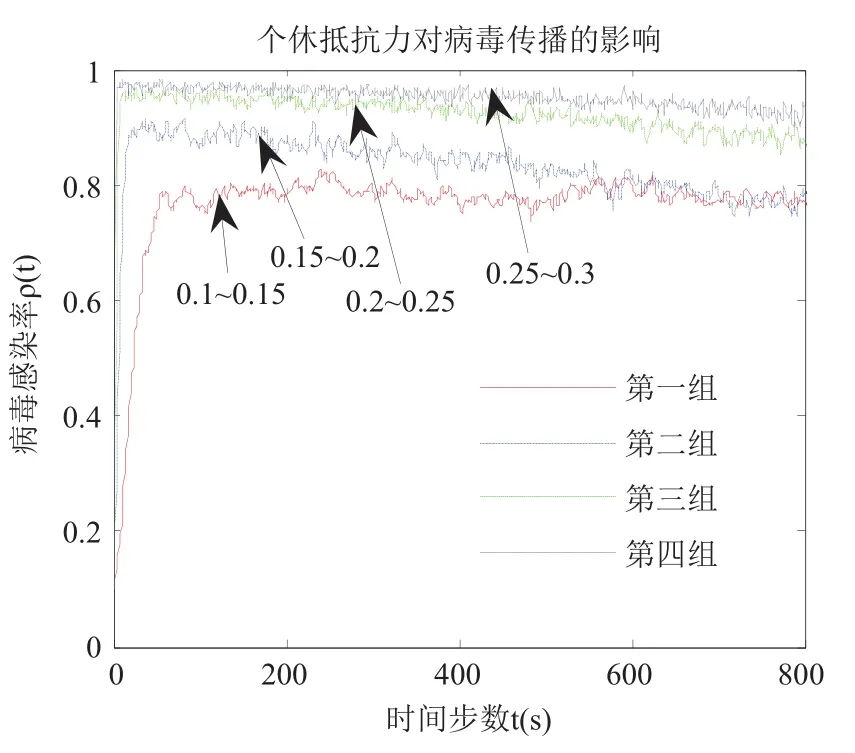
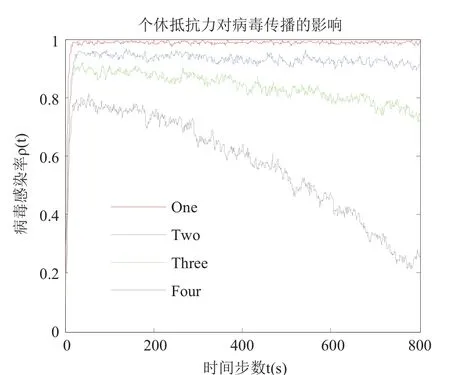
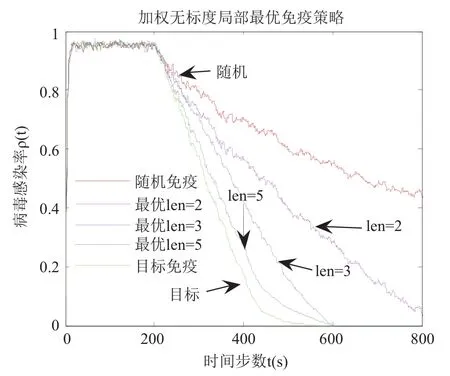
其中, n為節點的最大度值, P(k)表示度值為k的節點占所有節點的比例; 通過理論推導的公式(13)可知, 在無免疫策略前提下, 加權無標度網絡的病毒傳播的最終感染率與個體抵抗能力、度分布和邊權帶寬值之間密切相關. 4.1 傳統病毒控制策略 抑制病毒傳播的一種重要方法是人為干預, 引入免疫策略. 目前, 主要的免疫方法有隨機免疫策略、目標免疫策略和熟人免疫策略[17]. 本文僅討論隨機免疫和目標免疫策略. 隨機免疫策略通過隨機的方式選取若干個節點進行免疫, 不考慮節點中的個體差異, 每個節點被選到的概率都相等, 實驗表明, 隨機免疫雖然能局部抑制病毒的傳播, 但對于要徹底消滅病毒, 需對網絡中的絕大多數節點進行免疫, 這顯然不現實. 目標免疫策略優先選取網絡中重要的節點進行免疫, 考慮節點間的差異, 越重要但本身越脆弱的節點首先被考慮進行免疫, 實驗表明, 僅對少量節點進行免疫就可以達到徹底消滅病毒的目的. 4.2 基于局部最優病毒控制策略 傳統的隨機免疫和目標免疫均為基于網絡全局拓撲信息的免疫策略, 然后現實生活中對一個網絡全局信息的掌握十分有限, 特別是對一些龐大的復雜網絡.傳統的免疫實驗大多預先對需要免疫的節點進行免疫,然后再觀察病毒的傳播現象, 與現實生活中的實時免疫相悖. 因此, 針對上述問題, 本文提出了基于局部最優信息的動態免疫策略. 出于現實考慮, 假設(1): 每次動態地選擇N個點進行免疫, 而不是一次性把該免疫的節點全部免疫了. 假設(2): 由于發現病毒的滯后性, 當采取免疫措施時病毒已達到感染峰值. 假設(3): 由于不能全局性的發現病毒存在, 實驗中每個階段僅知道部分節點感染病毒, 即病毒獲知率S為0~1之間的數值.該免疫策略關鍵步驟如下: Step1. 對所獲知的被感染節點i, 計算與i相距len(直接相連距離為1)距離以內所有臨近節點各自的容量和wx, x表示網路中以i節點為中心, 以len為半徑的所有節點集, 表示與i節點臨近的節點集各自的容量和. Step2. 對wx中所有節點的容量和進行從大到小排序, 選擇前N個節點進行免疫. 若n(Wx) Step3. 若n(Wx)=0, 結束計算, 否則轉Step1. 仿真實驗過程, 改進后加權無標度網絡的節點規模為5000個, 通常情況下足以體現現實復雜網絡模型的主要病毒傳播特征. 個體抵抗力vi取0.01~0.05之間的數值, 節點間的流量帶寬取0.1~0.3之間的數值,基于局部最優免疫策略算法過程中感染病毒節點的獲知率S設置為0.1~0.5之間以及距離len值取1~5之間的整數, 初始感染率統一取值為0.1, 即隨機選取網絡中十分之一的節點為被感染節點, 其他均為易感節點.按改進后的加權無標度網絡構造算法構造出網絡模型的度分布如圖2所示, 具體數據分析見表1. 圖2 改進后加權無標度模型的度分布 5.1 流量帶寬大小對病毒傳播的影響 現實的病毒傳播速度與理論存在巨大差異, 為驗證所述流量帶寬是否為影響病毒傳播的因素之一, 本文對在僅流量帶寬變化的情況下對病毒傳播行為進行仿真實驗. 仿真中, vi取0.02~0.03之間數值,分別取表2中的四組測試數據. 表2 流量帶寬測試數據 四組數據的流量帶寬逐漸增加, 仿真結果如圖3所示. 由圖3可知, 無標度網絡中隨著整體流量帶寬大小的增大, 病毒傳播速度和最終病毒感染率都隨之增加.當流量帶寬均值在0.2以上時, 病毒傳播行為基本不受太大影響, 只是在小范圍內波動. 由此得知, 流量在一定閾值范圍內可以抑制病毒傳播行為, 同時也驗證了實際生活中病毒大量爆發時由于帶寬的限制而相互制約, 從而導致傳播速度小于理論值. 5.2 個體抵抗力強弱對病毒傳播的影響 每個個體對同一種病毒的抵抗力不盡相同, 當一個個體的抵抗力強度較大時, 不僅能較快地從感染狀態恢復到易感狀態, 而且能在一定程度上遏制病毒對自身的感染. 為了進一步了解加權無標度網絡上個體抵抗力強弱對病毒傳播的影響, 仿真中取0.1~0.2之間數值, vi分別取值0.01~0.02、0.02~0.03、0.03~0.04和0.04~0.05四組數據進行測試, 仿真結果如圖4所示. 圖3 流量帶寬大小差異 圖4 個體抵抗力強弱差異 從圖4可以看出, 加權無標度網絡中, 節點抵抗力強弱差異對病毒傳播速度的影響較小, 對病毒峰值的影響較大, 當初始個體抵抗力強度達到0.05左右時, 由于抵抗力隨時間不斷增大, 最終將影響最終的病毒感染比例. 個體抵抗力強弱將最終印象病毒的感染比例. 5.3 基于局部最優免疫策略對病毒傳播的影響 為了驗證加權無標度網絡上基于局部最優病毒傳播免疫策略的有效性, 對病毒傳播采取了免疫措施. 仿真中取0.1~0.2之間數值, vi取0.02~0.04之間數值,S =0.15且len分別取2, 3, 5, 觀察len在不同取值時對局部最優免疫效果的影響, 并與隨機免疫、目標免疫進行了比較, 效果如圖5所示. 圖5 加權無標度局部最優免疫效果 由圖5可以看出局部最優免疫策略相對于目標免疫策略和隨機免疫策略來說都是一種有效的免疫方法,雖然局部最優免疫策略的效果不如目標免疫策略, 但隨著len的增大, 局部最優免疫策略的效果將接近目標免疫, 當len取值為5時, 最優免疫策略的效果已經非常接近目標免疫了. 現實世界中, 很難了解網絡的全局信息, 所以局部最優免疫策略具有現實意義. 計算機病毒的日益泛濫嚴重威脅著網絡安全, 了解病毒在復雜網絡上的傳播行為及其性質對我們采取免疫措施至關重要. 不同的網絡采取的免疫措施不同,同一種網絡采取不同的免疫措施效果也不同. 經過仿真研究, 驗證了加權無標度中基于最優免疫策略對病毒傳播抑制的有效性, 特別是在僅僅了解局部信息的前提下, 大大提高了性價比. 在現實工作中, 我們可結合局部最優免疫策略對病毒采取免疫措施, 從而提高網絡系統的可靠和安全性. 本文的研究中, 僅考慮只有一種病毒存在的傳播模型及免疫策略, 然而現實生活中計算機往往同時存在多種病毒. 不同病毒之間在復雜網絡上的相互競爭與合作關系值得我們進一步深究. 1Faloutsos M, Faloutsos P, Faloutsos C. On power-law relationships of the Internet topology. ACM SIGCOMM Computer Communication Review, 1999, 29(4): 251–262.[doi: 10.1145/316194] 2Vazquez A, Pastor-Satorras R, Vespignani A. Large-scale topological and dynamical properties of Internet. http://arxiv.org/abs/cond-mat/0112400. 3Chen GR, Fan ZP, Li X. Modelling the complex Internet topology. Complex Dynamics in Communication Networks.Berlin, Springer-Verlag. 2005. 213–234. 4李濤, 關治洪, 吳正平. 病毒在無標度網絡上的傳播及控制仿真研究. 計算機應用研究, 2007, 24(12): 177–178. [doi:10.3969/j.issn.1001-3695.2007.12.056] 5汪小帆, 李翔, 陳關榮. 復雜網絡理論及其應用. 北京: 清華大學出版社, 2006. 6WANG CX, Knight JC, Elder MC. On computer viral infection and the effect of immunization. IEEE 16th Annual Conference Computer Security Applications. New Orleans,USA. 2000. 246–256. 7Vázquez A, Pastor-Satorras R, Vespignani A. Large-scale topological and dynamical properties of the Internet. Physical Review E, 2002, (65): 066130. [doi: 10.1103/PhysRevE.65.066130] 8Li X, Chen GR, Li CG. Stability and bifurcation of disease spreading in complex networks. International Journal of Systems Science, 2004, 35(9): 527–536. [doi: 10.1080/00207720412331285869] 9White SR. Open problems in computer virus research. Proc.of Virus Bulletin Conference. Munich, Germany. 1998. 10Moore D. The spread of the code-red worm. http://www.caida.org/research/security/code-red/coderedv2_analysis.xml. 11Staniford S, Moore D, Paxson V, et al. The top speed of flash worms. Proc. of the 2004 ACM workshop on Rapid malcode.Washington DC, USA. 2004. 33–42. 12朱剛, 張寧, 馬良. 復雜網絡上計算機病毒傳播和控制策略研究. 計算機應用研究, 2006, 23(9): 54–56. 13黃金源, 張寧, 肖仰華. 基于拷貝模型的復雜網絡魯棒性研究. 計算機應用研究, 2010, 27(4): 1403–1406. 14Dorogovtsev SN, Mendes JFF, Samukhin AN. Structure of growing networks with preferential linking. Physical Review Letters, 2000, 85(21): 4633–4636. [doi: 10.1103/PhysRevLett.85.4633] 15Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks. Physical Review Letters, 2001, 86(14):3200–3203. [doi: 10.1103/PhysRevLett.86.3200] 16Zhou T, Fu ZQ, Wang BH. Epidemic dynamics on complex networks. preprint physics/0508096, 2005. 17Cohen R, Havlin S. Scale-free networks are ultrasmall.Physical Review Letters, 2003, 90(5): 058701. [doi: 10.1103/PhysRevLett.90.058701] Research on the Local Immunization Strategy of Virus Spreading in Weighted Scale-Free Networks LIU Rui-Jun In order to further describe the virus propagation of real-life complex networks, this paper improves the traditional construction methods of weighted scale-free networks model which considers two key factors: flow bandwidth and individual resistance. Using mean-field theory to simulate the process of the virus transmission, this article analyses the experimental data and verifies the validity of the new model. Most real-life complex networks are known to us with only the local topology information and the traditional virus immunization strategies are based on global network topology information. In condition of knowing local topology information, this paper proposes the immunization strategy of virus spreading based on the local optimum in weighted scale-free networks. Compared with the random immunization strategy and target immunization strategy about the efficiency of virus spreading in weighted scale-free networks, the local optimum immunization strategy is verified to be valid through the dynamic simulation of virus propagation. weighted scale-free networks; virus spreading; flow bandwidth; individual resistance; local optimum 劉瑞軍.加權無標度網絡病毒傳播和局部免疫策略研究.計算機系統應用,2017,26(7):263–268. http://www.c-s-a.org.cn/1003-3254/5835.html 福建省教育廳基金(JK2012056) 2016-10-13; 收到修改稿時間: 2016-11-28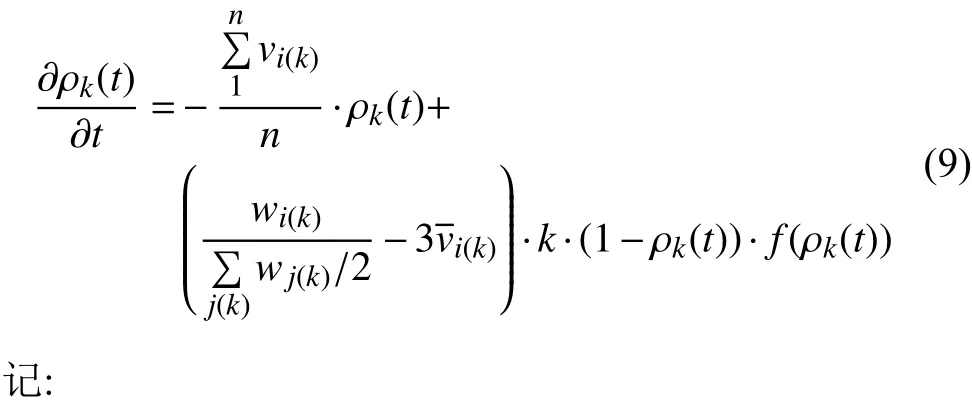
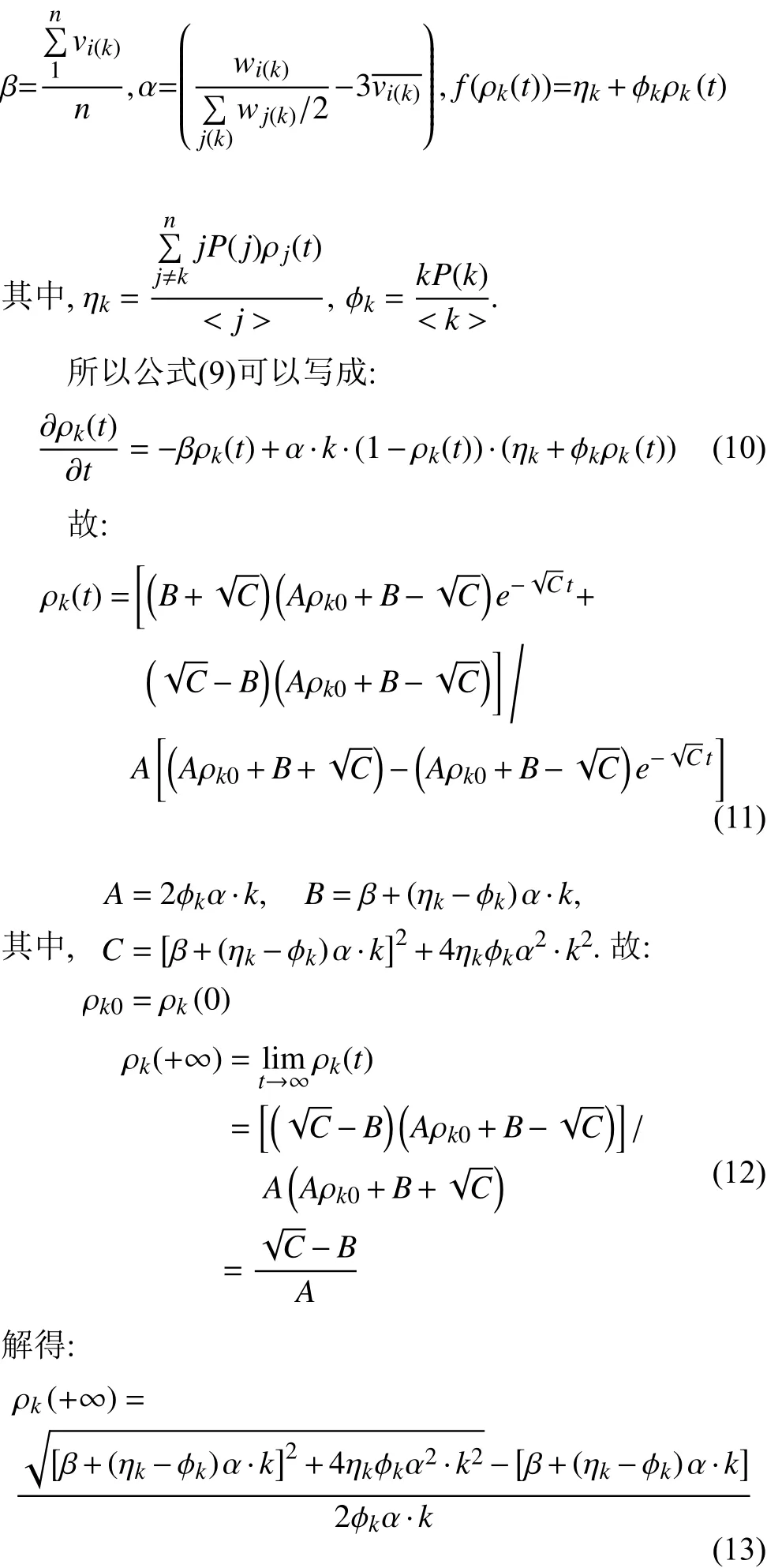
4 病毒控制策略
5 實驗結果與分析
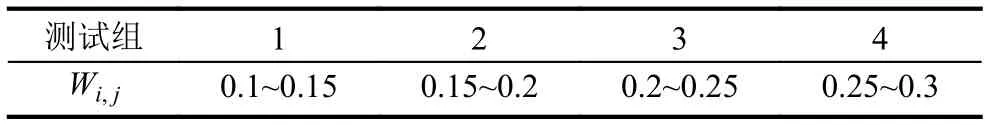
6 結束語
(Laboratory Management Center, Wuyi University, Wuyishan 354300, China)

