初中數學解題中數形結合思維的引入實踐微探

葉玉娣

（浙江省杭州市桐廬縣舊縣中心學校，浙江杭州 311500）

數學作為一門邏輯性要求較強的科目，對初中生而言是一項學習挑戰。數學課程作為數與形的結合，只有把握好數與形間的本質，才能準確解答出問題。數形結合思想作為初中生必須要具備一種解題思想，將其應用至解題活動中，有助于學生更好把握數學知識，依據知識間聯系構建知識體系，從整體上提升解題能力。

1 在數與式中的應用

為了使學生能夠理解數形結合思想的本質，教師需要在課堂教學中以問題解析的方式，為學生重點講解此方法的應用技巧。如，教師在教學有關正負數的知識時，事先畫出數軸，并邀請學生介紹數軸中對應數字的具體含義，旨在加深學生對于數軸中各項數值的認知。在學生掌握一定基礎后，為學生設計如下問題，鼓勵學生自主解答。

已知數 a、b、c在數軸上的位置如圖所示，化簡|a+b|-|c-b|的結果是 ______．

解析：先從數軸上a、b、c的位置關系可知：c＜a＜ 0；b＞ 0且 |b|＞ |a|，接著可得 a+b＞ 0，c-b＜ 0，然后即可化簡|a+b|-|c-b|可得結果。

解：由數軸上點的位置可得：c＜ a＜ 0＜ b，且|a|＜ |b|，∴ a+b＞ 0，c-b＜ 0，則 |a+b|-|c-b|=a+b+cb=a+c.故答案為：a+c

2 在變化規律中的應用

規律型問題的解題方法大多是借助觀察，對比特殊變量或位置，從中截取數據特征，將獲取的數據進行分組比較。但是此種解題方式過于繁瑣，為了節省時間可以采取數形結合的方法，雖然圖形和數字的形式不同，但它們可以表示相同的規律，從而幫助學生更好把握知識間的內在關聯，從而建立知識間的數形聯系，不斷提高解決效率。

如：有一個四等分轉盤，在它的上、右、下、左的位置分別掛著“眾”、“志”、“成”、“城”四個字牌，如圖1．若將位于上下位置的兩個字牌對調，同時將位于左右位置的兩個字牌對調，再將轉盤順時針旋轉90°，則完成一次變換．圖2，圖3分別表示第1次變換和第2次變換．按上述規則完成第9次變換后，“眾”字位于轉盤的位置是（ ）

A．上 B．下 C．左 D．右

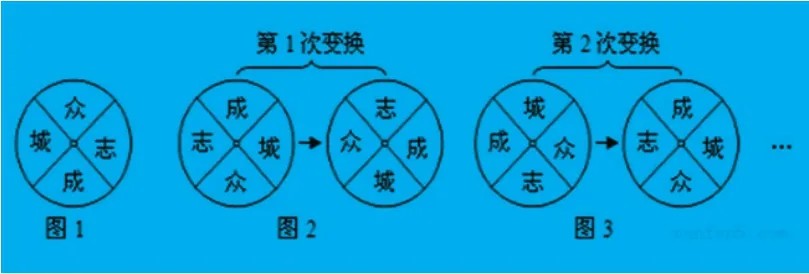
解析：根據題意可知每一次變換后相當于逆時針旋轉了 90°，經過 4次變換后會回到原始位置，所以按上述規則完成第 9次變換后，相當于第一次變化后的位置關系，分析比較可得答案．

解：根據題意可知每一次變換后相當于逆時針旋轉了 90°，經過 4次變換后會回到原始位置，所以按上述規則完成第 9次變換后，“眾”字位于轉盤的位置是應該是第一次變換后的位置即在左邊， 比較可得C符合要求。

3 在二次函數與不等式組中的應用

在解答此類問題時，依據數學題干中給出的條件，判斷問題最終求的是什么。以求解不等式或不等式組解集這類問題為例，需要事先確定題干中字母的取值范圍。雖然此種方式的理解難度比較大，但是若是能尋找到技巧，分析多個條件，將會獲取事半功倍的效果。

方程 7x2-（k+13）x+k2-k-2=0（k是實數）有兩個實根α、β，且0＜α＜1，1＜β＜2，那么k的取值范圍是（ ）

A．3＜k＜4

B. -2＜ k＜ -1

C．3＜ k＜ 4或 -2＜ k＜ -1

D．無解

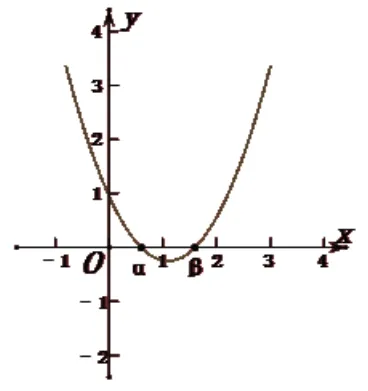
分析：若用數形結合的方法，先畫出拋物線 y=7x2-（k+13）x+k2-k-2的草圖，

易知當 x=0時，y＞ 0 ，k2-k-2＞0，所以k＞2或＜-1；當x=1時，y＜0，k2-2k-8＜0，所以-2＜k＜4

當x=2時，y＞0,k2-3k＞0，所以k＞3或k＜0

解不等式組可得k的取值范圍是3＜k＜4或-2＜k＜ -1， 故選 C．

4 在函數中的應用

函數作為初中數學教學的一大難點，也是最令學生感到棘手的知識。基于此情況，教師在解題教學中需要引導學生巧用數形結合思想，將數量關系借于圖形及其性質，使其直觀化，形象化，從而使問題得以解決。

二次函數 y=ax2+bx+c的圖象的頂點在第三象限 ,且不經過第四象限,則此拋物線開口向_______ ，c的取值范圍______ ，b的取值范圍______ ，b2-4ac的取值范圍______。

解：由題意畫出圖象，如圖：

從而判斷：a＞0, c≥0

∴對稱軸：x=-＜0

∴b＞0

圖象與x軸有兩個交點：

∴ ＞ 0 即 b2-4ac＞ 0

5 在函數圖形中的應用

由于學生對函數圖像特征缺少深入的了解，導致在解題過程中很難準確把握解析式，兩者轉換非常困難，解題效果無法達到預期效果。基于此問題，教師需要引導學生深度研究其本質，在解題過程中巧用數形結合思想，培養學生的數學思維，展開針對性的訓練，從而幫助學生更快理解并掌握其知識。

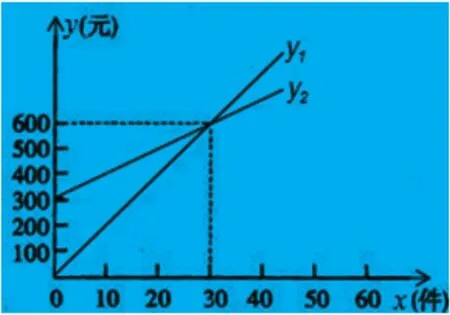
某公司推銷一種產品 ,設 x(件 )是推銷產品的數量 ,y(元 )是推銷費 ,如圖表示了公司每月付給推銷員推銷費的兩種方案 ,看圖解答下列問題 : 求y1與y2的函數解析式；解釋圖中表示的兩種方案是如何付推銷費的；如果你是推銷員,應如何選擇付費方案.

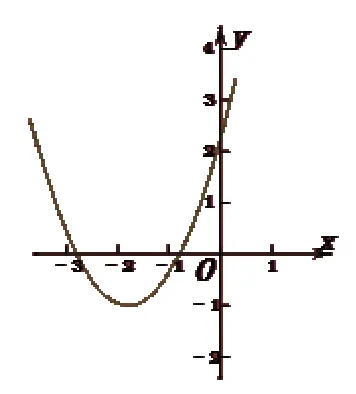
本題主要考察了用待定系數法求一次函數這一內容，在解答此題時可以采取數形結合思想，能夠使解題過程變得更加簡單。在解答第一問時，由圖已知兩點，可根據待定系數法列方程，求出函數關系式；在解答第二問時，根據兩條直線的截距和斜率，可解釋兩種方案的推銷費用；在解答第三問時，由圖可看出兩直線的交點為 30，當x＞30時，y1可獲得較多的推銷費用，當x=30時，兩種方案獲得的推銷費用一樣；當x＜30時，y2可獲得較多的推銷費用。

綜上所述，數形結合思想的引用為提升學生學習能力帶來諸多幫助，借助數與形間的轉換，全面解讀數學問題，培養學生數學思維，進一步提升了學習成績。因此，教師需要提高對數形結合思想的重視，開展多種類型的解題訓練活動，以此不斷提升學生的解題能力。

[1] 王愛花.初中數學數形結合思想教學研究與案例分析[J].中國校外教育,2017(05)

[2] 蔡清潤.數形結合教學方法在初中數學中的運用[J].西部素質教育,2017,3(01)

[3] 吳耀耀. 基于新課程標準下中學數學“數形結合”的教與學[D].寧夏師范學院,2016.