再論Devaney混沌的隨機性質
張新敏
(西南石油大學理學院, 四川成都610500)
再論Devaney混沌的隨機性質
張新敏
(西南石油大學理學院, 四川成都610500)
拓撲動力系統相關動力性質(如弱混合、拓撲弱混合、敏感性)之間的關系一直是動力系統研究的主要問題。證明利用相關函數定義的弱混合拓撲動力系統必為拓撲弱混合。以此為基礎,得到的系統是multi-敏感的和初值敏感依賴的。從而改進了相關文獻的主要結果。
弱混合;拓撲弱混合;multi-敏感
引言
貫穿全文,記N={1,2,3,…},Z+={0,1,2,…}。設(X,d)為非平凡的緊致度量空間,映射f:X→X連續,則稱(X,f)為一動力系統。對動力系統混沌行為的數學研究始于Li T Y和Yorke J A[1],即后來為大家所熟知的Li-Yorke混沌。簡而言之,混沌是指系統在沿著時間維度演變的過程中,其微觀個體的狀態相對于人們預測能力而言的不確定性;它是系統復雜性的重要量度。基于學者們對于復雜性的不同理解,各種各樣的混沌定義層出不窮,如Li-Yorke混沌、Devaney混沌、稠混沌、全局混沌、分布混沌、Li-Yorke敏感。其中,比較有影響力的是Devaney混沌。
混沌另外一個顯著的特征是對初值的敏感依賴性。稱動力系統(X,f)是初值敏感依賴的,如果存在ε>0,使得對任意x∈X及任意δ>0,存在y∈B(x,δ):={y∈X:d(x,y)<δ}及n∈Z+,滿足d(fn(x),fn(y))>ε。
定義1[2]稱動力系統(X,f)是Devaney混沌的, 如果以下條件得到滿足:
(1) (X,f)是拓撲傳遞的,即對任意非空開子集U,V?X,存在n∈Z+,使得fn(U)∩V≠φ;
(2)f的周期點在X中稠密;
(3) (X,f)是初值敏感依賴的。
值得注意的是,Banks等[3]證明了周期點稠密的拓撲傳遞系統是初值敏感依賴的。文獻[4]得到了幾乎周期點稠密的拓撲傳遞系統是初值敏感依賴的。后來,Moothathu[5]引入了更廣義的敏感性——syndetic-敏感、cofinite-敏感和multi-敏感。同時證明了非極小的syndetic-傳遞系統是syndetic-敏感的,并且對于syndetic-傳遞系統,初值敏感依賴蘊含syndetic-敏感。近來,吳新星等[6]得到了乘積系統是multi-敏感的當且僅當存在某個因子系統multi-敏感的。
集合A={a1
集合A?Z+是thick的,如果它包含任意長的整數段,即對任意n∈N,存在an∈A,使得{an,an+1,…,an+n}?A。全體thick集記為Ft。
對任意U?X及任意δ>0,定義
Nf(U,δ)={n∈Z+:diam(fn(U))>δ}
定義2[5]稱動力系統(X,f)是
(1) syndetic-敏感的,如果存在δ>0,使得Nf(U,δ)∈Fs。
(2) cofinite-敏感的,如果存在δ>0,使得Nf(U,δ)為有限余的。
(3) multi-敏感的,如果存在δ>0,使得對任意n∈及任意n個非空開子集U1,…,Un?X,恒有φ。
1預備知識
如果U,V?X,定義回復時間集為
N(U,V)={n∈Z+:fn(U)∩V≠φ}= {n∈Z+:f-n(V)∩U≠φ}
如果乘積系統(X×X,f×f)是拓撲傳遞的,則稱動力系統(X,f)是拓撲弱混合的。
下面命題給出了拓撲弱混合的若干等價刻畫:
引理1[7]設(X,f)為動力系統,則以下命題等價:
(1) (X,f)是弱混合的;
(2) 對任意非空開子集U,V?X,N(U,U)∩N(U,V)≠φ;
(3) 對任意非空開子集U,V?X,N(U,U)∩N(V,U)≠φ;
(4) 對任意非空開子集U,V?X,N(U,V)為thick集;

設μ為(X,d)上的Borel-概率測度,滿足supp(μ)=X,其中supp(μ)表示測度μ的支撐。 對于定義在X上的連續函數φ,φ,定義它們的相關函數為:
Cφ,φ(n)=∫X(φ°fn)φdμ-∫Xφdμ∫Xφdμ。
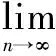
Xu Z J等[8]于2004年證明了強混合的動力系統必為拓撲傳遞和初值敏感依賴的。近來,王濤和賈諾[9]改進了該結果,得到弱混合的動力系統是拓撲傳遞的; 如果附加周期點稠密性,則該系統必為初值敏感依賴的。吳新星和朱培勇[10-11]系統研究了連續區間映射的敏感依賴性。馮漢等[12-13]研究了動力系統的一些混沌性質及其應用。近來,李瑞佳和朱培勇[14]得到了強傳遞集的一些基本性質。本文以文獻[8-9]為基礎,進一步證明了弱混合的的動力系統是拓撲弱混合和multi-敏感的。從而改進了文獻[8-9]的主要結論。同時,該結果更加深入地闡述了弱混合和拓撲弱混合之間的聯系。
2主要結果
定理1如果動力系統(X,f)是弱混合的,則(X,f)是拓撲弱混合的。
證明任取X的非空開子集U,V,同時令ε=μ(U)μ(V)。由測度μ的正則性(文獻[15]定理6.1)知,存在非空閉子集A?U,B?V,使得μ(A)μ(B)>7ε/8。同時注意到X為正規空間, 由Urysohn-引理得存在連續函數φ:X→ [0,1]和φ:X→[0,1],使得如下條件成立
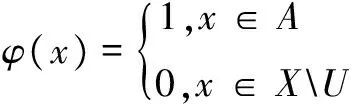
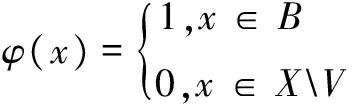
由于(X,f)是弱混合的,所以
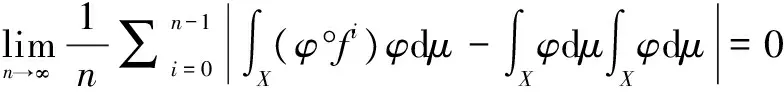
因此
由此結合φ,φ的選取知,
0<∫X(φ°fn)φdμ=∫f-n(V)∩U(φ°fn)φdμ≤μ(f-n(V)∩U)
這說明N(U,V)={n∈Z+:f-n(V)∩U≠φ}?P為thick-集(因為P的密度為1)。由引理1自然可得, (X,f)是拓撲弱混合的。
文獻[9]定理2證明周期點稠密的弱混合系統是初值敏感依賴的。本文定理2表明,周期點稠密性條件是可去的。文獻[5]說明非平凡的拓撲弱混合的系統是multi-敏感的。但是未有證明,為保證本文完整性,給出該結果的詳細證明。
定理2如果動力系統(X,f)是弱混合的,則(X,f)是multi-敏感的。特別地,(X,f)是初值敏感依賴的。
證明由定理1知,只須證明拓撲弱混合蘊含multi-敏感性。事實上,由于X為非平凡的空間,所以存在不同的兩點x,y∈X。取ε=d(x,y)/4>0,同時取V1=B(x,ε),V2=B(y,ε)。顯然,
dist(V1,V2)=inf{d(z1,z2):z1∈V1,z2∈V2}≥2ε
對任意自然數n,任取n個非空開子集U1,…,Un?X,同時令
U=U1×U1×U2×U2×…×Un×Un?X2n,V=V1×V2×V1×V2×…×V1×V2?X2n
由于f是拓撲弱混合的,由引理1知f(×2n)是拓撲傳遞的,因此存在m∈Z+,使得
(f(×2n))m(U)∩V≠φ
這說明對任意1≤i≤n,
fm(Ui)∩V1≠φ≠fm(Ui)∩V2
所以diam(fm(Ui))≥2ε,因此,(X,f)是multi-敏感的。
[1] LI T Y,YORKE J A.Period three implies chaos[J].Amer Math Monthly,1975,82:985-992.
[2] DEVANEY R L.An introduction to chaotic dynamical systems[M].Reading:Addison-Wesley,1989.
[3] BANKS J,EROOKS J,CAIRNS G,et al.On Devaney’s definition of chaos[J].Amer Math Monthly,1992,99:332-334.
[4] GLASNER E,WEISS B.Sensitive dependence on initial conditions [J].Nonlinearity,1993,6:1067-1075.
[5] MOOTHATHU T K.Stronger forms of sensitivity for dynamical systems[J].Nonlinearity,2007,20:2115-2126.
[6] WU X,WANG J,CHEN G.F-sensitivity and multi-sensitivity of hyperspatial dynamical systems[J].J Math Anal Appl,2015,429:16-26.
[7] 葉向東,黃文,邵松.拓撲動力系統概論[M].北京:科學出版社,2008.
[8] XU Z J,LIN W,RUAN J.Decay of correlations implies chaos in the sense of Devaney[J].Chaos,Solitons and Fractals,2004,22:305-310.
[9] 王濤,賈諾.Devaney混沌的隨機性質[J].數學的實踐與認識,2010,40:210-213.
[10] 吳新星,朱培勇.關于連續區間映射的敏感依賴性[J].系統科學與數學,2012(32):215-225.
[11] 吳新星.關于d-跟蹤性質的一些注記[J].中國科學:數學,2015,45:273-286.
[12] 馮漢,索宇,朱培勇.基于Logistic映射的迭代式的混沌特性及混沌控制[J].四川理工學院學報:自然科學版,2011,25(1):24-26.
[13] 盧天秀,朱培勇.線性序拓撲空間上不穩定流形的映射性質[J].四川理工學院學報:自然科學版,2009,23(4):32-34.
[14] 李瑞佳,朱培勇.拓撲動力系統中強傳遞集的一些性質[J].四川理工學院學報:自然科學版,2016,29(6):90-93.
[15] WALTERS P.An Introduction to Ergodic Theory[M].New York:Springer-Verlap Inc.,1982.
Further Study on Stochastic Properties in Devaney’s Chaos
ZHANGXinmin
(School of Sciences, Southwest Petroleum University, Chengdu 610500, China)
The relations among some dynamical properties (for example, weakly mixing, topologically weakly mixing, and sensitivity) are main research for dynamical systems. It is proved that every weakly mixing dynamical system defined using correlation function is topologically weakly mixing. Based on this result, it is obtained that such a system is multi-sensitive and sensitively dependent on initial conditions, improving the main results obtained by Wang Tao and Jia Nuo in 2010.
weakly mixing; topologically weakly mixing; multi-sensitivity
2017-04-11
國家自然科學基金(11601449);四川省教育廳科學研究基金(14ZB007)
張新敏(1988-),女,重慶榮昌人,講師,碩士,主要從事拓撲動力系統方面的研究,(E-mail)zhangxinmin1995@163.com
1673-1549(2017)03-0094-03
10.11863/j.suse.2017.03.19
O189.1
A

