基于Lotka—Volterra的新醫藥制藥企業的市場分析
湯婉儀


摘 要 隨著新型禽流感病毒H7N9的出現,新醫藥的研發也成了抑制病菌傳播的重中之重。本文從新醫藥的制藥企業之間的競爭與合作活動分析的基礎上,基于Lotka-Volterra模型的思想,建立新醫藥制藥企業之間的競爭與合作模型,并用古諾模型分析其利潤。
關鍵詞 新醫藥的制藥 Lotka-Volterra模型 競爭與合作 古諾模型
一、引言
由于新型病毒H7N9的出現,傳統的醫藥已無法起到對新型病毒的抑制和預防作用,所以市場對治愈H7N9的新醫藥的需求是刻不容緩的。然而醫藥研發單位配制好新藥方以后,要選擇高技術的制藥單位,這樣各個制藥單位在爭取只要名額時就會有一定的競爭。但需要考慮到的是,新醫藥的制藥企業之間的活動多與高技術相關,他們更加注重知識和技術的共享合作,而由于高技術的高滲透性和擴散性,新醫藥的制藥企業可以更加方便快捷的實現競爭與合作。另一方面,制藥企業的品牌因素以及企業的市場占有率的影響,也需要考慮其中。然而,新醫藥也具有與其他新型高技術產品相同的體積小、標準規范、便于運輸的特點,而新醫藥的研制也有其自身的市場需求,所以一旦上市其利潤情況也是可觀的。
二、模型的建立
針對研制H7N9新醫藥的制藥企業之間表現出的“先竟后合”的關系,本文借助改造后的Lotka-Volterra模型分析其協調關系,采用古諾模型分析基于古諾的競爭均衡及其利潤產出。
LV模型由數學家Lotka和Volterra提出,最初用來模擬生態學中種群的動態變化關系,描述多種群對資源的競爭關系以及相互共存模式。近年來,在經濟研究中也開始有所應用,但大部分結論僅僅局限于經濟增長以及社會人口控制等宏觀問題。隨著H7N9這類新型病毒的出現,市場對新醫藥的需求刻不容緩,所以結合現實生活,對新醫藥的制藥企業之間的競爭分析是很有必要的。
古諾模型是有Cournot提出的,該模型假設企業之間互相無勾結行為,但互相知道對方怎樣行動,從而各自怎樣確定最優產量來實現利潤最大化。與其他競爭模型相比,Cournot模型對同質產品產量競爭的分析比較深入,能夠計算出競爭的均衡利潤。
三、模型分析
(一)基于古諾模型的競爭均衡模型
在新醫藥的藥方配好之后,為確定其制藥企業,往往會選擇高技術的生產廠家,被選定的生產廠家之間就形成動態的市場寡占結構。基于上述分析,本文選用Cournot模型分析新醫藥的制藥企業在競爭制藥名額過程中的競爭關系,并計算競爭的均衡利潤。
根據Cournot模型,假設xi是企業i的利潤函數,yi是企業i的產量,ci是企業i的成本函數,Q是市場總需求量,P()是價格函數,用線性函數表示需求P()
=Q-。
企業的利潤模型為xi=yi·P()-ci(yi)即利潤=產量×價格-成本。
(二)基于Lotka-Volterra的企業協調模型
假設存在新醫藥的制藥企業集群η,η使企業之間合作的范圍更廣,競爭更激烈。假設η中有甲、乙兩個高技術企業,設為x1、x2,t表示時間,、是企業甲、乙所擁有的市場占有率變化,A1、A2分別表示甲、乙企業市場占有率的自然增長率,由于高技術和知識具有短循環的特點,所以制藥企業的高技術的生命周期對制藥企業的市場占有率非常重要,因此設B1、B2分別為甲、乙制藥企業的高技術生命周期對市場占有率的影響系數,C1、C2為擁有高技術的制藥企業x1、x2對高技術和知識的應用及研制新藥的能力,設α和β是兩種高技術,K1是企業x1、x2對α、β的高技術的需求,D1、D2表示制藥企業x1、x2的品牌影響力。E12和E21分別為企業x2對x1和企業x1對x2的相互影響系數,θ1、θ2表示制藥企業x1、x2在合作與競爭活動中所產生的作用系數,則可得以下模型。
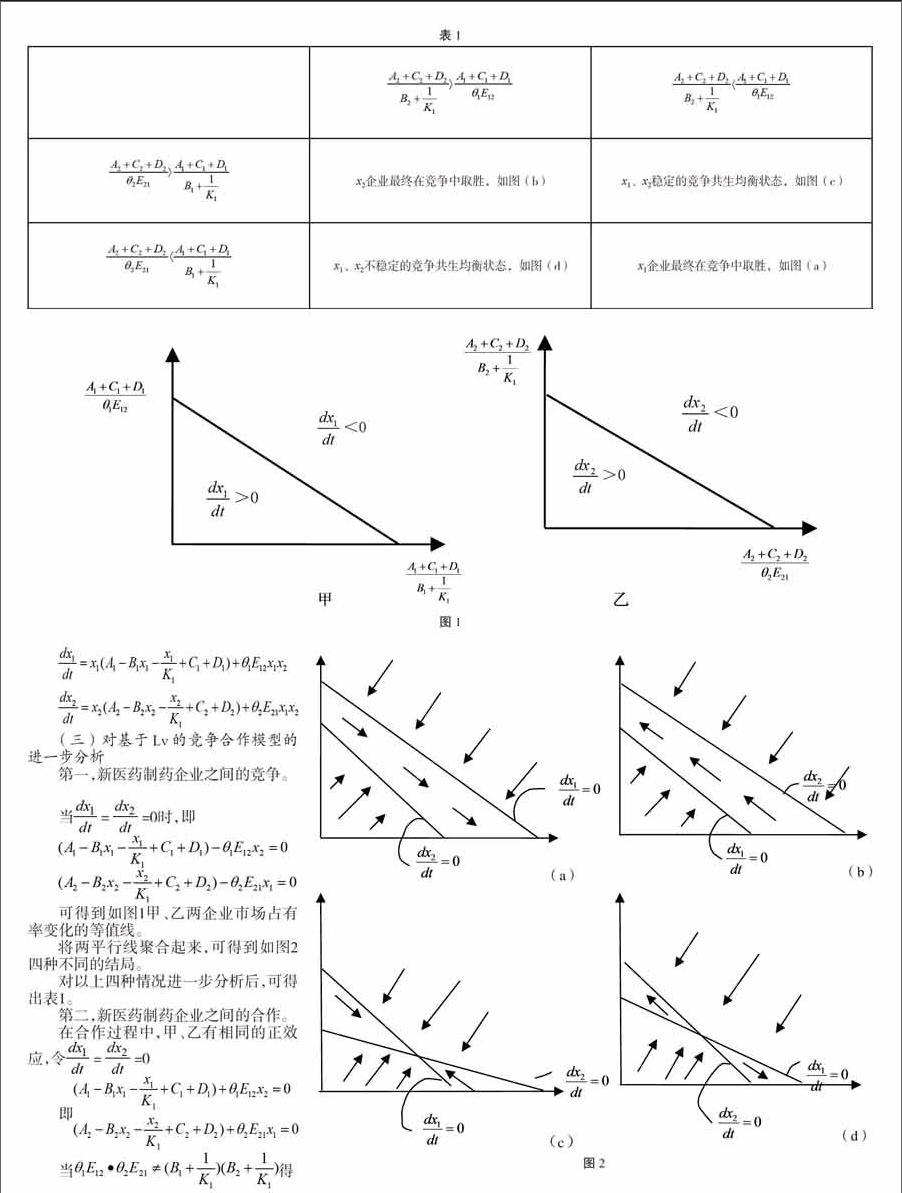
當即時,甲、乙兩制藥企業達到互利共生的穩定狀態。但由于受市場需求量的限制以及高技術的周期性的影響,x1、x2企業最終會達到一個飽和值,平衡終將被打破。
四、模型的擴展
由于新醫藥制藥企業存在參差不齊的制藥技術,η產業集群中存在著多個相互關聯、相互影響、相互競爭與合作的制藥企業,它們錯綜復雜,共同構成一個復雜的系統,所以結合實際情況,我們將模型擴展到更為一般的情況。
設制藥企業共擁有m種高科技制藥技術,有N個企業同時競爭H7N9新醫藥的研制。xr是xi企業掌握的第r種核心技術,Eijr是xi和xj在r種技術上的相互影響系數,mi表示i企業掌握的核心高技術數目。則模型可推廣到如下多維的情形:
多個新醫藥制藥企業的協調關系更為復雜,但企業間基本的合作與競爭規律與前文討論基本一致,在此不多做解釋。
五、結語
本文利用cournot競爭模型計算新醫藥制藥企業的博弈產量,并運用Lv模型建立新醫藥制藥企業的競爭與合作的協調模型,并結合圖形分析,得到了以下結論:
第一,新醫藥制藥企業之間競爭后有以下結果:其中一方勝出或相互之間穩定的競爭共生及不穩定的競爭共生狀態。
第二,當滿足 時,新醫藥制藥企業達到短暫的互利共生的穩定狀態,但由于受到市場需求量以及高技術周期等的影響,最終會打破平衡。
基于市場需求及高技術的研發水平,新醫藥制藥企業可能需要和其他產業進行競爭和合作等活動,此類復雜問題的分析,是今后還需研究的問題。
(作者單位為湖北大學楚才學院)
參考文獻
[1] 龍躍,易樹平.基于Lotka-Volterra的汽車零部件橫向企業協調決策分析[J].科研管理,2009(03):67-73.
[2] 高長元,杜鵬.基于Lotka-Volterra的高技術虛擬產業集群成員間合作與競爭模型[J].科技進步與對策,2009(23):72-75.

