如何利用函數的單調性解題

■陜西省西鄉縣第二中學 閆 俊

如何利用函數的單調性解題

■陜西省西鄉縣第二中學 閆 俊

函數的單調性是函數的重要性質之一,也是高考考查函數時重點考查的內容。在高考試題中我們通常見到的函數單調性的應用不外乎求參數的取值范圍、解不等式與求函數的最值這三類問題。應當強調的是,解決這三類問題時應當重視函數單調性的定義、函數的定義域,以及數形結合思想。

一、利用函數的單調性求參數的取值范圍

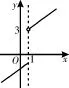
圖1

解析:若設g(x)=(a-2)x-1,h(x)= x+2。因為函數f(x)在(-∞,+∞)上單調遞增,所以a-2>0,即當a>2時,g(x)在(-∞,1]上單調遞增。而在(1,+∞)上h(x)也是單調遞增的,于是h(x)>h(1)=3。要使函 數 f (x) =在(,-∞ +∞)上單調遞增,如圖1所示,則需g(1)≤h(1),即a-3≤3,所以a≤6。綜上,實數a的取值范圍是2

評注:由以上解題過程可以看出,對含參數的分段函數利用其單調性求參數的取值范圍,應抓住兩點:一是嚴格遵循函數單調性的定義;二是結合函數圖像觀察約束參數的限制條件,也就是關于參數的不等式。

二、利用函數的單調性解不等式

首先,要做一下強調,如果是利用函數的單調性解不等式,則一定要注意函數的定義域,否則極易出現錯解。

已知函數f(x)是增函數,定義域為(0,+∞),且f(4)=2,f(xy)=f(x)+ f(y),求滿足f(x)+f(x-3)≤2的x的取值范圍。

解析:因為f(x)+f(x-3)≤2,f(xy)= f(x)+f(y),所以f[x(x-3)]=f(x)+ f(x-3)≤2=f(4)。又f(x)在(0,+∞)上是增函數,所以x(x-3)≤4,解得-1≤x≤4。由題意知,滿足f(x)+f(x-3)≤2,則即解得3

評注:函數的單調性是相對于函數定義域內某個子區間而言的“局部”性質,它反映了函數在某區間上函數值的變化趨勢。當我們利用函數的單調性解決問題時,如果不顧函數的定義域去盲目解題,就會造成錯解。

三、利用函數的單調性求函數的最值

評注:函數單調性在解答過程中的運用主要體現在通過題設所給函數等價變形為,把原問題轉化為對函數單調性的討論,明確單調性后利用單調性達到求解最值的目的。

(責任編輯 王福華)