利用帶形狀參數的有理勢函數構造基于Metaball的過渡曲線
李軍成, 宋來忠
(1. 湖南人文科技學院 數學與金融學院, 湖南 婁底 417000; 2. 三峽大學 理學院, 湖北 宜昌 443002)
利用帶形狀參數的有理勢函數構造基于Metaball的過渡曲線
李軍成1, 宋來忠2
(1. 湖南人文科技學院 數學與金融學院, 湖南 婁底 417000; 2. 三峽大學 理學院, 湖北 宜昌 443002)
利用現有勢函數構造基于Metaball的過渡曲線,此過渡曲線無法兼具擬高階連續性與形狀可調性. 針對這一問題, 巧妙地從一種帶形狀參數的曲線模型出發, 構造一類帶形狀參數的有理勢函數, 并研究該勢函數的性質. 所構造的有理勢函數具有統一的數學模型, 不僅能使過渡曲線在端點處達到擬Ck連續, 而且還可通過修改形狀參數的值調整過渡曲線的形狀. 實例表明,通過調整有理勢函數的次數及形狀參數的取值可構造出滿足不同擬連續性且形狀不同的過渡曲線, 以滿足實際應用需要.
勢函數; 形狀參數; Metaball技術; 過渡曲線; 形狀調整
Journal of Zhejiang University(Science Edition), 2017,44(3):307-313
在計算機輔助幾何設計(CAGD)中, 曲線造型一直以來都是重要的研究課題. 隨著幾何造型工業的發展, 人們往往需要改變曲線的形狀以滿足實際工程的需要. 因此, 帶形狀參數的曲線造型方法逐漸成為研究熱點. 這些方法的主要目的是在曲線模型中引入形狀參數, 并通過修改形狀參數的取值實現對曲線形狀的調整. 例如, 帶形狀參數的Bézier曲線[1-2], 帶形狀參數的B樣條曲線[3-4], 帶形狀參數的三角曲線[5-6]等.
在曲線造型中, 過渡曲線的構造在許多實際工程問題中有著十分廣泛的應用[7-9]. 為滿足過渡曲線的設計要求, 李凌豐等[10]提出了一種基于勢函數與Metaball技術構造過渡曲線的方法, 該法采用WYVILL等定義的六次多項式勢函數構造能光滑連接2條曲線的過渡曲線, 雖然對被連接曲線的種類沒有限制, 但所構造的過渡曲線在端點處的連續性較低,且其形狀無法調整. 為解決此問題, 高暉等[11]構造了2類勢函數: 第1類為可使過渡曲線在端點處達到擬Ck連續的多項式勢函數; 第2類為可使過渡曲線在端點處達到擬C1連續且具有形狀可調性的混合三角勢函數. 文獻[11]構造的第1類勢函數,雖然提高了過渡曲線在端點處的擬連續性, 但仍然無法調整其形狀; 構造的第2類勢函數,雖然過渡曲線的形狀可調, 但在端點處的擬連續性較低. 另外, 2類勢函數構造過程較為煩瑣,且均無統一的數學模型, 因此需要重新構造滿足不同情形的勢函數. 與文獻[10-11]類似, 劉華勇等[12-14]研究了基于調配函數的過渡曲線構造與連續性問題, 并給出了可使過渡曲線在兩端點處滿足擬Ck(k=0, 1, 2)連續的調配函數. 注意到為了使過渡曲線在滿足一定連續性的條件下同時具有形狀可調性, 文獻[12-14]將2條被過渡曲線取為帶形狀參數的曲線模型. 由于所選取的2條被過渡曲線均帶有形狀參數, 所以所構造的過渡曲線在不改變幾何連續性的情形下,可通過其所帶的形狀參數進行形狀調整. 然而, 在大量實際過渡曲線構造問題中, 2條被過渡曲線的模型往往并不特定. 為此, 李軍成等[15]構造了一類帶參數的多項式勢函數, 并研究了該勢函數在構造過渡曲線中的應用. 雖然文獻[15]提出的方法對2條被過渡曲線的種類沒有限制, 而且還可利用勢函數所帶的參數對過渡曲線的形狀進行調整, 但所構造的過渡曲線在兩端點處僅能滿足擬C2連續, 不適合連續性要求更高的場合.
為滿足更高要求的過渡曲線設計, 本文在文獻[15]的基礎上, 巧妙地從一種帶形狀參數的曲線模型出發, 構造一類帶形狀參數的有理勢函數, 該勢函數不僅具有統一的數學模型, 而且可使過渡曲線同時具有擬Ck(k≥1)連續性和形狀可調性.
1 問題的描述
在解決大量實際工程問題的過程中, 常常需要將數段零散的曲線段連接成一個整體, 且要求不破壞曲線段的光滑度, 基于 Metaball 的過渡曲線構造就能滿足這一要求[10]. 文獻[10-11]描述了基于Metaball構造過渡曲線的問題: 給定平面上相交于點C的2條參數曲線P(t)與Q(t), 2條曲線的端點分別記為A與B, 如圖1所示, 希望構造1條能光滑連接A和B點的過渡曲線R(t).
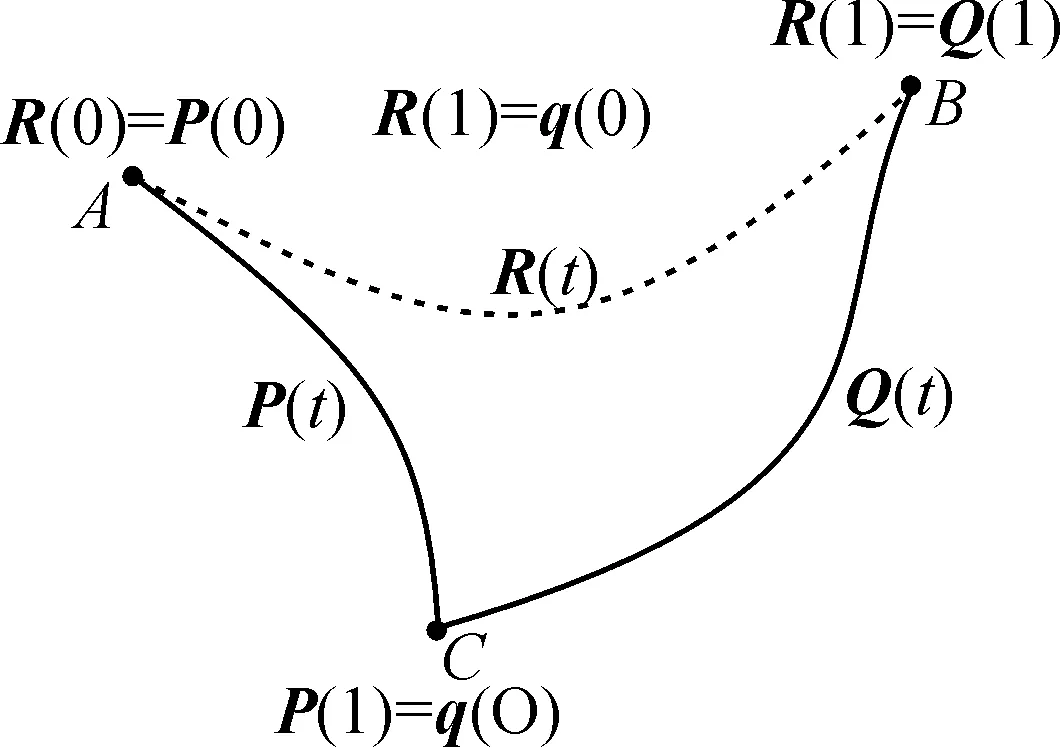
圖1 構造基于Metaball的過渡曲線Fig.1 Construction of transition curves basedon Metaball technique
針對上述問題,文獻[11]給出了過渡曲線的方程:
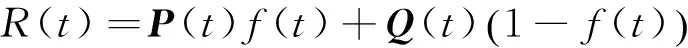
(1)
其中,0≤t≤1,f(t)為勢函數.
由式(1)可知,為使所構造的過渡曲線在2個端點處達到擬Ck連續,勢函數f(t)(0≤t≤1)在端點處須滿足
(2)
由于構造過渡曲線R(t)的目的是使曲線P(t)連續平滑地過渡到Q(t),因此過渡曲線R(t)在靠近曲線P(t)處應與P(t)具有相似的形狀,而在靠近曲線Q(t)處則應與Q(t)具有相似的形狀.由式(1)可知,當給定曲線P(t)與Q(t)時,過渡曲線R(t)的形狀完全由勢函數f(t)決定,故勢函數的選取是構造過渡曲線的關鍵.本文的主要目的就是構造一類同時具有多種特性的勢函數,并將其用于構造基于Metaball的過渡曲線.
2 勢函數的構造及其性質
2.1 勢函數的構造
構造勢函數的主要思想:首先選取一種恰當的帶形狀參數的曲線模型,然后利用曲線模型在端點處滿足性質來構造具有某種特定要求的勢函數.
文獻[16]構造了一種帶5個參數k,ωi,αi(i=1,2)的曲線,其表達式為

(3)
其中,0≤t≤1,Vi∈Rd(d=2,3;i=0,1,2,3)為給定的控制頂點,bi(t)(i=0,1,2,3)為調配函數,滿足
(4)
其中,
R(t)= (1-t)k+1+ω1(1-t)k+1t+
ω2(1-t)tk+1+tk+1,
整數k≥1,實數ωi>0(i=1,2),α1∈[0,1),α2∈(0,1].
由式(3)定義的曲線在端點處滿足
(5)
其中,1≤i≤k,Ai是與i,ω1,α1有關的常數,Bi是與i,ω2,α2有關的常數.
顯然,式(3)對應的函數可表示為
f(t)=b0(t)y0+b1(t)y1+b2(t)y2+b3(t)y3,
(6)
其中,bi(t)(i=0,1,2,3)為由式(4)定義的4個調配函數,yi∈R(i=0,1,2,3).
由式(5)可知,式(6)定義的函數在端點處滿足
(7)
為了使所構造的過渡曲線在2個端點處達到擬Ck連續,由式(2)和(7)則可得
(8)
由式(8)可得
(9)
將式(9)代入式(6),并令ω1=ω2=ω,可定義如下一類帶形狀參數的有理勢函數.
定義1 對于整數k≥1,實數ω>0,稱關于變量t(0≤t≤1)的函數
(10)
為帶形狀參數ω的有理勢函數.
2.2 勢函數的性質
帶形狀參數ω的有理勢函數fk(t)具有如下性質:
性質1 端點性:勢函數fk(t)在端點處滿足
fk(0)=1,fk(1)=0,
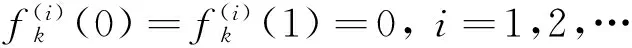
證明 由勢函數fk(t)的構造過程可知,端點性顯然成立.
注1 由性質1及式(1)可得R(0)=P(0),R(1)=Q(1).此即表明,在端點A處,僅曲線P(t)對過渡曲線R(t)有影響;而在端點B處,僅曲線Q(t)對過渡曲線R(t)有影響.
另外,由性質1和式(1)并經簡單推導可得R(i)(0)=P(i)(0),R(i)(1)=Q(i)(1),i=1,2,…,k.表明勢函數fk(t)可使過渡曲線R(t)在兩端點處達到擬Ck(k≥1)連續.例如,使過渡曲線在兩端點處分別達到擬C1,C2,C3連續的勢函數為
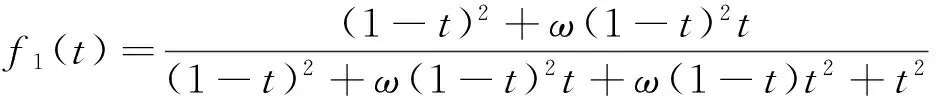

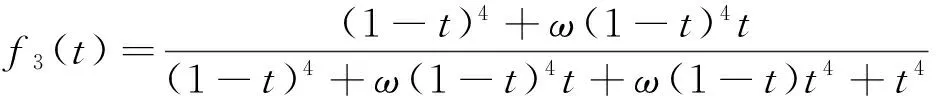
性質2 中點性:fk(0.5)=0.5.
證明 由式(10)可得
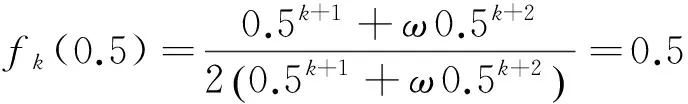
注2 由性質1及式(1)可得
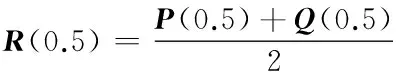
表明在t=0.5處,曲線P(t)與Q(t)對過渡曲線R(t)有相同的影響.
性質3 對稱性:fk(t)+fk(1-t)≡1.
證明 由式(10)可得
(11)
故由式(10)與式(11)易得
fk(t)+fk(1-t)≡1.
性質4 單調性:固定k與ω時,勢函數fk(t)關于變量t單調遞減.
證明 令

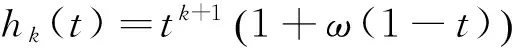
固定k與ω時,由式(10)經計算可得
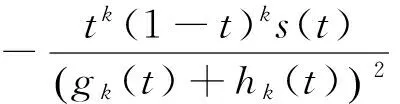
(12)
其中,
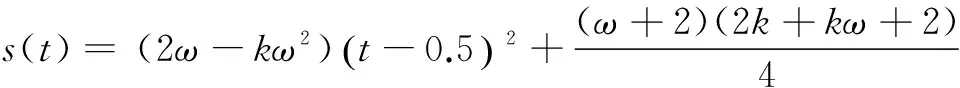
(13)
當k≥1,ω>0時,由式(13)可得
(14)
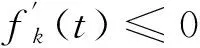

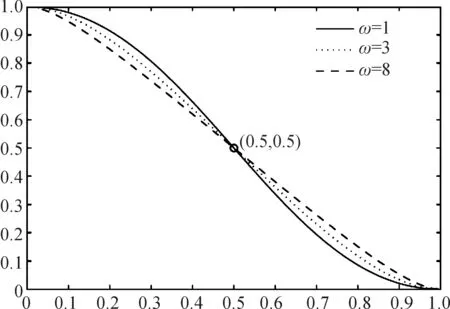
圖2 ω=2時的勢函數fk(t)(k=1,2,3)Fig.2 The potential function fk(t)(k=1,2,3) with ω=2
注3 由性質4及式(1)可知,隨著t(0≤t≤1)的增大,曲線P(t)對過渡曲線R(t)的作用逐漸減小,而曲線Q(t)對過渡曲線R(t)的作用則逐漸增大.
性質5 形狀可調性:固定k,當0≤t≤0.5時,勢函數fk(t)關于參數ω單調遞減;當0.5 證明 令 固定k與t,由式(10),計算得 (15) 圖3 參數ω取不同值時的勢函數f1(t)Fig.3 The potential function f1(t) with different values of the parameter ω 注4 由性質5知,可通過修改參數ω(ω>0)的值調整勢函數fk(t)的形狀.于是,由式(1)知,當曲線P(t)與Q(t)保持不變時,過渡曲線在兩端點處滿足擬Ck(k≥1)連續的情形下,可通過修改參數ω的值對其形狀進行調整. 綜上所述,本文所構造的有理勢函數fk(t)不僅與文獻[10-15]中的勢函數或調配函數性質完全相同,而且還具有以下特性: (1)可令過渡曲線在兩端點處達到擬Ck(k≥1)連續. (2)具有統一的數學模型. 相對于文獻[10-15]給出的勢函數或調配函數,本文構造的有理勢函數fk(t)具有如下優勢: (1)文獻[10]所采用的勢函數雖然結構簡單,但所構造的過渡曲線在端點處僅滿足擬C1連續,且無法調整過渡曲線的形狀.而有理勢函數fk(t)不僅可令過渡曲線在端點處達到擬Ck連續,而且過渡曲線的形狀還可通過所帶的形狀參數ω進行調整. (2)文獻[11]所構造的2k+1次多項式勢函數雖然可令過渡曲線在端點處達到擬Ck連續,但無法調節過渡曲線的形狀,且滿足不同連續性要求的勢函數都需要通過求解方程組重新獲得.而有理勢函數fk(t)不僅具有統一的數學模型,而且在令過渡曲線在端點處達到擬Ck連續的情形下仍可通過修改形狀參數ω的值實現對過渡曲線形狀的調整. (3)文獻[11]所構造的幾類三角混合勢函數雖然可令過渡曲線具有形狀可調性,但過渡曲線在兩端點處僅滿足擬C1連續.而有理勢函數fk(t)不僅可實現過渡曲線的形狀可調,而且還令過渡曲線在兩端點處達到擬Ck連續. (4)雖然文獻[12-14]所構造的調配函數可令過渡曲線同時具有形狀可調性和在兩端點處滿足擬Ck(k=0,1,2)連續性,但都是將兩被過渡曲線取為特定的帶形狀參數的曲線.而利用有理勢函數fk(t)構造過渡曲線時,不僅實現了形狀可調和擬Ck連續,而且兩被過渡曲線可取為任意參數曲線. (5)文獻[15]所構造的多項式勢函數,不僅對兩被過渡曲線的種類沒有限制,而且還可通過勢函數中所帶的參數調整過渡曲線的形狀,但過渡曲線在兩端點處僅滿足擬C2連續.而有理勢函數fk(t)不僅對兩被過渡曲線的種類沒有限制,而且在令過渡曲線在兩端點處達到擬Ck(k≥1)連續的情形下還可通過勢函數所帶的參數對其形狀進行調整. 給出以下幾種情形下,利用有理勢函數fk(t)構造基于Metaball過渡曲線的實例. (1)直線與直線間的過渡曲線 設兩直線P(t)與Q(t)的方程分別為 形狀參數ω取不同值時,分別利用有理勢函數fk(t)(k=1,2,3)構造滿足擬Ck(k=1,2,3)連續的不同形狀的過渡曲線,如圖4所示. 圖4 直線與直線間的過渡曲線Fig.4 The transition curve between straight lines (2)直線與圓弧間的過渡曲線 設直線P(t)與圓弧Q(t)的方程分別為 形狀參數ω取不同值時,分別利用有理勢函數fk(t)(k=1,2,3)構造滿足擬Ck(k=1,2,3)連續的不同形狀的過渡曲線,如圖5所示. 圖5 直線與圓弧間的過渡曲線Fig.5 The transition curve between straight line and arc (3)圓弧與圓弧間的過渡曲線 設兩圓弧P(t)與Q(t)的方程分別為 形狀參數ω取不同值時,分別利用有理勢函數fk(t)(k=1,2,3)構造滿足擬Ck(k=1,2,3)連續的不同形狀的過渡曲線,如圖6所示. 圖6 圓弧與圓弧間的過渡曲線Fig.6 The transition curve between arcs (4)直線與曲線間的過渡曲線 設直線P(t)與曲線Q(t)的方程分別為 形狀參數ω取不同值時,分別利用有理勢函數fk(t)(k=1,2,3)構造滿足擬Ck(k=1,2,3)連續的不同形狀的過渡曲線,如圖7所示. 圖7 直線與曲線間的過渡曲線Fig.7 The transition curve between straight line and curve (5)圓弧與曲線間的過渡曲線 設圓弧P(t)與曲線Q(t)的方程分別為 形狀參數ω取不同值時,分別利用有理勢函數fk(t)(k=1,2,3)構造滿足擬Ck(k=1,2,3)連續的不同形狀的過渡曲線,如圖8所示. 圖8 圓弧與曲線間的過渡曲線Fig.8 The transition curve between arc and curve (6)曲線與曲線間的過渡曲線 設兩曲線P(t)與Q(t)的方程分別為 形狀參數ω取不同值時,分別利用有理勢函數fk(t)(k=1,2,3)構造滿足擬Ck(k=1,2,3)連續的不同形狀的過渡曲線,如圖9所示. 圖9 曲線與曲線間的過渡曲線Fig.9 The transition curve between curves 上述實例表明,利用本文提出的帶形狀參數的有理勢函數構造基于Metaball的過渡曲線時,可通過選取勢函數的次數及形狀參數值獲得連續的、形狀不同的過渡曲線,過渡曲線形狀自然,且均可光滑地連接2條被過渡曲線,能滿足不同的實際應用需求. 為了滿足更高要求的過渡曲線設計,本文巧妙地利用一種帶形狀參數的曲線模型,構造了一類帶形狀參數的有理勢函數.所構造的勢函數不僅具有統一的數學模型,而且在利用該勢函數構造基于Metaball的過渡曲線時,可令過渡曲線達到擬Ck(k≥1)連續,還可通過修改形狀參數值調整過渡曲線的形狀. [1]YANLL,LIANGQF.AnextensionoftheBéziermodel[J]. Applied Mathematics and Computation,2011,218(6):2863-2879. [2] BASHIR U, ABBSA M, ALI J M. TheG2andC2rational quadratic trigonometric Bézier curve with two shape parameters with applications[J]. Applied Mathematics and Computation,2013,219(20):10183-10197. [3] 王文濤,汪國昭.帶形狀參數的均勻B樣條[J].計算機輔助設計與圖形學學報,2004,16(6):783-788. WANG W T, WANG G Z. Uniform B-spline with shape parameter[J]. Journal of Computer-Aided Design & Computer Graphics,2004,16(6):783-788. [4] 左傳桂,汪國昭.多形狀參數的四階均勻B樣條曲線設計[J].浙江大學學報:理學版,2007,34(4):401-404. ZUO C G, WANG G Z. Curve design of multi-parameter uniform B-spline blending function of order four[J]. Journal of Zhejiang University: Science Edition,2007,34(4):401-404. [5] HAN X L, ZHU Y P. Curve construction based on five trigonometric blending functions[J]. BIT Numerical Mathematics,2012,52(4):953-979. [6] 徐迎博,喻德生.帶形狀參數的二次三角Bézier曲線形狀分析[J].浙江大學學報:理學版,2013,40(1):35-41. XU Y B, YU D S. Shape analysis of quadratic trigonometric polynomial Bézier curves with a shape parameter[J]. Journal of Zhejiang University: Science Edition,2013,40(1):35-41. [7] 王健立,畢合春,劉奎豐.滾齒加工的齒輪齒根過渡曲線[J].機械傳動,2013,37(1):82-86. WANG J L, BI H C, LIU K F. Tooth root fillet curve of gear by hobbling[J]. Journal of Mechanical Transmission,2013,37(1):82-86. [8] 郭蓓,趙遠揚,李連生,等.旋葉式壓縮機的氣缸型線研究[J].西安交通大學學報,2003,37(3):256-259. GUO B, ZHAN Y Y, LI L S, et a1. Research on cylinder profile of rotary vane compressor[J]. Journal of Xi’an Jiaotong University,2003,37(3):256-259. [9] 宋立權,趙學科,李智成,等.任意缸體旋葉式壓縮機的葉片型線設計理論研究及應用[J].機械工程學報,2011,47(15):143-148. SONG L Q, ZHAO X K, LI Z C, et a1. Study and application of the designing theory of the vane profile for any rotary vane compressor[J]. Journal of Mechanical Engineering,2011,47(15):143-148. [10] 李凌豐,譚建榮,趙海霞.基于Metaball的過渡曲線[J].中國機械工程,2005,16(6):483-486. LI L F, TAN J R, ZHAO H X. Construction method of transition curve based on Metaball technique[J]. China Mechanical Engineering,2005,16(6):483-486. [11] 高暉,壽華好.勢函數的構造及基于Metaball的過渡曲線[J].計算機輔助設計與圖形學學報,2015,27(5):900-906. GAO H, SHOU H H. Construction of potential function and transition curve based on Metaball technique[J]. Journal of Computer-Aided Design & Computer Graphics,2015,27(5):900-906. [12] 劉華勇,張大明,李璐.基于參數連續HCBézier-like曲線的過渡曲線的構造[J].純粹數學與應用數學,2011,27(1):69-74. LIU H Y, ZHANG D M, LI L. Constructing of blending HC Bézier-like curve preserving continuity[J]. Pure and Applied Mathematics,2011,27(1):69-74. [13] 劉華勇,張大明,李璐,等.幾何連續的Bézier-like曲線的形狀調配[J].山東大學學報:理學版,2012,47(3):51-55. LIU H Y, ZHANG D M, LI L, et al. Shape blending Bézier-like curve with geometric continuity[J]. Journal of Shandong University: Natural Science,2012,47(3):51-55. [14] 劉華勇,段小娟,張大明,等.基于三角Bézier-like的過渡曲線構造[J].浙江大學學報:理學版,2013,40(1):42-46. LIU H Y, DUAN X J, ZHANG D M, et al. Constructing of blending trigonometric Bézier-like curve[J]. Journal of Zhejiang University: Science Edition,2013,40(1):42-46. [15] 李軍成,宋來忠,劉成志.帶參數的多項式勢函數與構造基于Metaball的過渡曲線[J].中國圖象圖形學報,2016,21(7):893-900. LI J C, SONG L Z, LIU C Z. The polynomial potential function with a parameter and transition curve based on Metaball technology[J]. Journal of Image and Graphics,2016,21(7):893-900. [16] 嚴蘭蘭,韓旭里.形狀及光滑度可調的自動連續組合曲線曲面[J].計算機輔助設計與圖形學學報,2014,26(10):1654-1662. YAN L L, HAN X L. Automatic continuous composite curve and surface with adjustable shape and smoothness[J]. Journal of Computer-Aided Design & Computer Graphics,2014,26(10):1654-1662. Construction of transition curves based on Metaball technique using rational potential function with a shape parameter. LI Juncheng1, SONG Laizhong2 (1.CollegeofMathematicsandFinances,HunanUniversityofHumanities,ScienceandTechnology,Loudi417000,HunanProvince,China; 2.CollegeofScience,ChinaThreeGorgesUniversity,Yichang443002,HubeiProvince,China) Using the existing potential functions to construct transition curve based on Metaball technique, it can not have both quasi high order continuity and shape adjustability. To solving this problem, a rational potential function with a shape parameter is constructed ingeniously from a curve with shape parameters. Some properties of the rational potential function are studied. The rational potential function is expressed as a unified mathematical model, which can not only make the transition curve achieve quasiCkcontinuity at the end points, but also adjust the shape of the transition curve by modifying the value of the shape parameter. Some examples showed that the transition curves with different continuities and shapes could be constructed by changing the degree and the shape parameter of the rational potential function, which could be used to meet different needs of the practical application. potential function; shape parameter; Metaball technique; transition curve; shape adjustment 2016-01-26. 國家自然科學基金資助項目(11171181);湖南省教育廳資助科研項目(14B099). 李軍成(1982-),ORCID:http://orcid.org/0000-0002-1904-4068,男,博士,副教授,主要從事計算機輔助幾何設計及其應用研究,E-mail:lijuncheng82@126.com. 10.3785/j.issn.1008-9497.2017.03.011 TP 391 A 1008-9497(2017)03-307-07
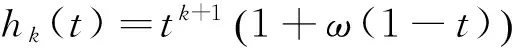
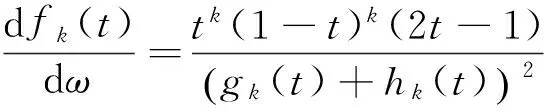

3 應用實例
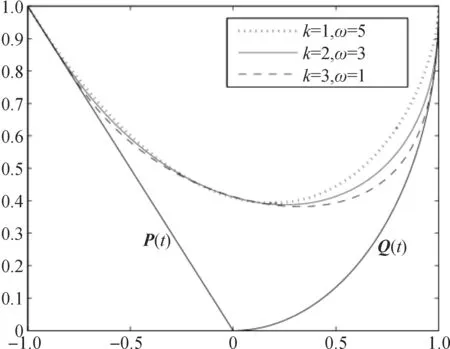
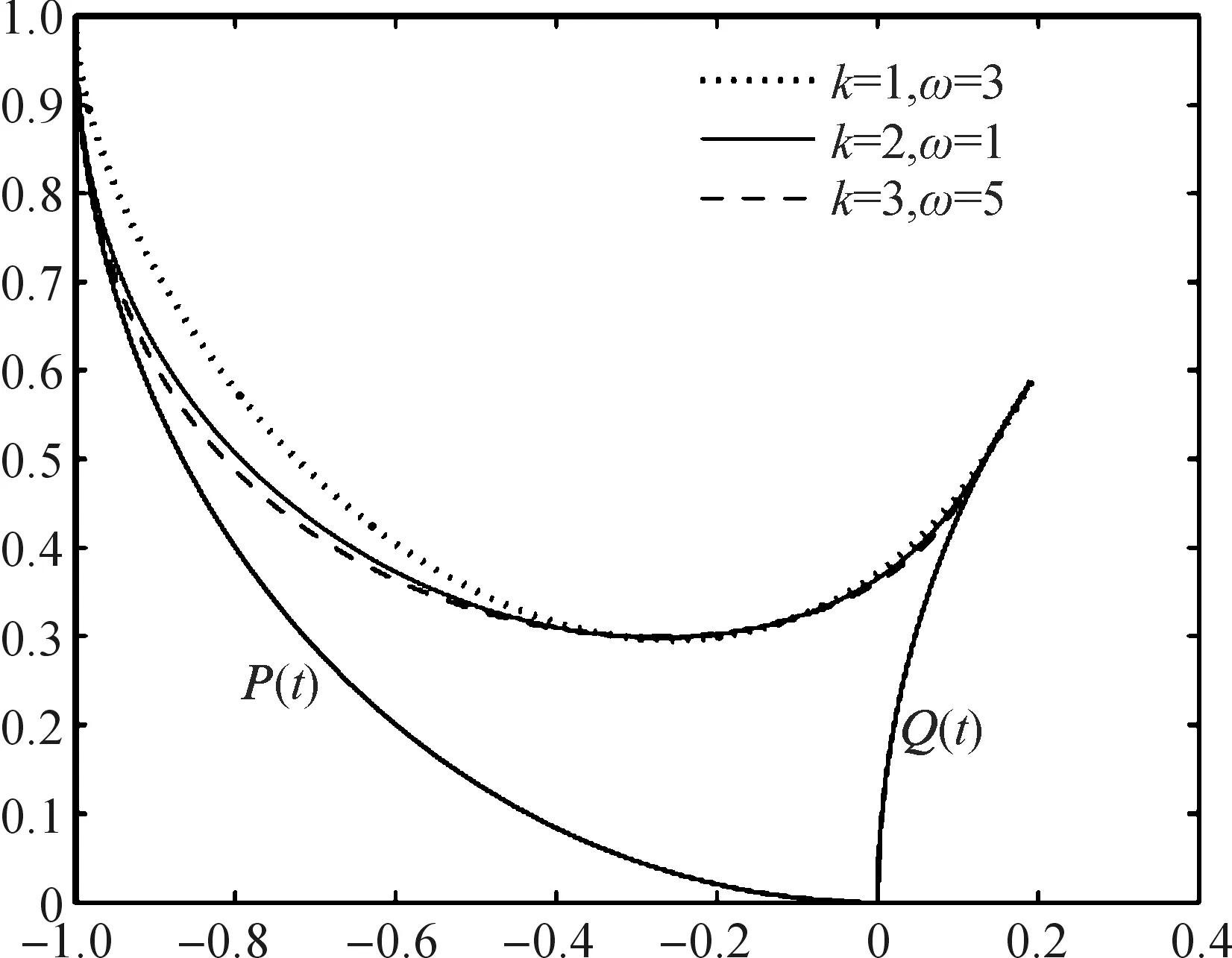
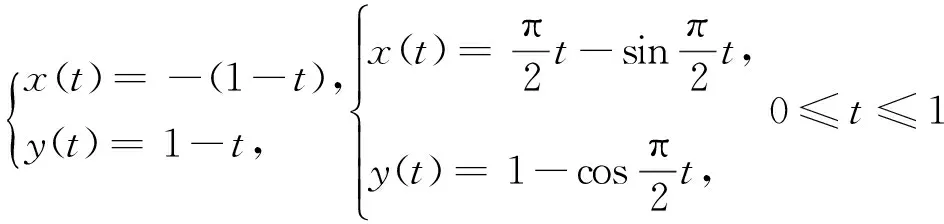
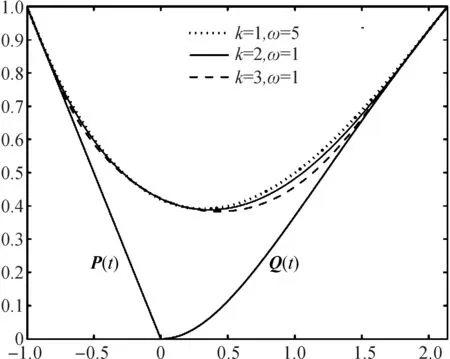
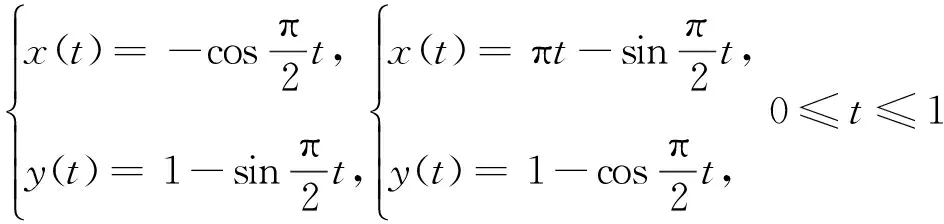
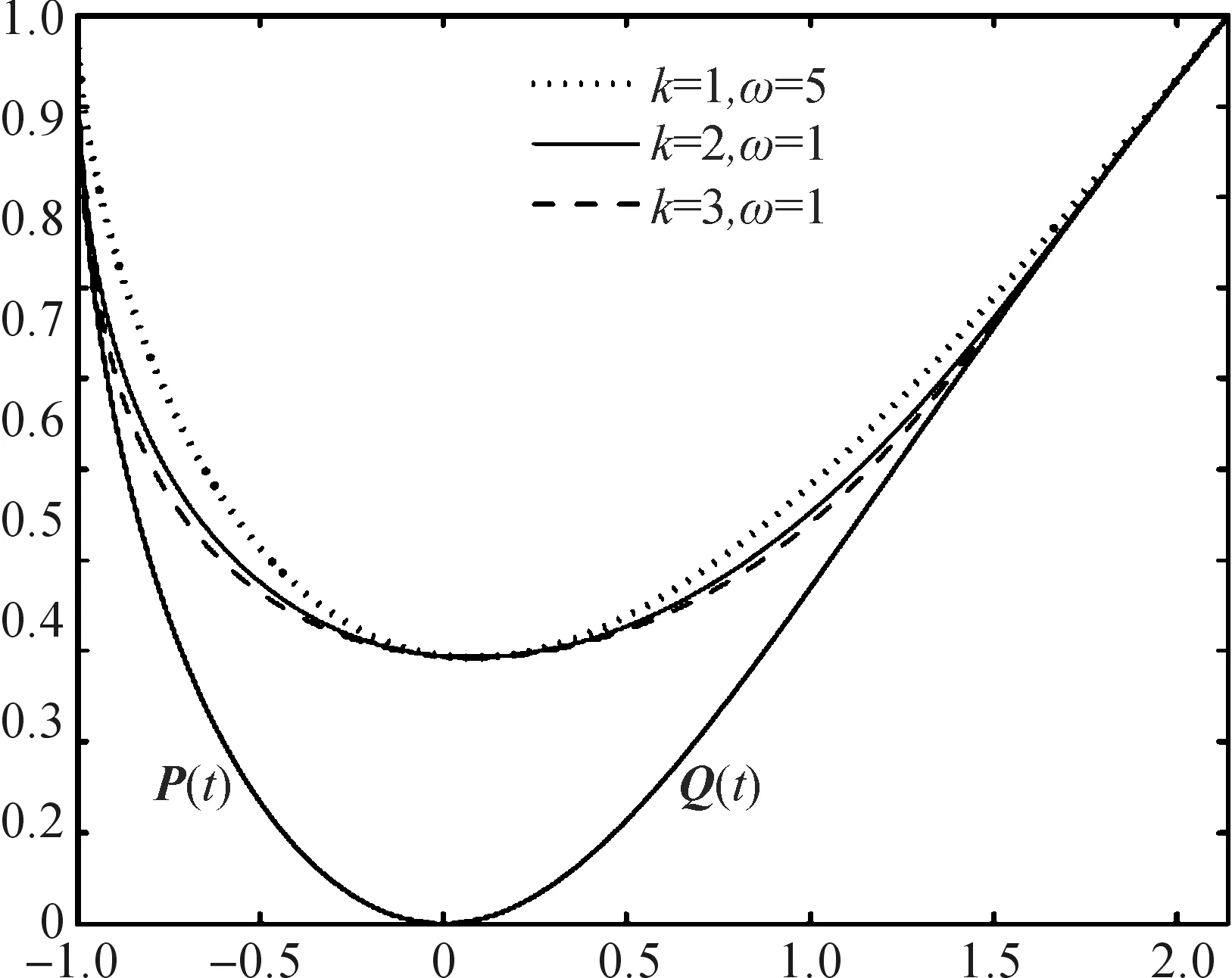
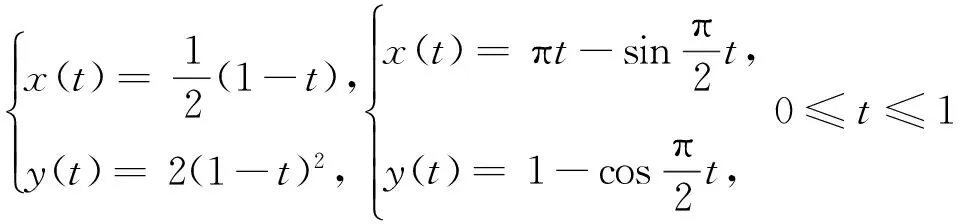

4 結 語


