具有死區輸入的分數階多渦卷混沌系統的有限時間同步

毛北行， 孟曉玲

(鄭州航空工業管理學院 理學院， 河南 鄭州 450015)

具有死區輸入的分數階多渦卷混沌系統的有限時間同步

毛北行， 孟曉玲

(鄭州航空工業管理學院 理學院， 河南 鄭州 450015)

基于滑模控制研究了具有死區輸入的分數階多渦卷系統的有限時間同步問題，根據分數階微積分的相關理論，給出了系統取得同步的充分性條件，結果表明：在一定條件下，分數階多渦卷混沌系統可取得有限時間同步.

分數階；多渦卷系統；滑模；混沌同步

Journal of Zhejiang University(Science Edition), 2017,44(3):302-306

0 引 言

近年來混沌同步問題引起了控制界的廣泛關注[1-8]，分數階混沌系統逐漸成為研究熱點，例如：孫寧等[9]研究了分數階不確定混沌系統的滑模投影同步問題，實現了主從系統的投影同步.余明哲等[10]研究了一類分數階不確定混沌系統的自適應滑模同步問題，實現了驅動系統與響應系統的快速同步.仲啟龍等[11]基于主動滑模控制方法研究了分數階混沌系統的同步控制問題.而多渦卷系統密匙參數更多，因而在混沌通信中得到了廣泛應用.例如：孫美美等[12]研究了一類多渦卷超混沌系統的同步控制問題,提出了一種自適應滑模控制方案.利用滑模控制和自適應控制技術,消除了系統不確定性和未知擾動的影響.劉恒等[13]研究了含擾動的多渦卷系統的修正函數時滯投影同步，得到了系統取得同步的充分性條件.這些工作大多是研究分數階系統的混沌同步，然而工程和實際應用中更需要研究分數階混沌系統的有限時間同步問題.例如：毛北行等[14]研究了一類分數階復雜網絡混沌系統的有限時間同步問題，并估計了系統取得混沌同步所需的時間.在設計和植入控制器時，不能忽略具有死區的非線性輸入.田小敏等[15]研究了具有死區輸入的混沌系統的有限時間同步問題，證明了滑模階段和趨近階段均是有限時間收斂的.本文基于滑模控制并利用分數階微積分的相關理論，研究了具有死區輸入的分數階多渦卷系統的有限時間同步問題，以得到系統取得有限時間同步的充分性條件.

n-1<α≤n∈Z+.

1 主要結果

設計如下一類分數階多渦卷混沌系統作為主系統：

(1)

其中，x1,x2,x3∈R3為系統的狀態變量，α,β為系統參數，f(x1)為非線性項，f(x1)=sin(ax1-bx1|x1|-(cx1)3)，當α=0.3,β=5.1,a=11,b=1.6,c=0.4,q=0.873時出現混沌吸引子，其對應的從系統為：

(2)

其中，hi(ui(t))是死區非線性輸入，定義如下：

hi(ui(t))=

其中，h+i(t),h-i(t)是ui(t)的非線性函數，u+i,u-i是給定的常數.

其中，β+i,β-i是正常數.

假設1 設不確定項Δfi(y)和外部擾動di(t)有界，即存在δi,ρi>0，使得

|Δfi(y)|<δi, |di(t)|<ρi.

定義系統誤差：

e1=y1-x1,e2=y2-x2,e3=y3-x3，

很容易得到誤差方程：

(3)

V1-η(t)≤V1-η(t0)-p(1-η)(t-t0),t0≤t≤T，

并且V(t)≡0,t≥T，其中,

設計滑模面

誤差系統滿足滑動面方程：

由此易得

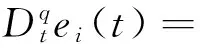
(4)

定理1 設計控制器：

(5)

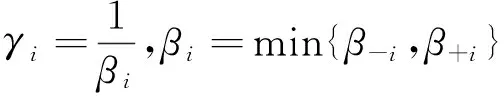
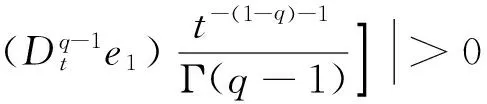
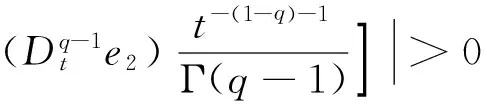
其中，

ki>0，σi=δi+ρi.

選取滑模面：

則系統的軌跡在有限時間T1內收斂到原點，其中，

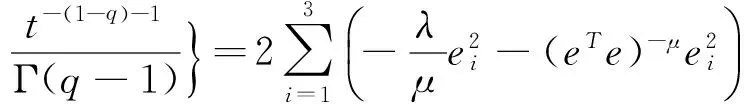
得到

兩邊同乘以e2λt，得到

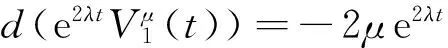
兩邊積分，得到

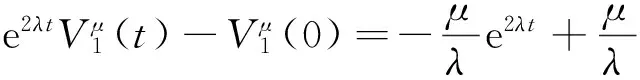
易得

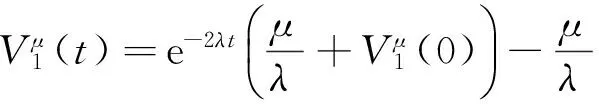
如果

將我院2017年10月-2017年12月收治的520例醫保患者視為研究對象,對其住院費用進行分析。全部患者中,男性患者271例,女性患者249例。年齡最大85歲,最小23歲,平均年齡(52.3±1.4)歲。疾病類型涵蓋了醫院各個科室系統。

則有

定理2 對誤差系統(3)，具有非線性死區輸入的控制器(5)，誤差系統的狀態軌跡能達到滑模面.

證明

(ui(t)-u+i)h+i(ui(t))=-γiζisgnsihi(ui(t))≥

-sgnsihi(ui(t))≥ζisgn2si，兩邊同乘以|si|，并考慮到|si|sgnsi=si,sgn2si=1，得到

sihi(ui(t))≤-ζi|si|.

2 數值仿真

利用龍格-庫塔法進行仿真:

當α=0.3,β=5.1,a=11,b=1.6,c=0.4,q=0.873時出現混沌吸引子，其中,

Δf1(y1,y2,y3)=cos(2πy2),

Δf2(y1,y2,y3)=0.5cos(2πy3),

Δf3(y1,y2,y3)=0.3cos(2πy2)，

hi(ui(t))=

d1(t)=0.2cos(t),d2(t)=0.6sin(t),

d3(t)=cos(3t),β+i=0.4,β-i=0.5,

βi=0.4,γi=2.5x(0)=(1,-2,-2)T,

y(0)=(1,1,-1)T,λ=1,μ=0.5.

仿真結果如圖1～3所示，從圖1可看出，不加控制器系統無法取得同步；由圖2知，加入控制器系統可快速取得同步；由圖3知，系統的誤差很快趨近于零，表明系統快速取得了同步.

圖1 無控制的主從系統狀態Fig.1 State of master-slave with no control

圖2 有控制的主從系統狀態Fig.2 State of master-slave with control

圖3 系統誤差曲線Fig.3 The system errors

3 結 論

基于穩定性理論研究了分數階多渦卷系統的有限時間同步問題，研究表明：設計非線性死區輸入的控制器以及構造適當的切換函數，能夠使主從系統取得有限時間同步，并給出了嚴格的證明.數值仿真驗證了方法的有效性.

[1]YASSENMT.Controllingchaosandsynchronizationfornewchaoticsystemusinglinearfeedbackcontrol[J]. Chaos,Solition & Fractals,2005,26(3):913-920.

[2] CHEN M, CHEN W. Robust adaptive neural network synchronization controller design for a class of time delay uncertain chaotic systems[J]. Chaos,Solition & Fractals,2009,41(5):2716-2724.

[3] PECORA L M, CAROLL T L. Synchronization in chaotic systems[J].Physics Review Letters,1990,64(8):821-824.

[4] WU X J, LU H T. Adaptive generalized function projective lag synchronization of different chaotic systems with fully uncertain parameters[J].Chaos,Solition & Fractals,2011,44(10):810-820.

[5] SALARIEH H, ALASTY A. Adaptive synchronization of two chaotic systems with with stochastic unknown parameters[J].Communications in Nonlinear Science and Numerical Simulation,2009,14(2):508-519.

[6] SUN Y P, LI J M,WANG J A,et al. Generalized projective synchronization of chaotic systems via adaptive learning control[J].Chinese Physics B,2010,19(2):502-505.

[7] YANG L, YANG J. Robust finite-time convergence of chaotic systems via adaptive terminal sliding mode scheme[J].Communications in Nonlinear Science and Numerical Simulation,2011,16(6):2405-2413.

[8] AGHABABA M P, AKBARI M E . A chattering-free robust adaptive sliding mode controller for synchronization of two different chaotic systems with unknown uncertainties and external disturbances[J].Applied Mathematics and Computation,2012,218(9):5757-5768.

[9] 孫寧，張化光，王智良.不確定分數階混沌系統的滑模投影同步[J].浙江大學學報:工學版，2010,44(7)：1288-1291. SUN N,ZHANG H G,WANG Z L.Projective synchronization of uncertain fractional order chaotic system using sliding mode controller[J].Journal of Zhejiang University:Engineering Science, 2010,44(7)：1288-1291.

[10] 余明哲,張友安.一類不確定分數階混沌系統的滑模自適應同步[J].北京航空航天大學學報，2014,40(9)：1276-1280. YU M Z ,ZHANG Y A.Sliding mode adaptive synchronization for a class of fractional-order chaotic systems with uncertainties[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(9)：1276-1280.

[11] 仲啟龍，邵永輝，鄭永愛.分數階混沌系統的主動滑模同步[J].動力學與控制學報，2015,13(1)：18-22. ZHONG Q L,SHAO Y H,ZHENG Y A.Synchronization of the fractional order chaotic systems based on TS models[J].Journal of Dynamics and Control,2015,13(1)：18-22.

[12] 孫美美，胡云安，韋建明.多渦卷超混沌系統自適應滑模同步控制[J].山東大學學報:工學版，2015，45(6):46-49. SUN M M,HU Y A,WEI J M. Synchronization of multiwing hyperchaotic systems via adaptive sliding mode control[J].Journal of Shandong University:Engineering Edition,2015，45(6):46-49.

[13] 劉恒，余海軍，向偉.帶有未知擾動的多渦卷混沌系統修正函數時滯投影同步[J].物理學報，2012,61(18)：5031-5036. LIU H, YU H J,XIANG W. Modified function projective lag synchronization for multi-scroll chaotic system with unknown disturbances[J].Acta Phys Sin,2012,61(18):5031-5036.

[14] 毛北行，王戰偉.一類分數階復雜網絡系統的有限時間同步控制[J].深圳大學學報:理工版，2016,33(1)：96-101.

MAO B X，WANG Z W. Finite-time synchronization of a class of fractional-order complex network systems[J].Journal of Shenzhen University:Science and Engineering,2016,33(1)：96-101.

[15] 田小敏，費樹岷，柴琳.具有死區輸入的分數階混沌系統的有限時間同步[J].控制理論與應用，2015,32(9)：1240-1245. TIAN X M，FEI S M，CHAI L. Finite-time synchronization of chaotic systems by considering dead-zone phenomenon[J].Control Theory and Applications,2015,32(9)：1240-1245.

[16] PODLUBNY. Fractional Differential Equation[M] .New York: Academic Press,1999.

[17] BHAT S P, BERNSTEIN D S. Geometric homogeneity with applications to finite-time stability[J]. Mathematics of Control Signals and Systems,2005,17(2):101-127.

[18] MOHAMMAD P A, SOHRAB K, GHASSEM A. Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique[J]. Applied Mathematical Modelling,2011,35(6):3080-3091.

Finite-time synchronization of fractional-order multi-scroll systems with dead-zone input.

MAO Beixing, MENG Xiaoling

(CollegeofScience,ZhengzhouUniversityofAeronautics,Zhengzhou450015,China)

The problem of finite-time synchronization of fractional-order multi-scroll systems with dead-zone input is studied. The sufficient conditions for the fractional order systems to get finite-time synchronization are obtained based on fractional order calculus theory. The research conclusion illustrates that fractional-order multi-scroll systems is finite-time chaos synchronization under proper conditions.

fractional order; multi-scroll systems; sliding model; chaos synchronization

2016-07-26.

國家自然科學基金資助項目(NSFC1501525).

毛北行(1976-)，ORCID：http:∥orcid.org/0000-0002-9232-3434，男，碩士，副教授，主要從事分數階混沌系統研究，E-mail：bxmao329@163.com.

10.3785/j.issn.1008-9497.2017.03.010

O 231

A

1008-9497(2017)03-302-05