隨機波動模型的首中時問題

張苗，劉暉，張飛龍

(1.西安電子科技大學 數學與統計學院， 陜西 西安 710126； 2. 北京大學 地球與空間科學學院，北京 100871； 3. 西安電子科技大學 物理與光電工程學院， 陜西 西安 710126)

隨機波動模型的首中時問題

張苗1，劉暉2，張飛龍3

(1.西安電子科技大學 數學與統計學院， 陜西 西安 710126； 2. 北京大學 地球與空間科學學院，北京 100871； 3. 西安電子科技大學 物理與光電工程學院， 陜西 西安 710126)

研究了一類波動率是平方根過程的隨機波動CEV模型的首中時問題.利用鞅方法求解首中時和波動率的聯合拉普拉斯變換，繼而將問題轉換為求解一類變系數二階常微分方程，通過變量代換將此方程轉化為經典的Whittaker方程，得到聯合拉普拉斯變換表達式.最后，選取不同的參數，使隨機波動CEV模型的資產價格過程能夠涵蓋O-U過程、幾何布朗運動、平方根過程等幾種常見的擴散過程，畫出不同參數下聯合拉普拉斯變換函數的三維圖像，并分析其變化趨勢.

隨機波動CEV模型;首中時;鞅方法;聯合拉普拉斯變換;Whittaker方程

Journal of Zhejiang University(Science Edition), 2017,44(3):296-301

為了有效規避期權市場風險，BLACK等[1]提出了Black-Scholes期權定價模型(也稱B-S模型).經典的B-S模型建立在波動率為常數這一假設基礎之上，然而，大量研究表明，隱含波動率常呈現“微笑”的特征，這與B-S模型的基本假設相矛盾.為此，提出了隨機波動模型[2-4].本文討論的隨機波動CEV(亦稱常彈性方差)模型也是隨機波動模型的一種，可用2個擴散方程描述，即資產價格過程和波動過程[5]，其中波動過程是平方根擴散過程，資產價格過程則涵蓋了Ornstein-Uhlenbec過程(也稱O-U過程)、幾何布朗運動、平方根過程等幾種常見的擴散過程.

近年來，首中時問題被廣泛研究，MARIO[6]總結和推廣了CARLSUND[7]的結論，得到布朗運動首中時的生成函數.文獻[8-11]對O-U過程和反射O-U過程的首中時問題進行了研究.同時，文獻[12]討論了反射CEV模型的首中時問題，利用鞅方法計算得到首中時的拉普拉斯變換.以上研究均只針對單變量擴散過程，對隨機波動CEV模型的雙變量擴散過程首中時的研究卻非常少.

本文借鑒單變量擴散過程首中時問題的求解方法——鞅方法[13-16]，在βcY+α=0這一假定條件下，將隨機波動模型的首中時問題轉化為求解一類變系數二階常微分方程，通過變量代換[17-19]，將此方程轉化為Whittaker方程，最終計算首中時和波動率的聯合拉普拉斯變換.

1 隨機波動CEV模型

盡管B-S期權定價模型的改進方法眾多，但因隨機波動模型獨具優勢，能夠很好地描述時變波動，被廣泛應用于建模利率期限結構和期權定價研究.

通常，隨機波動模型描述成如下隨機微分方程：

(1)

其中，Y=(Yt;t≥0)為隨機波動因子，滿足:

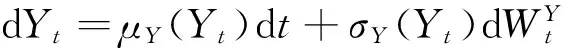
在常方差彈性過程中，方程(2)應為：

(3)

其中，φ(x)=aYxν，0≤ν≤1，系數aY為波動率的波動，ν為方差彈性.當ν=0.5時，為HESTON提出的均值回歸過程；當ν=1時，為GARCH擴散過程.

本文主要考慮如下形式的隨機波動CEV模型：

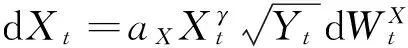
(4)

其中，γ≥0,aX>0,cY>0,bY≥0,aY>0.

2 首中時和隨機波動因子的聯合拉普拉斯變換

本節的目標是得到隨機變量(Yτl,τl)的聯合拉普拉斯變換表達式.對一個已知的首中閥值l∈R，定義隨機波動模型的首中時如下：

τl=inf(t≥0;Xτl=l),

(5)

特別地，取infφ=∞.

通常情況下，由于很難得到隨機變量(Yτl,τl)的聯合分布表達式，因此可用聯合拉普拉斯變換來代替.隨機變量(Yτl,τl)的聯合拉普拉斯變換定義如下：

φ(l;x,y)=Ex,y[exp(-ατl-βYτl)],

(6)

其中，E是期望算子且

Ex,y[·]=E[·|X0=x,Y0=y].

定理1 設非零函數f∈C2(R2)，R為實數，滿足方程：

(7)

(8)

證明 用鞅方法求解式(6)的解析表達式.首先，對f(x)∈C2(R2)應用It公式，得

定義：

那么M=(Mt;t≥0)是一個局部鞅.由分部積分公式，得：

因為函數f(x)滿足方程(7)，并且βcY+α=0，則有

ρaXaYβxγf′(x)y-αf(x)=

這樣

注意到Xτl=l，P-a.s.，于是令t→∞，

Ex,y[e-ατl-βYτlf(l)]=e-βyf(x).

可以證明

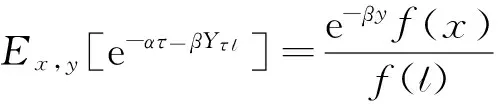
此時，只要知道方程(7)的通解f(x)，就可以得到隨機變量(Yτl,τl)對應的聯合拉普拉斯變換，因此，本文接下來的工作重點就是求解方程(7).

用變量代換法求解常微分方程(7).

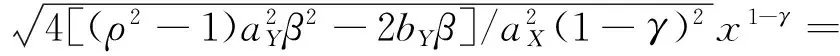
因為

代入方程(7)得

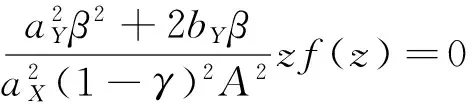
(9)

其中，

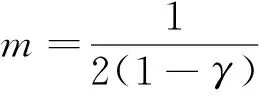
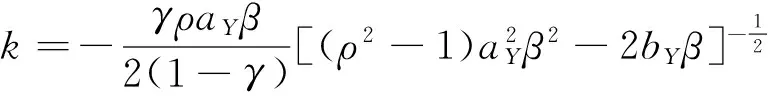
情況2γ=1，此時常微分方程(7)是歐拉方程，其通解為

f(x)=C1xλ1+C2xλ2,

其中λ1和λ2是常微分方程(7)的2個不相等的特征值.

將求出的通解f(x)代入定理1的式(8)，即有：

定理2 令(x,y)∈R×R+，R為實數，對滿足條件βcY+α=0的(α,β)，隨機變量(Yτl,τl)對應的聯合拉普拉斯變換為

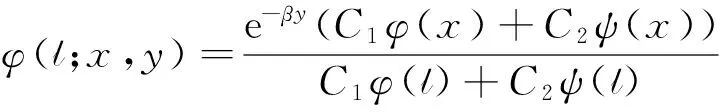
(10)

其中超幾何函數φ(x)和ψ(x)定義為

同時，

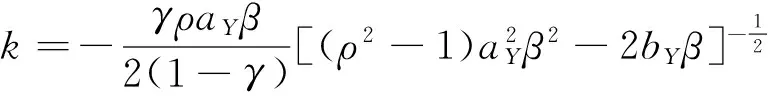
3 推論和結果分析

推論1 當γ=0時，令(x,y)∈R×R+，對任意滿足條件βcY+α=0的(α,β)，隨機變量(Yτl,τl)對應的聯合拉普拉斯變換為

φ(l;x,y)=

其中,

φ(l;x,y)=

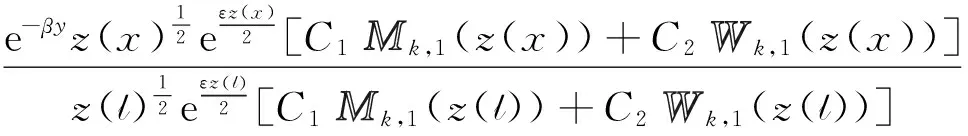
其中,

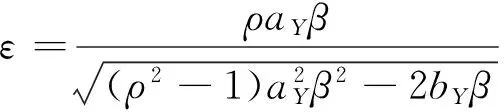
推論3 當γ=1，令(x,y)∈R×R+，對任意滿足條件βcY+α=0的(α,β)，隨機變量(Yτl,τl)對應的聯合拉普拉斯變換為

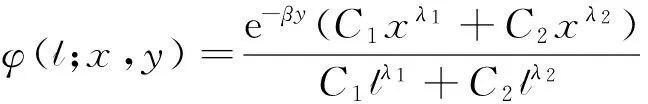
其中，λ1和λ2是常微分方程(7)的2個不相等的特征值.

利用這3個推論，分別畫出當資產價格過程是O-U過程、平方根過程以及幾何布朗運動時，聯合拉普拉斯變化函數(x,y)→φ(l;x,y)的圖像，并分析其變化趨勢.

這里，取系數aX=1,aY=1,β=0.5以及首中閥值l=1，首先畫出當γ=0，ρ分別取-1，0，0.5和1時，聯合拉普拉斯變化函數(x,y)→φ(l;x,y).

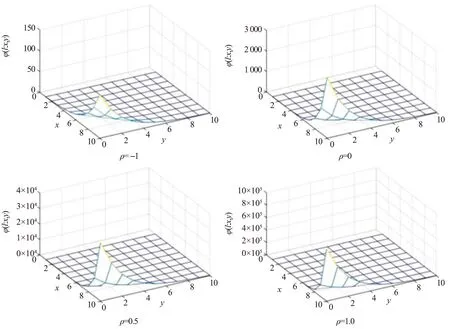
圖1 當γ=0，聯合拉普拉斯變化函數(x,y)→φ(l;x,y)Fig.1 The joint Laplace transform function (x,y)→φ(l;x,y) when γ=0

從圖1可看出相關程度ρ和(Xt,Yt)初值(x,y)的選取對φ值的影響.首先，在不同相關程度ρ下，x取值越大，y取值越小,φ值就越大.隨著相關程度的降低，φ值整體呈下降趨勢.并且在不同相關程度ρ下，函數(x,y)→φ(l;x,y)的整體變化趨勢基本相同.

圖2 當，聯合拉普拉斯變化函數(x,y)→φ(l;x,y)Fig.

圖3 當γ=1，聯合拉普拉斯變化函數(x,y)→φ(l;x,y)Fig.3 The joint Laplace transform function (x,y)→φ(l;x,y) when γ=1

4 結 論

研究了一類波動率是平方根過程的隨機波動CEV模型的首中時問題.利用鞅方法求解得到首中時和波動率的聯合拉普拉斯變換表達式，并分析函數(x,y)→φ(l;x,y)在不同參數下的變化趨勢.不足之處是，在給出拉普拉斯變換的顯式表達式時，需有限定條件βcY+α=0.去除或弱化這一條件，使求解的拉普拉斯變換更為嚴格，這一問題有待進一步研究.

[1]BLACKF,SCHOLEM.Thepricingofoptionsandcorporateliabilities[J]. Journal of Political Economy,1973,81(3):133-155.

[2] HESTON S L. A closed-form solution for options with stochastic volatility with applications to bond and currency options[J]. The Review of Financial Studies,1993,6(2):327-343.

[3] HULL J,WHITE A. The pricing of options on assets with Stochastic volatility[J].Journal of Finance,1987,42(2):281-300.

[4] STEIN E, STEIN C. Stock price distributions with stochastic volatility: An analytic approach[J].Review of Financial Studies,1991(4):727-752.

[5] TALAMANCA G F. Testing volatility autocorrelation in the constant elasticity of variance stochastic volatility model[J]. Computational Statistics and Data Analysis,2009,53:2201-2218.

[6] MARIO L. First passage problems for asymmetric wiener processes[J]. Ecolepoly Technique de Montreal,2006,43(4):175-184.

[7] CARLSUND A. Cover Times, Sign-Dependent Random Walks, and Maxima[M]. Stockholm： Matematik,2003.

[8] BOROVKOV K, NOVIKOV A. On exit times of Levy-driven Ornstein-Uhlenbeck processes[J]. Statistics & Probability Letters,2007,78(12):1517-1525.

[9] PATIE P. On a martingale associated to generalized Ornstein-Uhlenbeck processes and an application to finance[J]. Stoch Process，2005,115:593-607.

[10] LOEFFEN R L, PATIE P. Absolute ruin in the Ornstein-Uhlenbeck type risk model[J]. Quantitative Finance,2010,arXiv:1006.2712.

[11] ALILI L, PATIE P, PEDERSEN J L. Representations of the first hitting time density of an Ornstein-Uhlenbeck process[J]. Stock Models,2005,21:967-980.

[12] BO L J, HAO C. First passage times of constant-elasticity-of-variance processes with two-sided reflecting barriers[J]. Journal of Applied Probability,2012,49(4):1119-1133.

[13] GERBER H U, YANG H L. Absolute ruin probabilities in a jump diffusion risk model with investment[J]. NAAJ,2007,1l(3):159-168.

[14] BO L J, REN G, WANG Y J. First passage times of reflected generalized Ornstein-Uhlenbeck processes [J]. Stochastics and Dynamics,2013,13(1):1250014.

[15] BO L J, WANG Y J. Some integral functionals of reflected SDEs and their applications in finance[J]. Quantitative Finance,2011,11(11):343-348.

[16] BO L J, TANG D, WANG Y J, et al. On the conditional default probability in a regulated market: A structural approach[J]. Quantitative Finance,2010,11(12):1695-1702.

[17] 馮海林，薄立軍.隨機過程——計算與應用[M].西安：西安電子科技大學出版社，2012. FENG H L，BO L J. Stochastic Process—Calculation and Application[M]. Xi’an:Xidian University Press,2012.

[18] 孫健.金融衍生品定價模型—數理金融引論[M].北京：中國經濟出版社，2008. SUN J. Financial Derivatives Pricing Model-An Introduction to Mathematical Finance[M]. Beijing: China Economy Press,2008.

[19] 王高雄，周之銘.常微分方程[M].北京：高等教育出版社，2006. WANG G X, ZHOU Z M. Ordinary Differential Equations[M]. Beijing: Higher Education Press,2006.

The first hitting time of stochastic volatility models.

ZHANG Miao1, LIU Hui2, ZHANG Feilong3

(1.SchoolofMathematicsandStatistics,XidianUniversity,Xi’an710126,China； 2.SchoolofEarthandSpaceScienecs,PekingUniversity,Beijing100871,China； 3.SchoolofPhysicsandOptoelectronicEngineering,XidianUniversity,Xi’an710126,China)

This paper explores the first passage times of stochastic volatility CEV model. We mainly solve the joint Laplace transform of the first hitting time and volatility. Firstly, we use the Itformula to construct the martingale which can convert the problem into the process of solving a differential equation. Then, we introduce an appropriate second order variable coefficient ordinary differential equation, after a change of variable, it is turned to the Whittaker's equation. It’s not difficult to get the general solution of Whittaker’s equation. Thus, the explicit expressions for the joint Laplace transformation of the first passage times of stochastic volatility CEV model can be derived. Finally, selecting the parametersγbe 0, 1/2 and 1, let the asset price process covers the O-U process, geometric Brownian motion and square root process. Under different parameters, we obtain explicit expression of the joint Laplace transformation function, and use Matlab to draw the corresponding diagram and analyze the trend of graph.

stochastic volatility CEV model; first passage times; martingale method; joint Laplace transforms; Whittaker’s equation

2016-07-16.

國家自然科學基金資助項目(11471254).

張苗(1993-)，ORCID：http://orcid.org/0000-0003-1640-3173，女，碩士研究生，主要從事隨機模型研究，E-mail：feilon1001@163.com.

10.3785/j.issn.1008-9497.2017.03.009

O 211.63

A

1008-9497(2017)03-296-06