一類分數階非線性微分包含初值問題的可解性

楊小娟, 韓曉玲

(西北師范大學 數學與統計學院, 甘肅 蘭州, 730070)

一類分數階非線性微分包含初值問題的可解性

楊小娟, 韓曉玲*

(西北師范大學 數學與統計學院, 甘肅 蘭州, 730070)

微分包含; 分數階導數; 可解性;Bohnenblust-Karlin不動點定理

JournalofZhejiangUniversity(ScienceEdition), 2017,44(3):287-291

0 引 言

微分包含是微分方程與集值分析的交叉學科,在力學、工程學以及優化與控制理論中有著廣泛的應用[1-2].在描述物理、力學、工程、微觀經濟學等系統時一般都用確定的微分方程模型,但在實際生活及科學實踐中,確定的模型通常不適合描述某些動態系統.例如,通常假定微分方程x′(t)=f(t,x(t))的右端為連續函數,但實際中往往難以保證,若將f(t,x(t))嵌入到集值映射F(t,x(t))中,可將其轉化為研究微分包含x′(t)∈F(t,x(t)).如文獻[2]研究了一階微分包含周期邊值問題

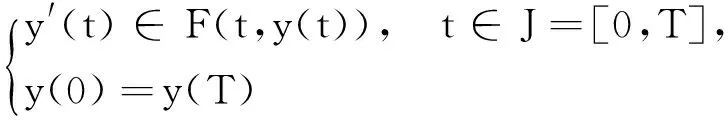
的可解性.

分數階微分方程被廣泛應用于解決各領域的工程問題,如光學、流變學、新材料力學系統等[3-5].此外,在生物學、最優控制等領域亦通過建立微分包含模型對一些實際問題進行理論分析和研究.分數階微分包含越來越受國內外學者的關注,并取得了一些很好的成果[6].文獻[7]介紹了一種新的局部分數階導數的定義,稱為一致分數階導數,較Riemann-Liouville和Caputo這2種分數階導數具有更好的性質.文獻[8]證明了一致分數階導數的鏈式法則、Gronwall不等式以及Laplace變換.文獻[9]給出了分數階導數的一些有意義的計算方法.文獻[10]通過定義一個tube解并運用Schauder不動點定理研究了分數階Cauchy問題

的可解性.

受以上研究的啟發,在新的一致分數階導數的定義下,運用集值映射的不動點定理研究了微分包含問題

(1)

的可解性，并通過定義問題(1)的上下解得到了該問題解的最佳逼近.

1 預備知識

記J=[a,b],C(J)為定義在J上的連續實值函數構成的Banach空間,其范數為‖x‖∞=sup{|x(t)|t∈J}.設Ck(J)為k次連續可微實值函數構成的Banach空間,其范數為‖x‖ck=max{‖x‖∞,…,‖x(k)‖∞}.設L1(J,R)為定義在J上滿足∫J|x(t)|dt<+∞可測函數構成的Banach空間,其范數為‖x‖L1=∫J|x(t)|dt.設AC(X)表示X的絕對連續函數全體,CC(X)表示X的非空凸的緊子集全體,BCC(X)表示X的有界非空凸的緊子集全體.

設(X,|·|)是Banach空間,若對任意的x∈X,G(x)是凸(閉)值的,則集值映射G:X→2R是凸(閉)值的.

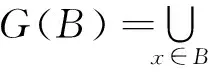
設對任意的x0∈X,G(x0)是X的非空閉子集,且對每個包含G(x0)的N?X,存在x0的開鄰域M使得G(M)?N,則稱G是上半連續的;設B?X為有界集,若G(B)是相對緊的,則稱G是全連續的;設集值映射G是非空緊的全連續映射,則G是上半連續的充要條件是G有閉圖像(即xn→x*,hn→h*,hn→G(xn)?h*→G(x*)).

若存在x∈X使得x∈G(x),則G有一個不動點.

以下是一致分數階導數和微分包含的一些相關結論,詳見文獻[6-9,11-15].

定義1(一致分數階導數) 設α∈(0,1]且f:[0,∞)→R,f的一致分數階導數可定義為

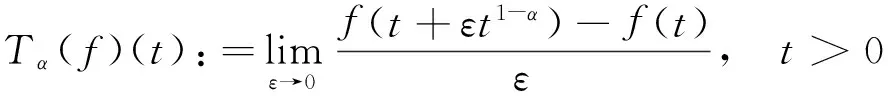
常用fα表示.如果Tα(f)存在,則定義

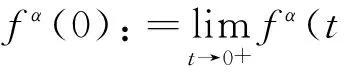
定義2(一致分數次積分) 設α∈(0,1]且f:[0,∞)→R，f在[a,t]上的α次分數積分可定義為

命題3 設r∈Cα([a,b],R),00}上有rα(t)<0.若r(a)≤0,則對任意t∈[a,b],有r(t)≤0.

定義3 集值映射F:J×R→2R若滿足：

(i)對任意的x∈R,有t→F(t,x)是可測的；

(ii)對幾乎處處的t∈J,有x→F(t,x)是上半連續的；

(iii)對任意的k>0,存在hk∈L1(J,R+),使得‖F(t,x)‖=sup{|v|:v∈F(t,x)}≤hk(t),其中|x|≤k,t∈J；

則其是L1-Carathéodary函數.

引理2[12]設I是緊的實區間，且X是Banach空間,令F:I×X→CC(X).對任意的y∈X,(t,x)→F(t,x)關于t可測,且對幾乎處處的t∈I,(t,x)→F(t,x)關于x是上半連續的.對于每個不動點x∈C[J,R],定義SF,x={v∈L1(J,R):v(t)∈F(t,x(t)),t∈J}≠?,且設Γ:L1(I,X)→C(I,X)是線性連續映射,則算子Γ°SF:C(I,X)→CC(I,X),x→(Γ°SF)(x):=Γ(SF,x)是C(I,X)×C(I,X)的閉圖像算子.

引理3[16]若g∈L1(J,R),則函數x:J→R,

(2)

的解.

定義4 函數x∈AC(J,R)是式(1)的解,如果存在v∈F(t,x(t)),對任意的t∈J,使得xα(t)=v(t)且x(a)=x0.

2 主要結果及其證明

定義5 設φ∈AC(J,R),若存在v1∈L1(J,R)，滿足

則稱φ(t)是式(1)的下解.

定義6 設ψ∈AC(J,R)，若存在v2∈L1(J,R),滿足

則稱ψ(t)是式(1)的上解.

定理1 設F:J×R→CC(R)是L1-Carathéodary集值映射,若存在φ,ψ∈AC(J,R),分別是式(1)的下解與上解,其中φ≤ψ.令E={(t,x)∈J×R|φ(t)≤x(t)≤ψ(t)},則對任意的t∈J,式(1)至少有1個解x∈E滿足φ(t)≤x(t)≤ψ(t).

(3)

其中，γ:J×R→R定義為

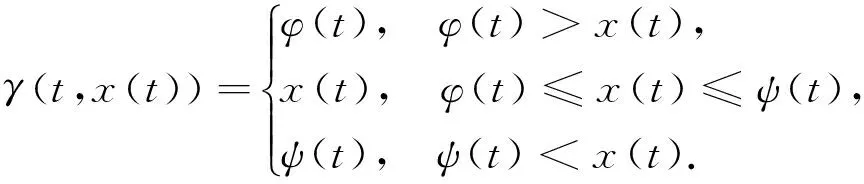
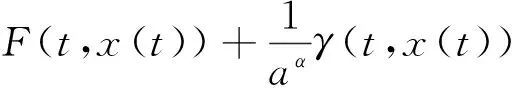
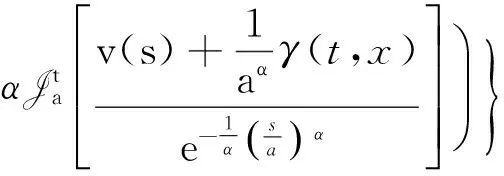
只需證明算子T滿足引理1的假設條件,從而可得T有不動點即式(2)的解.

下面分兩部分證明：

第1部分:證明上述定義的算子T有不動點.

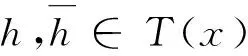
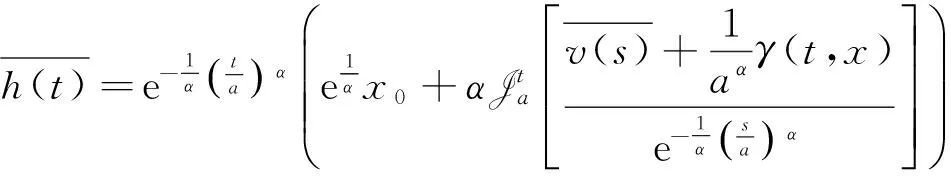
設0≤λ≤1,則對每一個t∈J,有

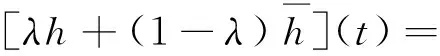
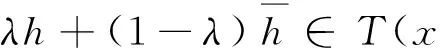
ii)對任意常數r>0,令Br={x∈C(J):‖x‖≤r},則Br為C(J)上的有界閉凸集.下證存在r>0,使得T(Br)?Br.

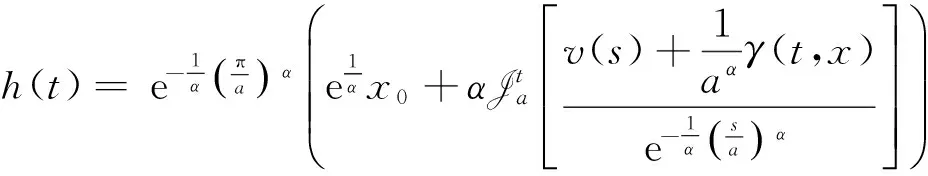
對任意的t∈J,有

|hr(t)|=

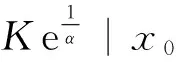
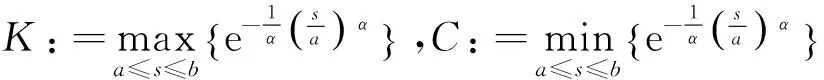
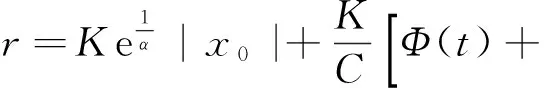
則‖hr‖≤r,即存在r>0,使得T(Br)?Br.

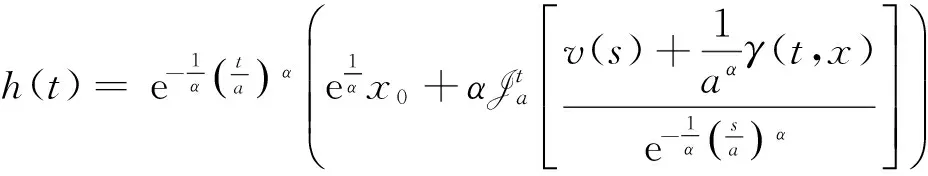
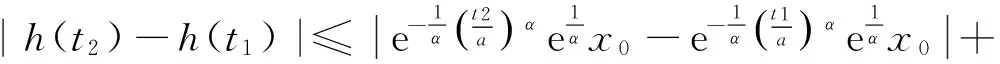
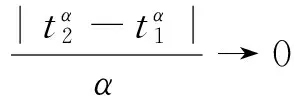
由i)～iii)知T是緊值映射.

iv)T有閉圖像.設xn→x*,hn∈T(xn),且hn→h*,下證h*∈T(x*).

由hn∈T(xn)可知，存在vn∈SF,xn,使得

需證存在v*∈SF,x*,使得對任意的t∈J,

因為xn→x*,hn→h*,且r連續,則當n→∞時,

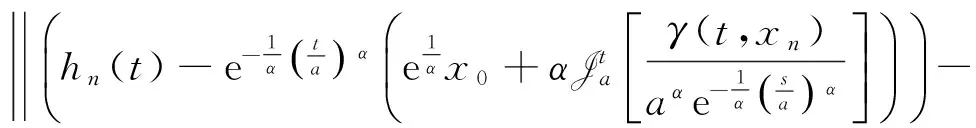
考慮線性連續算子Γ:L1(J,R)→C(J,R),

命題4 Γ°SF是閉圖像算子,而且有

Γ(SF,xn).

因為yn→y*,由命題1知,對某些v*∈SF,x*,有

結合i)～iv),T滿足命題3的假設,從而T有不動點，即式(3)的解.

第2部分:證明式(3)的任意解x(t)：φ(t)≤x(t)≤ψ(t).

hα(t0)=(φ(t0)-x(t0))α=φα(t0)-xα(t0)≤v1(t)-v(t)≤0，

且h(a)=φ(a)-x(a)≤x0-x0=0,即h(a)≤0,由命題3,任意t∈J,h(t)≤0,與h(t)>0矛盾,從而φ(t)≤x(t),t∈J.

同理可證x(t)≤ψ(t).

綜上可得,式(3)至少有1個解x∈ACα(J,R),使得對任意t∈J,有φ(t)≤x(t)≤ψ(t),而此時γ(t,x(t))=x(t),式(3)即為式(1),定理得證.

推論1(次線性增長條件) 假設F:J×R→BCC(R),(t,x)→F(t,x)關于t可測、關于x上半連續,且存在函數a(t),b(t)∈L1(J,R+),μ∈[0,1],使得

‖F(t,x)‖≤a(t)|x|μ+b(t), (t,x)∈J×R,

則式(1)至少有1個解.

證明 在該假設條件下,取hk(t)=a(t)|x|μ+b(t),由定理1即可證得.

推論2(至多線性增長條件) 假設F:J×R→BCC(R),(t,x)→F(t,x)關于t可測、關于x上半連續,且存在函數a(t),b(t)∈L1(J,R+),使得

‖F(t,x)‖≤a(t)|x|+b(t), (t,x)∈J×R，

則式(1)至少有1個解.

證明 在該假設條件下,取hk(t)=a(t)|x|+b(t),由定理1即可證得.

[1]ABBASBANDYS,NIETOJJ,ALAVIM.Tuningofreachablesetinonedimensionalfuzzydifferentialinclusions[J]. Chaos Solitons Fractals,2005,26:1337-1341.

[2] BENCHONRA M, NTOUYAS S K. On first order differential inclusions with periodic boundary conditions[J]. Math Inequal Appl,2005,8(1):71-78.

[3] LAKSHMIKANTHAM V, VATSALA A S. Basic theory of fractional differential equations[J]. Nonlinear Analysis，2008,69(18):2677-2682.

[4] HENDERSON J, OUAHAB A. Fractional functional differential inclusions with finite delay[J]. Nonlinear Analysis,2009,70(5):2091-2105.

[5] BENCHOHRA M, HENDERSON J, NTOUYAS S K, et al. Existence results for fractional functional differential inclusions with infinite delay and application to control theory[J]. Fractional Calculus and Applied Analysis，2008,11(1):35-36.

[6] CHENG Y, ZHU G, MARICHEV O I. Existence of solutions to fractional differential equations[J]. Bull Math Anal Appl，2015,310(1):26-29.

[7] KHALIL R, AI HORANI M, YOUSEF A, et al. A new definition of fractional derivative[J]. J Comput Appl Math，2014,264:65-70.

[8] CHANG Y K, NIETO J J. Some new existence results for fractional differential inclusions with boundary conditions[J]. Math Comput Modelling，2009,49:605-609.

[9] SAMKO S G, KIBAS A A，MARICHEV O I. Fractional Integrals and Derivatives:Theory and Applications[M]. Yverdon: Gordon and Breach Science Publisher，1993.

[10] BOHNENBLUST H F, KARLIN S. On a Theorem of Ville, Contributions to Theory of Games[M]. Princeton: Princeton University Press,1950(1):155-160.

[11] CHUNG W S. Fractional Newton mechanics with conformable fractional derivative[J]. J Comput Appl Math,2015,290:150-158.

[12] LASOTA A, OPIAL Z. An application of the Kakutani-Ky Fan theorem in the theory of ordinary differential equations[J]. Bull Acad Pol Sci Ser Sci Math Astronom Phys，1965(13):781-786.

[13] CHANG Y K, LI W T, NIETO J J. Controllability of evolution differential inclusions in Banach spaces[J]. Nonlinear Anal TMA，2007,67:623-632.

[14] KATUGAMPOLA U N. A new fractional derivative with classical properties[J/OL].Journal of the American Mathematical Society. [2015-03-19].http:∥www.researchgate.net/publication/267395593.

[15] FENG Y Q, TONG P. Existence and nonexistence of positive periodic solutions to a differential inclusion[J]. Topological Methods in Nonlinear Analysis,2013,42:449-459.

[16] BAYOUR B, TORRES D F M. Existence of solution to a local fractional nonlinear differential equation[J]. J Comput Appl Math，2016,312:127-133.

ThesolvabilityofCauchyproblemfornonlinearfractionaldifferentialinclusions.

YANGXiaojuan,HANXiaoling

(College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China)

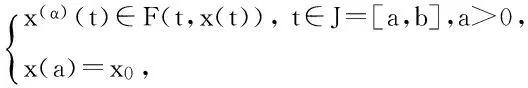
differentialinclusions;fractionlderivatives;existenceofsolutions;Bohnenblust-Karlin’sfixedpointtheorem

2016-05-25.

國家自然科學基金資助項目(11561063).

楊小娟 (1992-), ORCID:http:∥orcid.org/0000-0002-7738-9021，女, 碩士研究生, 主要從事常微分方程邊值問題研究，E-mail:18394172453@163.com.

*通信作者， ORCID： http:∥orcid.org/0000-0002-0670-9657, E-mail: hanxiaoling9@163.com.

10.3785/j.issn.1008-9497.2017.03.007

O

A

1008-9497(2017)03-287-05