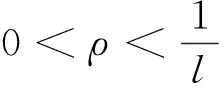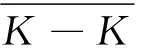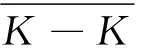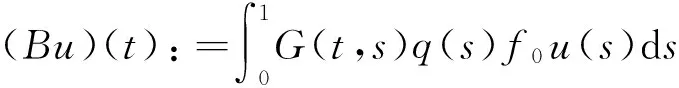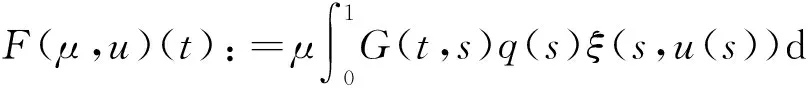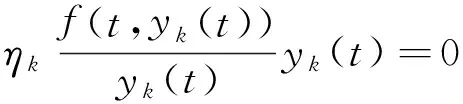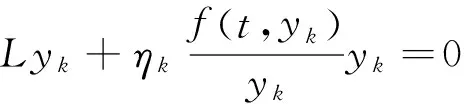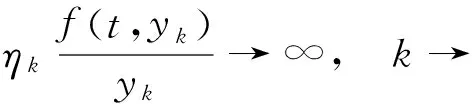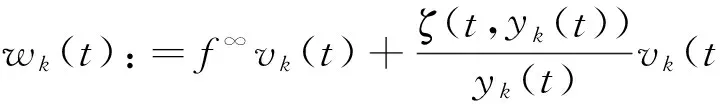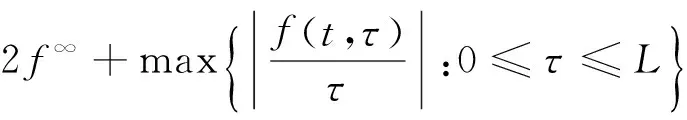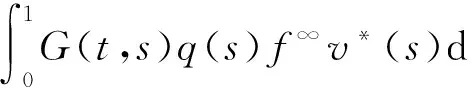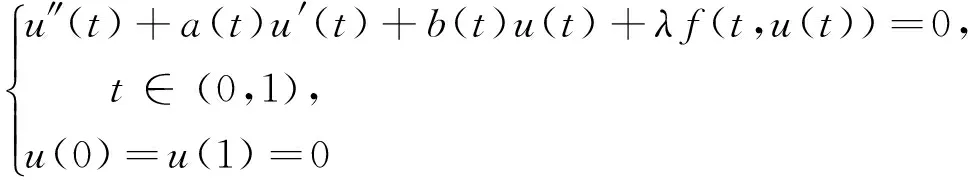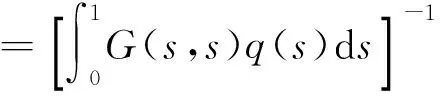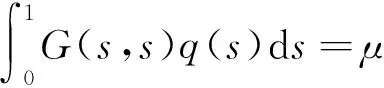一類奇異邊值問題正解的存在性及多解性

閆東明

(浙江財經大學 數據科學學院， 浙江 杭州 310018)

一類奇異邊值問題正解的存在性及多解性

閆東明

(浙江財經大學 數據科學學院， 浙江 杭州 310018)

奇異邊值問題;全局分歧;正解;多解性;第1特征值

JournalofZhejiangUniversity(ScienceEdition), 2017,44(3):281-286，328

0 引 言

奇異邊值問題因其具有的物理意義引起了人們的廣泛關注,并且此類問題的相關研究也取得了許多深刻的結果[1-8].同時，鑒于正解及多個正解的實際意義,奇異邊值問題正解及多個正解存在性的研究顯得更為活躍.文獻[6]研究了奇異邊值問題

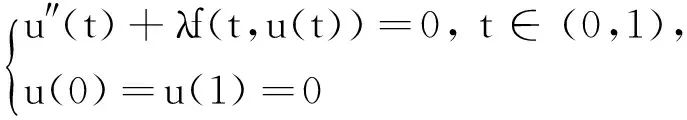
(1)

正解的存在性.在非線性項f滿足非負性及一些局部增長性條件下,獲得了奇異邊值問題(1)的一個正解的存在性結果,并給出了問題(1)有正解存在和無正解存在時非負參數λ的取值范圍.文獻[8]研究了帶一般微分算子的奇異邊值問題：

(2)多個正解的存在性.通過構造奇異邊值問題(2)的格林函數,并運用Leggett-Williams不動點定理,在非線性項f滿足非負性條件及一些局部條件下,獲得了奇異邊值問題(2)多個正解的存在性結果.

另外,文獻[9-10]運用Rabinowitz全局分歧理論以及區間分歧方法，對Dirichlet邊值問題正解集的結構和全局分歧進行了討論,獲得了大量有價值的結果.

上述文獻從不同的角度豐富了常微分方程奇異邊值問題正解的存在性理論.然而,這些研究所得到的奇異邊值問題有正解及多個正解存在的充分性條件中所涉及的數值均非最優,且所得充分性條件與奇異邊值問題對應的線性問題的第1個特征值之間沒有建立聯系，而邊值問題對應的線性問題的特征值在邊值問題正解及多個正解存在性的研究中是一個很本質的量.本文運用Dancer全局分歧定理[11]對二階常微分方程奇異邊值問題(2)進行研究，試圖給出此類問題有正解存在且與其相應線性問題第1個特征值有關的充分條件,以及說明這些充分條件中所涉及的值是最優的.無論是方法還是所得結果,本研究都將進一步豐富二階常微分方程奇異邊值問題正解的存在性理論.

本文總假定

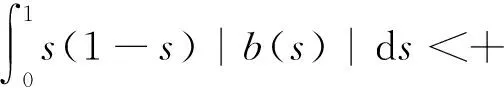
(A2)f:[0,1]×[0,+∞)→[0,+∞)連續.

1 預備知識及引理

記C[0,1]為定義在[0,1]上的連續實值函數構成的集合,定義范數

‖x‖∞=sup{|x(t)||t∈[0,1]},

則C[0,1]為Banach空間.記[0,1]上的所有絕對連續函數全體為AC[0,1].令

ACloc[0,1)={u|u|[0,d]∈AC[0,d],[0,d]?[0,1)},

ACloc(0,1]={u|u|[d,1]∈AC[d,1],[d,1]?(0,1]}，

方便起見，記

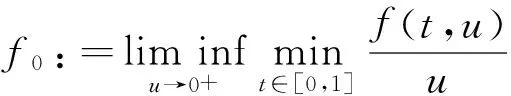
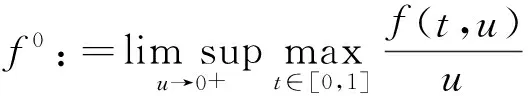
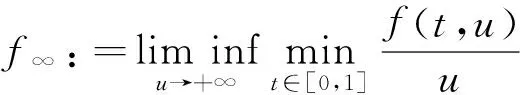
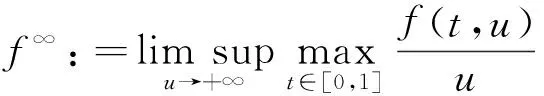
引理1[8]假設(A1)成立.則

(i)初值問題

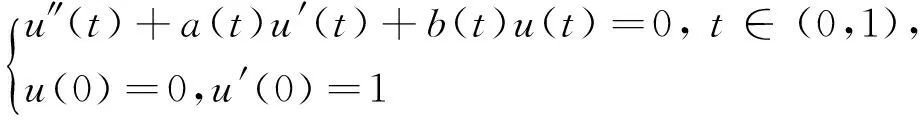
有唯一解α∈AC[0,1]∩C1[0,1)且α′∈ACloc[0,1);

(ii)初值問題

有唯一解β∈AC[0,1]∩C1(0,1]且β′∈ACloc(0,1];

(iii)α在[0,1]非減,β在[0,1]非增.

設

引理2 設(A1)成立.則G具有以下性質:

(i)G(t,s)>0, (t,s)∈(0,1)×(0,1);

(ii)G(t,s)≤G(t,t), (t,s)∈[0,1]×[0,1];

(iii)G(t,s)≥δt(1-t)G(s,s), (t,s)∈[0,1]×[0,1],其中δ>0為常數.

證明 由引理1易證(i)、(ii).以下證(iii)成立.

(3)

(4)

由G的定義、引理1以及式(3)和(4)，有

即

G(t,s)≥δt(1-t)G(s,s), (t,s)∈[0,1]×[0,1],

定義P={u∈C[0,1]:u(t)≥0,t∈[0,1],u(0)=u(1)=0}.則P是C[0,1]中的一個錐.設

(5)

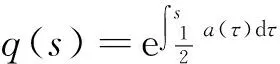
根據Krein-Rutmann定理[11-12],有下述引理.

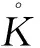
令Eu0={u|u∈C[0,1]且存在λ>0使得

-λt(1-t)≤u(t)≤λt(1-t),t∈[0,1]}.

若u∈Eu0,則令u的范數為

‖u‖u0= inf{λ|λ>0,-λt(1-t)≤

u(t)≤λt(1-t),t∈[0,1]}.

(6)

此處‖u‖u0為u的u0-范數,相關內容可參見文獻[14].

引理4 (Eu0,‖·‖u0)是Banach空間.

證明 設{un}是(Eu0,‖·‖u0)中的Cauchy列.則有

‖un-um‖→0,n,m→∞.

(7)

由式(6)和(7),對?ε>0，存在N>0使得

-εt(1-t)≤un(t)-um(t)≤εt(1-t),

t∈[0,1], ?n,m>N.

(8)

從而,

即{un}是(C[0,1],‖·‖∞)中的Cauchy列.根據(C[0,1],‖·‖∞)的完備性,存在u0∈C[0,1]使得

‖un-u0‖∞→0,n→∞.

在式(8)中令m→∞，則有

-εt(1-t)≤un(t)-u0(t)≤εt(1-t),

t∈[0,1],(n>N),

即

‖un-u0‖u0≤ε,n>N.

因此,對Cauchy列{un}?(Eu0,‖·‖u0),存在u0∈Eu0使得

‖un-u0‖u0→0,n→∞.

所以,(Eu0,‖·‖u0)是Banach空間.引理證畢.

引理5 設(A1)成立,算子T如式(5)所定義.則T的譜半徑r(T)>0,且T有一個正的特征函數φ1對應于其第1個特征值λ1=(r(T))-1,即φ1=λ1Tφ1.

下證T是一個強正算子.設u∈K{θ}.則u在[0,1]上不恒為0,并且由K的定義知,存在λ0>0,使得

0≤u(t)≤λ0t(1-t),t∈[0,1].

(9)

由引理1以及式(3)、(4)和(9)，有

c2u[t(1-t)],t∈[0,1]

和

c1u[t(1-t)],t∈[0,1],

其中,

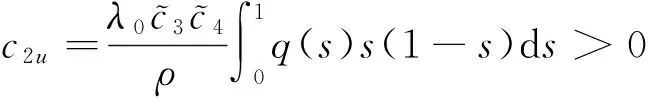
ρ,δ見引理2.從而,對u∈K{θ}存在常數c1u,c2u>0,使得

c1u[t(1-t)]≤(Tu)(t)≤c2u[t(1-t)],t∈[0,1],

即

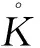
所以T是一個強正算子.

由引理3可知,T的譜半徑r(T)≠0,且T有一個正的特征函數φ1對應于其第1個特征值λ1=(r(T))-1,并且滿足φ1=λ1Tφ1.引理證畢.

注1 由引理5可知,當條件(A1)成立時,線性特征值問題

的第1個特征值λ1是大于0的,并且λ1所對應的特征函數φ1為正.

下面敘述一個關于參數化非線性算子方程正解集合的全局結構.此結果為Dancer全局分歧定理[11]的推論.

假設E為一個實Banach空間,其上范數為‖·‖.令K?E為一個錐,若A([0,∞)×K)?K，則稱非線性映射A:[0,∞)×K→E是正的.若算子A連續,并且把[0,∞)×K中的有界子集映為E中的相對緊集，則稱上述非線性映射A為K-全連續的.最后,對于定義在E上的連續線性算子B,用r(B)表示算子B的譜半徑.

引理6[11]假設

(ii)A:[0,∞)×K→E為K-全連續的正算子.對任意的λ∈R,有A(λ,0)=0;對任意的u∈K,有A(0,u)=0,且

A(λ,u)=λBu+F(λ,u),

其中B:E→E為定義在E上的強正線性緊算子且滿足r(B)>0,F:[0,∞)×K→E滿足:當‖u‖→0時,‖F(λ,u)‖=o(‖u‖)對λ局部一致成立.

則存在

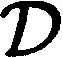
u≠0}∪{(r(B)-1,0)}

的一個無界連通子集C,使得(r(B)-1,0)∈C.

2 主要結果及其證明

定理1 設(A1)和(A2)成立,λ1=(r(T))-1.若

f∞<λ1

(10)

或

f0<λ1

(11)

成立,則奇異邊值問題(2)至少有1個正解.

注2 定理1中充分性條件(10)、(11)與奇異邊值問題(2)對應的線性問題的第1個特征值建立起了聯系.

注3 條件(10)、(11)中涉及的值λ1是最優的.若f∞=λ1=f0或f0=λ1=f∞,則奇異邊值問題(2)正解的存在性不能保證.考慮如下邊值問題:

u″(t)+a(t)u′(t)+b(t)u(t)+λ1u(t)+

ρ(u(t))=0,t∈(0,1),

(12)

u(0)=u(1)=0,

(13)

其中,

證明 僅給出式(10)成立時的證明，式(11)可類似證得.

為了研究問題(2)正解的存在性,考慮以下參數化問題：

(14)

令

f(t,s)=f0s+ξ(t,s),f(t,s)=f∞s+ζ(t,s).

(15)

則

(16)

于是,參數化問題(14)可重寫為

(17)

對空間Eu0以及其上的錐K，有

此閉包在u0-范數‖·‖u0下取得.事實上,設u∈Eu0，則存在常數l>0，使得

-l[t(1-t)]≤u(t)≤l[t(1-t)],t∈[0,1].

-(1+ρl)[t(1-t)]≤[t(1-t)±ρu(t)]≤

(1+ρl)[t(1-t)],t∈[0,1],

(18)

[t(1-t)±ρu(t)]≥(1-ρl)[t(1-t)]≥0,

t∈[0,1],

(19)

令u0(t)=t(1-t),t∈[0,1].則由式(18)和(19),有

u0±ρu∈K.

令

則u1,u2∈K,且滿足

u=u1-u2,

即u∈K-K,從而有

另一方面,由空間(Eu0,‖·‖u0)的完備性(見引理4),可推得

u=A(μ,u),

(20)

其中，

A(μ,u)=μBu+F(μ,u),

而

‖F(μ,u)‖u0=o(‖u‖u0)

令

Φ+:={u∈C[0,1]:u(t)>0,t∈[0,1],

u(0)=u(1)=0}.

(21)

f∞<λ1

即

可推得當μ=1時,問題(14)即原問題(2)至少有1個正解u存在.

假設(ηk,yk)∈C+,并且滿足|ηk|+‖yk‖∞→∞,k→∞.下面分2步來證明.

第1步 證明{ηk}有界.

反設ηk→∞,k→∞.則易證yk在區間[0,1]上變號.事實上,由(ηk,yk)∈C+有

(22)另一方面,由假設(A2)可知，存在e∈C[0,1],e(t)>0,t∈[0,1],使得

由上述事實以及ηk→∞,k→∞的假設可得

于是,由Sturm比較定理可知，對充分大的k,yk在區間[0,1]中至少有1個零點,這與yk>0矛盾!因此,{ηk}是有界的.進一步,由連通分支C+的無界性，可知‖yk‖∞→∞,k→∞.

由式(15)以及(ηk,yk)∈C+，知(ηk,yk)(k∈N)也滿足

(23)

令

則式(23)可變為

(24)

易知式(24)等價于

(25)

令

因為f(t,yk(t))=f∞yk(t)+ζ(t,yk(t)),所以由式(16)以及事實yk(t)>0,t∈[0,1]可推知:

這意味著存在一個不依賴于k的函數σ∈C[0,1],使得

于是{wk(t)}(k∈N)在C[0,1]中一致有界.并且,不難驗證

由C1[0,1]緊嵌入C[0,1]，說明存在vk的子列(不妨仍記為vk),使得對某個v*∈C[0,1]及η*∈[0,∞),有vk→v*且ηk→η*(k→∞).對式(25)運用Lebesgue控制收斂定理可得

上式蘊含了v*∈C2[0,1],且滿足

于是,

由定理1易得如下推論.

推論1 設(A1)和(A2)成立,λ1=(r(T))-1.若以下兩條件之一成立:

則奇異特征值問題

至少有1個正解.

定理2 設(A1)和(A2)成立,λ1=(r(T))-1.若以下兩條件之一成立:

(i)f0>λ1,f∞>λ1,且存在η*>0,使得f(t,u)

(ii)f0<λ1,f∞<λ1,且存在λ*>0,使得f(t,u)>B*λ*,(t,u)∈[0,1]×[0,λ*],

其中，

則奇異問題(2)至少有2個正解u1,u2.

證明 僅給出(i)成立時的證明.(ii)可類似證得.

由定理1的證明知,參數化問題

設(μ,u)∈C+,且滿足‖u‖∞=η*.則有

0

(26)

因此,由式(26)和條件(i)可得

f(t,u(t))

(27)

由引理2的(ii)以及式(27),對滿足‖u‖∞=η*的(μ,u)有

從而,對滿足‖u‖∞=η*的(μ,u)一定有

μ>1.

又由假設條件(i)可得

(1,u1),(1,u2)∈C+,

且滿足‖u1‖∞<η*,‖u2‖∞>η*,即問題(2)有2個正解.定理證畢.

[1]O’REGAND.SingularDirichletboundaryvalueproblemsI.Superlinearandnonresonantcase[J]. Nonlinear Analysis,1997,29:221-245.

[2] ASAKAWA H. Nonresonant singular two-point boundary value problems [J]. Nonlinear Analysis,2001,44:791-809.

[3] XU X, MA J P. A note on singular nonlinear boundary value problems [J]. J Math Anal Appl,2004,293:108-124.

[4] HAN G D, WU Y. Nontrivial solutions of singular two-point boundary value problems with sign-changing nonlinear terms [J]. J Math Anal Appl,2007,325:1327-1338.

[5] DALMASSO R. Positive solutions of singular boundary value problems [J]. Nonlinear Analysis,1996,27:645-652.

[6] AGARWAL R P, WONG F H, LIAN W C. Positive solutions for nonlinear singular boundary value problems [J]. Appl Math Letters,2002,130(2/3):225-234.

[7] HA K S, LEE Y H. Existence of multiple positive solutions of singular boundary value problems [J]. Nonlinear Analysis,1997,28(8):1429-1438.

[8] LI J M, WANG J X. Triple positive solutions for a type of second-order singular boundary problems [J]. Boundary Value Problems,2010,2010(1):1-14.

[9] MA R Y, THOMPSON B. Multiplicity results for second-order two-point boundary value problems with superlinear or sublinear nonlinearities [J]. J Math Anal Appl,2005,303:726-735.

[10] MA R Y. Global behavior of the components of nodal solutions of asymptotically linear eigenvalue problems [J]. Applied Mathematics Letters,2008,21:754-760.

[11] DANCER E. Global solution branches for positive mappings [J]. Arch Rat Mech Anal,1973,52:181-192.

[12] ZEIDLER E. Nonlinear Functional Analysis and Its Applications, I. Fixed-Point Theorems[M]. New York: Springer-Verlag,1985.

[13] DEIMLING K. Nonlinear Functional Analysis[M]. New York: Springer-Verlag,1985.

[14] GUO D, LAKSHMIKANTHAM V. Nonlinear Problems in Abstract Cones[M]. New York: Academic Press,1988.

YANDongming

(School of Mathematics and Statistics, Zhejiang University of Finance and Economics, Hangzhou 310018, China)

Existenceofsingleandmultiplepositivesolutionsofsingularboundaryvalueproblem.

singularboundaryvalueproblem;globalbifurcation;positivesolutions;multiplepositivesolutions;firsteigenvalue

2015-01-04.

浙江省教育廳一般項目(Y201534471).

閆東明(1982-),ORCID:http://orcid.org/0000-0002-2893-4871，男，博士，講師，主要從事微分方程研究,E-mail:13547895541@126.com.

10.3785/j.issn.1008-9497.2017.03.006

O

A

1008-9497(2017)03-281-07