Multiplicatively weighted Harary indexof some graph operations

WEN Yanqing, LIU Baoliang, AN Mingqiang

(1.College of Mathematics and Computer Science, Shanxi Datong University, Datong 037009, Shanxi Province, China;2.College of Science, Tianjin University of Science and Technology, Tianjin 300457, China)

Multiplicatively weighted Harary indexof some graph operations

WEN Yanqing1, LIU Baoliang1, AN Mingqiang2*

(1.College of Mathematics and Computer Science, Shanxi Datong University, Datong 037009, Shanxi Province, China;2.College of Science, Tianjin University of Science and Technology, Tianjin 300457, China)

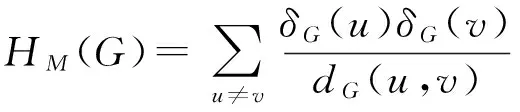
multiplicativelyweightedHararyindex;Hararyindex;tensorproduct;strongproduct;wreathproduct

0 Introduction

Allgraphsconsideredinthispaperarefiniteundirectedsimpleconnectedgraphs.LetG=(V(G),E(G)) be a graph with vertex setV(G) and edge setE(G). LetδG(v) be the degree of a vertexvinGanddG(u,v) be the distance between two verticesuandvinG. When the graph is clear from the context, we will omit the subscriptGfrom the notation. For other undefined terminology and notations from graph theory, the readers are referred to[1].

A topological index is a number related to a graph invariant under graph isomorphism. Obviously, the number of vertices and edges of a given graphGare topological indices ofG. One of the oldest and well-studied distance-based topological index is the Wiener numberW(G), also termed as Wiener index in chemical or mathematical chemistry literature, which is defined as the sum of distances over all unordered vertex pairs inG[2], namely,

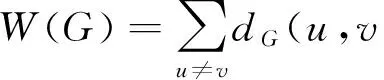
ThisformulawasintroducedbyHOSOYA[3],althoughtheconcepthasbeenintroducedbylaterWIENER.However,theapproachbyWIENERisapplicableonlytoacyclicstructures,whilstHOSOYA’SmatrixdefinitionallowedtheWienerindextobeusedforanystructure.

Anotherdistance-basedgraphinvariant,definedby[4-5]inafullyanalogousmannertoWienerindex,istheHararyindex,whichisequaltothesumofreciprocaldistancesoverallunorderedvertexpairsinG, that is,

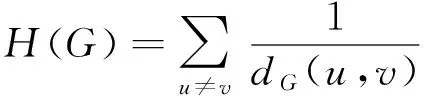
In1994,DOBRYNINetal[6]andGUTMAN[7]independentlyproposedavertex-degree-weightedversionofWienerindexcalleddegreedistanceorSchultzmoleculartopologicalindex,whichisdefinedforagraphGas

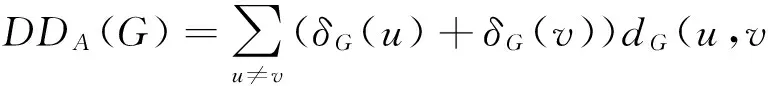
Similarly,theGutmanindexisputforwardin[7]andcalledtheretheSchultzindexofthesecondkind,forwhichthenameGutmanindexhasalsosometimesbeenused[8].Itisdefinedas

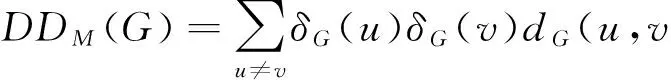
Theinterestedreadersmayconsult[9-11]forWienerindex, [5]forHararyindex, [12-13]fordegreedistanceand[14-15]forGutmanindex.

AlthoughHararyindexisnotwellknowninthemathematicalchemistrycommunity,itarisesinthestudyofcomplexnetworks.Letndenote the number of vertices ofG. DividingH(G) byn(n-1), we obtain a normalization ofH(G), which is called the efficiency ofG[16]. The reciprocal value of the efficiency is called the performance ofG[17]. For a given network, both efficiency and performance afford a uniform way to express and quantify the small-world property. Since the strength of interactions between nodes in a network is seldom properly described by their topological distances, one needs to consider both the weighted versions of efficiency and performance.

In order to close the gap between the two research communities by drawing their attention to a generalization of a concept, which gives more weight to the contributions of pairs of vertices of high degrees. Recently, ALIZADEH et al[18]introduced an invariant, named additively weighted Harary index, which is defined as

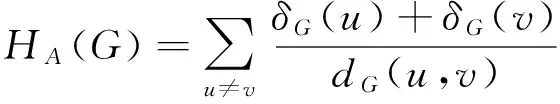
Somebasicmathematicalpropertiesofthisindexwereestablished[18]andtheirbehaviorunderseveralstandardgraphproductswereinvestigatedthere.

Itisknownthattheintuitiveideaofpairsofcloseatomscontributingmorethanthedistantonesisdifficulttocaptureintopologicalindices.Apossiblyusefulapproachcouldbeusedtoreplacetheadditiveweightingofpairsbythemultiplicativeone,thusgivingrisetoanewinvariant,namedmultiplicativelyweightedHararyindex[18]:

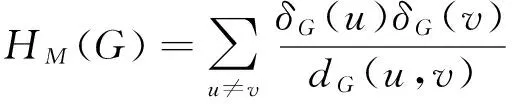
Evidently,theadditively(resp.multiplicatively)weightedHararyindexisrelatedtotheHararyindexinthesamewayasthedegreedistance(resp.Gutmanindex)isrelatedtotheWienerindex.

Veryrecently,PATTABIRAMANetal[19]gavetheexactformulaefortheadditivelyweightedHararyindexoftensorproductG×Km0,m1,…,mr-1and the strong productGKm0,m1,…,mr-1, whereKm0,m1,…,mr-1is the complete multipartite graph with partite sets of sizesm0,m1,…,mr-1.

In this paper, we continue this program to the multiplicatively weighted Harary index, and the exact formulae for the multiplicatively weighted Harary index of tensor productG×Kr, the strong productG□×Krand the wreath productG1°G2in terms of other graph invariants including additively weighted Harary index, Harary index, the first and the second Zagreb indices, and the first and the second Zagreb coindices, are obtained, whereKris the complete graph. Additionally, we apply our results to compute the multiplicatively weighted Harary index of open fence and closed fence graphs.

The paper is organized as follows. In section 1, we give some necessary definitions. In section 2 to 4, we present our main results and give some corresponding examples, respectively.

1 Preliminaries

1.1 Some definitions

For a given graphG, its first and second Zagreb indices are defined as follows:

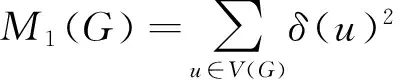
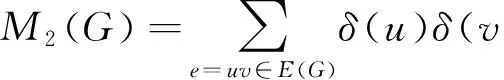
ThefirstZagrebindexcanbealsoexpressedasasumoveredgesofG,

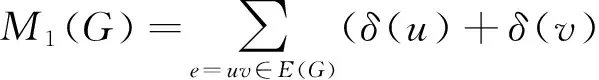
FortheproofofthisfactandmoreinformationonZagrebindices,weencouragetheinterestedreaderto[20].

ThefirstandthesecondZagrebcoindicesofagraphGare defined as follows[21]:

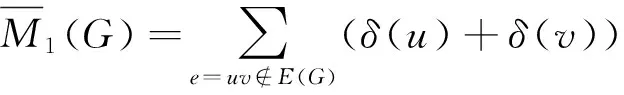
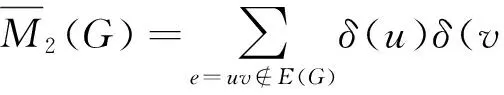
LetKn,CnandPndenote then-vertex complete graph, cycle and path, respectively. We callC3a triangle.

1.2 Product graphs

Now, we introduce three standard types of product graphs that we consider in this paper. For two simple graphsGandH, their tensor product denoted byG×H, has vertex setV(G)×V(H) in which (g1,h1) and (g2,h2) are adjacent wheneverg1g2is an edge inGandh1h2is an edge inH. Note that ifGandHare connected graphs, thenG×His connected only if at least one of the graph is nonbipartite. The strong product of graphsGandH, denoted byG□×H, is the graph with vertex setV(G)×V(H)={(u,v):u∈V(G),v∈V(H)} and (u,x)(v,y) is an edge whenever (i)u=vandxy∈E(H), or (ii)uv∈E(G) andx=y, or (iii)uv∈E(G) andxy∈E(H). Similarly, the wreath product (also known as the composition) of the graphsGandH, denoted byG°H, has vertex setV(G)×V(H) in which (g1,h1)(g2,h2) is an edge wheneverg1g2∈E(G), org1=g2andh1h2∈E(H). The tensor product of graphs has been extensively studied in relation to the areas such as graph colorings, graph recognition, decompositions of graphs, and design theory, see [22-26].

For more information about graph products, please see monograph[25]. There is a growing corpus of literature concerned with the study of graph invariants of tensor product, Cartesian product and strong product[27-29].

2 Multiplicatively weighted Hararyindex of tensor product of graphs

LetGbe a connected graph withV(G)={v0,v1,…,vn-1} andV(Kr)={u1,u2,…,ur-1}. For convenience, letxijdenote the vertex (vi,uj) ofG×Kr. The following lemma, which follows easily from the properties and structure ofG×Kr, is used in the proof of our main result in this section.

Lemma 1 LetGbe a connected graph onn≥2 vertices andxij,xkpbe any pair vertices of the graphG′=G×Kr, wherer≥3.

(i)Ifvivk∈E(G), then

dG′(xij,xkp)=

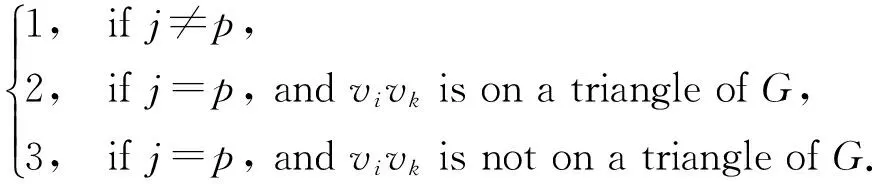
(ii)Ifvivk?E(G), thendG′(xij,xkp)=dG(vi,vk).

(iii)dG′(xij,xip)=2.

Lemma 2 LetGbe a connected graph and letG′=G×Kr. Then the degree of a vertex (vi,uj) inG′ isδG′((vi,uj))=δG(vi)(r-1).

Now, we present the exact formulae for the multiplicatively weighted Harary index ofG×Kr.

Theorem 1 LetGbe a connected graph withn≥2 vertices andE2be the set of edges ofGwhich do not lie on any triangle of it. Then

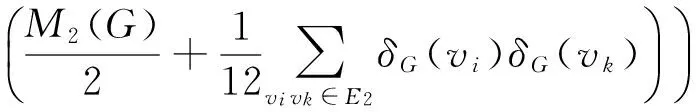
wherer≥3.

Proof Let us denoteG′=G×Kr. Obviously,

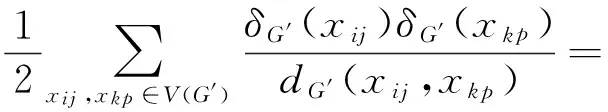
(1)

whereA1toA3are the sums of the above terms, in order. In what follows, we computeA1toA3of (1), separately.

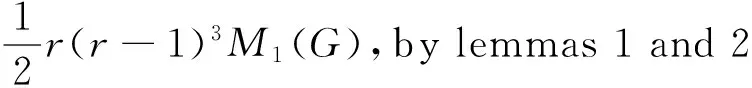
(2)

To do this, originally we calculate

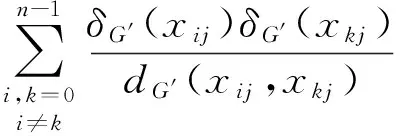
LetE1={uv∈E(G)|uvis on a triangle ofG} andE2=E(G)-E1.

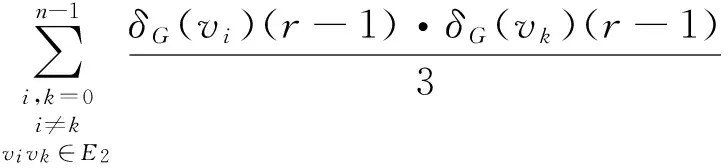
by lemmas 1 and 2,

The above formula=

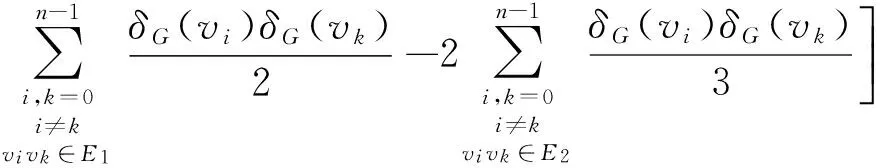
sincedG(vi,vk)=1,ifvivk∈E1andvivk∈E2,

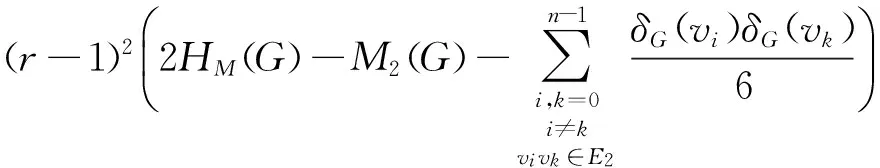
(3)

since each edgevivkofGis being counted twice in the sum, that is,vivkandvkvi.

Now summing (3) overj=0,1,…,r-1, we have

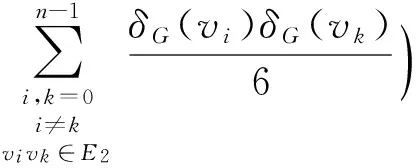
(4)

2r(r-1)3HM(G), by lemmas 1 and 2.

(5)

Combining(2), (4) and (5) with (1), we obtain

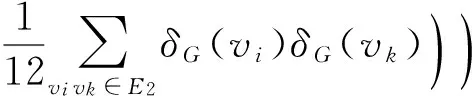
By theorem 1, we have the following corollaries.

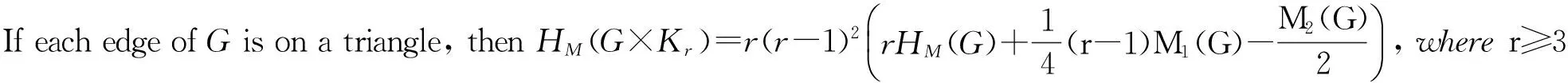
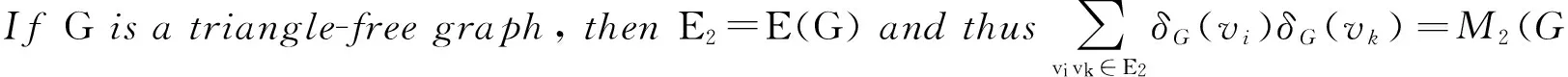
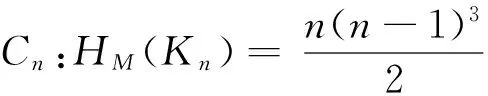
Combiningtheaboveknownresultsandcorollaries1and2,immediately,wecanobtaintheexplicitmultiplicativelyweightedHararyindexofthefollowinggraphs:

Example 1

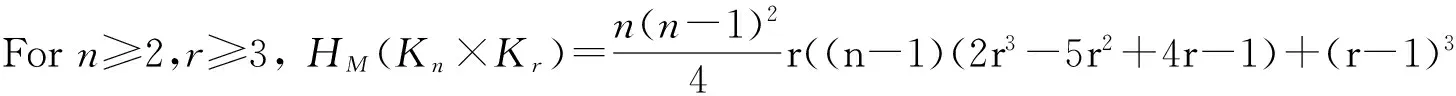
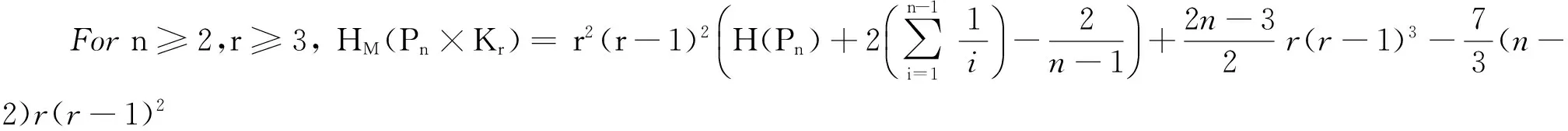
(c)Forn≥2,r=3,HM(Cn×Kr)=3r(5r3-13r2+11r-3).

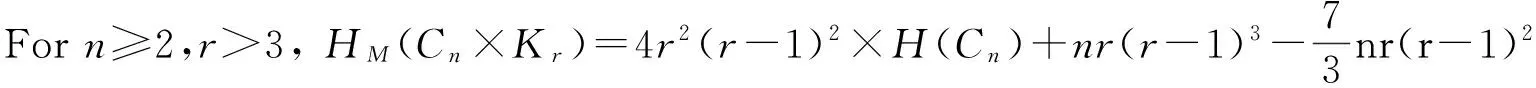
3 Multiplicatively weighted Hararyindex of strong product of graphs

In this section, we obtain the multiplicatively weighted Harary index ofG□×Kr. LetGbe a connected graph withV(G)={v0,v1,…,vn-1} andV(Kr)={u1,u2,…,ur-1}. For convenience, letxijdenote the vertex (vi,uj) ofG□×Kr. Firstly, we give the following lemma, which follows directly from the properties and structure ofG□×Kr, is used in the proof of our main result in this section.

Lemma 3 LetGbe a connected graph and letG′=G□×Kr. Then

(i)For any pair of verticesxij,xkp∈V(G′),dG′(xij,xip)=1 anddG′(xij,xkp)=dG(vi,vk).

(ii)The degree of a vertex (vi,uj) inG′ isδG′((vi,uj))=rδG(vi)+(r-1).

Theorem 2 LetGbe a connected graph withnvertices andmedges. Then

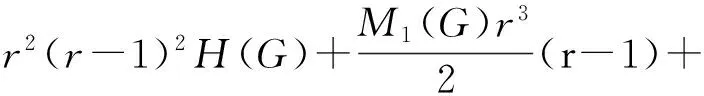
Proof Let us denoteG′=GKr. Obviously,

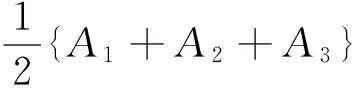
(6)

whereA1,A2andA3are the sums of the above terms, in order.

In what follows, we calculateA1,A2andA3of (6), separately.

2r(r-1)δG(vi))=

r3(r-1)M1(G)+nr(r-1)3+

4mr2(r-1)2,by lemma 3.

(7)

2r3HM(G)+2r2(r-1)HA(G)+

2r(r-1)2H(G).

(8)

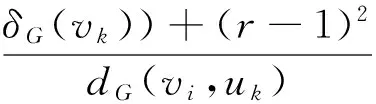
2r3(r-1)HM(G)+2r2(r-1)2HA(G)+

2r(r-1)3H(G).

(9)

Combining (7)～(9) with (6), we get

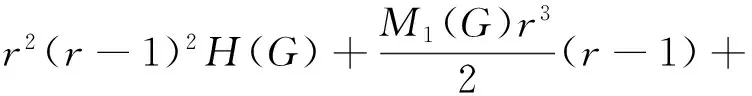
Asanapplication，wepresentformulaeformultiplicativelyweightedHararyindexofopenandclosedfences,Pn□×K2andCn□×K2.

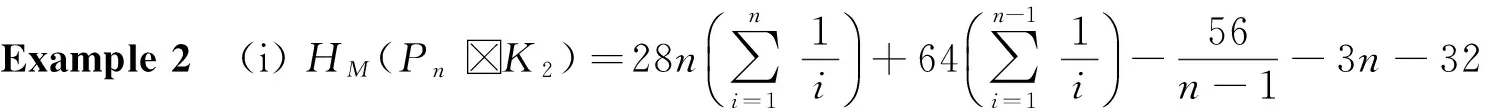
4 Multiplicatively weighted Hararyindex of wreath product of graphs

In this section, we give the multiplicatively weighted Harary index ofG1°G2. LetG1andG2be two connected graphs withV(G1)={v0,v1,…,vn1-1} andV(G2)={u0,u1,…,un2-1}. For convenience, letxijdenote the vertex (vi,uj) ofG1°G2. The following lemma, which follows easily from the properties and structure ofG1°G2, is used in the proof of our main result in this section.

Lemma 4 LetG1andG2be two connected graphs and letG′=G1°G2. Then the degree of a vertex (vi,uj) inG′ isδG′((vi,uj))=n2δG1(vi)+δG2(uj).

Theorem 3 LetG1andG2be two connected graphs. The number of vertices and edges of graphGiis denoted byniandeirespectively fori=1,2. Then we have

H(G1)(M1(G2)+2M2(G2)+

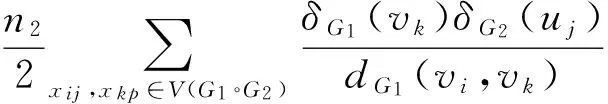
Proof Let us denoteG′=G1°G2. Obviously,

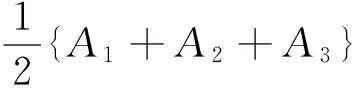
(10)

whereA1toA3are the sums of the above terms, in order.

In what follows, we computeA1,A2,A3of (10), separately.

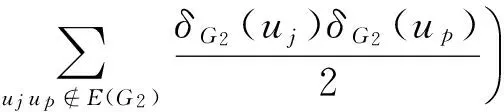
since each row induces a copy ofG2and

dG′(xij,xip)=1 ifujup∈E(G2) and

dG′(xij,xip)=2 ifujup?E(G2).

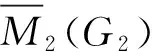
(11)

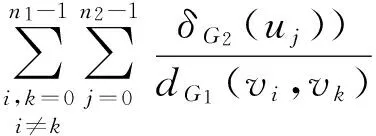
since the distance between a pair of vertices in a column is the same as the distance between the corresponding vertices of other column.

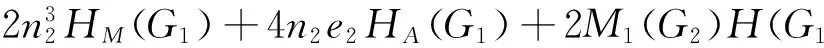
(12)

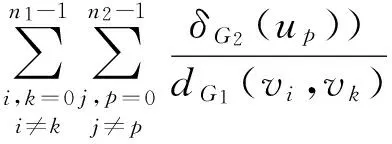
sincedG′(xij,xkp)=dG1(vi,vk) for alliandk, and further the distance between the corresponding vertices of the layers is counted inA2,

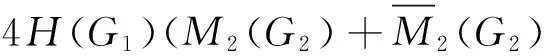
(13)

Combining (11)～(13) with (10), we get the desired result.

This completes the proof.

Using theorem 2, we have the following corollary.

Corollary 3 LetG1be a connected graph andG2be a connectedk-regular graph. The number of vertices and edges of graphGiis denoted byniandeirespectively fori=1,2. Then, we have

2e2)HA(G1)+H(G1)(M1(G2)+

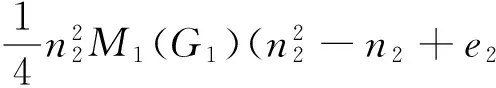
[1] BONDY J A, MURTY U S R. Graph Theory with Applications, Macmillan[M]. London: Elsevier, 1976.

[2] WIENER H. Structural determination of paraffin boiling point[J]. J Amer Chem Soc,1947,69:17-20.

[3] HOSOYA H. A newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons[J]. Bull Chem Soc Jpn,1971,44:2332-2339.

[4] IVANCIUC O, BALABAN T S, BALABAN A T. Reciprocal distance matrix, related local vertex invariants and topological indices[J]. J Math Chem,1993(12):309-318.

[6] DOBRYNIN A A, KOCHETOVA A A. Degree distance of a graph: A degree analogue of the Wiener index[J]. J Chem Inf Comput Sci,1994,34:1082-1086.

[7] GUTMAN I. Selected properties of the Schultz molecular topogical index[J]. J Chem Inf Comput Sci,1994,34:1087-1089.

[8] TODESCHINI R, CONSONNI V. Handbook of Molecular Descriptors[M]. Weinheim:Wiley-VCH,2000.

[9] DOBRYNIN A A, ENTRINGER R, GUTMAN I. Wiener index of trees: Theory and applications[J]. Acta Appl Math,2001,66:211-249.

[10] GUTMAN I. A property of the Wiener number and its modifications[J]. Indian J Chem A,1997,36:128-132.

[11] GUTMAN I, RADA J, ARAUJO O. The Wiener index of starlike trees and a related partial order[J]. Match Commun Math Comput Chem,2000,42:145-154.

[13] TOMESCU I. Ordering connected graphs having small degree distances[J]. Discrete Appl Math,2010,158:1714-1717.

[14] FENG L, LIU W. The maximal Gutman index of bicyclic graphs[J]. MATCH Commun Math Comput Chem, 2011,66:699-708.

[15] MUKWEMBI S. On the upper bound of Gutman index of graphs[J]. MATCH Commun Math Comput Chem,2012,68:343-348.

[16] LATORA V, MARCHIORI M. Efficient behavior of small-world networks[J]. Phys Rev Lett,2001,87:198701.

[17] MARCHIORI M, LATORA V. Harmony in the small-world[J]. Physica A, 2000,285:539-546.

[18] ALIZADEH Y, IRANMANESH A, DOT. Additively weighted Harary index of some composite graphs[J]. Discrete Math, 2013,313:26-34.

[19] PATTABIRAMAN K, VIJAYARAGAVAN M. Reciprocal degree distance of product graphs[J]. Discrete Appl Math, 2014,179:201-213.

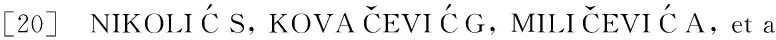
[22] ALON N, LUBETZKY E. Independent set in tensor graph powers[J]. J Graph Theory, 2007,54:73-87.

[23] ASSAF A M. Modified group divisible designs[J]. Ars Combin, 1990,29:13-20.

[25] IMRICH W, KLAV?AR S. Product Graphs: Structure and Recognition[M]. New York, John Wiley and Sons,2000.

[26] MAMUT A, VUMAR E. Vertex vulnerability parameters of Kronecker products of complete graphs[J]. Inform Process Lett,2008,106:258-262.

[27] HOJI M, LUO Z, VUMAR E. Wiener and vertex PI indices of Kronecker products of graphs[J]. Discrete Appl Math,2010,158:1848-1855.

[28] KHALIFEH M H, YOUSERI-AZARI H, ASHRAFI A R. Vertex and edge PI indices of Cartesian product of graphs[J]. Discrete Appl Math,2008,156:1780-789.

[29] PATTABIRAMAN K, PAULRAJA P. On some topological indices of the tensor product of graphs[J]. Discrete Appl Math,2012,160:267-279.

倍乘賦權(quán)Harary指標(biāo);Harary指標(biāo); 張量積; 強(qiáng)積; 圈積

O

A

1008-9497(2017)03-253-09

Foundation item:Supported by the Doctoral Scientific Research Foundation of Shanxi Datong University (2015-B-06).

10.3785/j.issn.1008-9497.2017.03.001

Received date：October 16,2015.

About the author:WEN Yanqing(1980-),ORCID:http://orcid.org/0000-0002-9573-7245,female, doctoral student, lecture, the field of interest are reliability and graph theory, E-mail:oryqwen@163.com.

*Corresponding author, ORCID:http://orcid.org/0000-0002-1105-750X,E-mail:anmq@tust.edu.cn.

溫艷清1, 劉寶亮1, 安明強(qiáng)2(1.山西大同大學(xué) 數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院, 山西 大同 037009; 2. 天津科技大學(xué) 理學(xué)院，天津 300457)

若干運(yùn)算圖的倍乘賦權(quán)Harary指標(biāo).浙江大學(xué)學(xué)報(bào)(理學(xué)版),2016,44(3):253-260，280