一道圓錐曲線題目引發的思考
西華師范大學(637000) 寇唯煒●
?
一道圓錐曲線題目引發的思考
西華師范大學(637000)
寇唯煒●
圓錐曲線的定值問題一直都是高考的熱點問題.從四川省雙流中學2014級高三九月月考21題(2)問證明得到的結論,將其進行了深入推廣.研究了過焦點的直線與準線的交點,及與圓錐曲線的交點這三點和圓錐曲線上橫坐標等于焦點的橫坐標的點所成斜率的關系.
圓錐曲線,斜率,定值
一、問題再現


(1)求橢圓C的方程.
(2)AB是經過右焦點F的任一弦(不經過點P),設直線AB與l相交于點M,記PA,PB,PM的斜率分別為k1,k2,k3,問:是否存在常數λ,使得k1+k2=λk3?若存在,求出λ的值;若不存在,說明理由.

(2)設lAB:y=k(x-1) ①.

整理得(3+4k2)x2-8k2x+4k2-12=0.
設A(x1,y1),B(x2,y2),
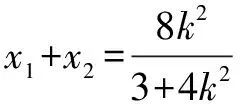
將x=4代入①得M(4,3k),





此題是以橢圓為載體,通過直線與圓錐曲線的位置關系,設而不求等相關知識,同時考查了學生的探究能力,將此結論推廣到雙曲線和拋物線中發現也能得到同樣的結果.



化得(b2-a2k2)x2+2a2k2cx-(a2k2c2+a2b2)=0.
設A(x1,y1),B(x2,y2) ①,






將②③對比得k1+k2=2k3.

證明 設拋物線為:y2=2px,






∵A,F,B三點共線,


由①代入得k1+k2=2k+2 ③.
將②③對比得k1+k2=2k3
以上的探究證明,知道對于中心(頂點)在坐標原點的三種圓錐曲線(平面內到定點與定直線距離的比為常數e的點的軌跡)揭示了他們內在的本質聯系,都滿足圓錐曲線上當橫坐標為定值的點與過該點的直線與定直線和圓錐曲線的三個交點構成直線的斜率關系.圓錐曲線內在的和諧統一決定了它們還有更多優美的性質等待我們去探究與挖掘.
[1]陸應海.“有心”圓錐曲線焦點弦的一個優美定理與推論[J].
G632
B
1008-0333(2017)10-0047-02

